 |
Wer Übungsaufgabe 3.3-1
gemacht oder zumindest angeschaut hat, ist über ein gewisses Sprachproblem gestolpert: Es wird eine "Raumdiagonalebene" eingeführt, und auch sonst werden Ebenen
in einem Gitter/Kristall prominent herausgestellt. |
|
 |
Wenn man nicht beschreibend bleiben will ("die Ebene, die beim Atom oben
links beginnt und durch die Atome ... führt"), gibt man sich am besten eine mathematische Definition, die alle
möglichen Fälle einschließt. Man macht das überall auf der Welt mit den sogenannte Miller-Indizes,
die wie folgt definiert sind: |
|
|
| Definition (und Rezept) |
Eine Ebene in einem Gitter wird durch drei ganze Zahlen indiziert, indem man
|
- den Ursprung der EZ
nicht in die zu indizierende Ebene legt, sondern in eine Nachbarebene;
- die Schnittpunkte der Ebene mit den Basisvektoren bestimmt (wenn kein Schnittpunkt
vorhanden ist, entspricht das "¥ ");
- das erhaltene Zahlentripel reziprok
darstellt und die resultierenden Brüche durch Erweitern ganzzahlig macht; aus ¥
wird dabei 0. Nicht erlaubt ist Kürzen, falls die reziproken Zahlen keine
Brüche sind (aus den Schnittpunkten 1/2, 1/2, 1/2 erhält man 2, 2, 2 und nicht 1, 1, 1).
- Auftauchende negative Zahlen werden durch einen Überstrich dargestellt (in HTML nicht so einfach darstellbar, wir schreiben stattdessen mit '-Zeichen)
- Das Zahlentripel hkl wird in runde Klammern (hkl) gesetzt, falls es sich um eine spezifische
Ebene handelt, und in
geschweifte Klammern {hkl}, falls die Gesamtheit aller kristallographisch
gleichwertigen Ebenen mit denselben Indizes gemeint ist.
|
|
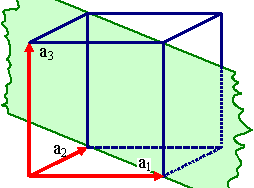 |
Kubisches Gitter
Schnittpunkte bei
1, 1,
¥
Indizes (110) |
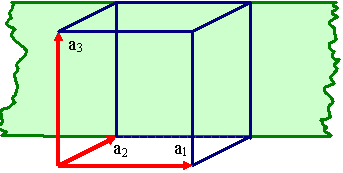 |
Kubisches Gitter
Schnittpunkte bei
¥ , 1, ¥
Indizes (010) |
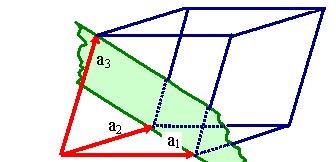 |
Triklines Gitter
Schnittpunkte bei
1, 1, 1
Indizes (111) |
|
|
 |
Das mag zunächst etwas verquer erscheinen - es ist aber ungeheuer nützlich, denn
mit den so gewonnenen Zahlen (= Miller-Indizes) läßt sich famos rechnen! |
 |
Wenn wir schon dabei sind, definieren wir gleich noch die Miller-Indizes für Richtungen: |
|
|
| Definition (und Rezept) |
Eine Richtung
in einem Gitter wird durch drei ganze Zahlen
indiziert, indem
|
- der Ursprung der EZ auf die gewünschte Richtung gelegt wird;
- ein Vektor in der gewünschten Richtung in kleinstmöglichen ganzzahligen Komponenten der Basisvektoren ausgedrückt
wird;
- auftauchende negative Zahlen durch einen Überstrich darstellt werden (in HTML nicht so leicht
darstellbar, wir schreiben stattdessen mit dem Minus ["–"] oder Strich [" ' "]) und
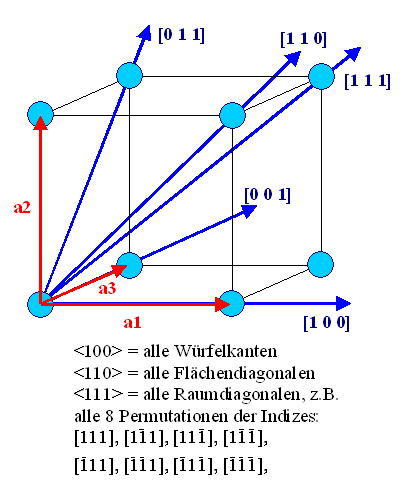
- das erhaltene Zahlentripel uvw in eckige Klammern
[uvw] gesetzt wird, wenn es sich um eine spezifische Richtung handelt, und in
spitze Klammern <uvw>, wenn die Gesamtheit aller
kristallographisch gleichwertigen Richtungen gemeint ist.
|
|
 |
|
 |
Das müssen wir üben! |
| |
|
|
Rechnen mit Miller-Indizes |
| |
|
 |
Wir können bereits hier einige Vorteile (aber noch längst nicht alle)
der auf den ersten Blick etwas seltsamen Miller-Indizes ableiten und verwenden. Im folgenden sind sie für kubische Gitter nur postuliert und aufgelistet; die Ableitungen
und Beweise schenken wir uns hier. Wer's genauer wissen will, benutzt den Link. |
|
 |
1. Die Richtung [hkl] steht immer senkrecht
auf der Ebene (hkl). |
|
 |
2. Die Abstände
dhkl zwischen zwei direkt benachbarten Gitterebenen sind direkt aus den Indizes berechenbar. Die
Formeln für nichtkubische Gittersysteme können
etwas kompliziert sein, aber in unseren kubischen Gittern gilt ganz einfach:
|
| |
| dhkl = | a
(h2 + k2 + l2)1/2
|
|
|
|
 |
Damit wird klarer, warum die gewählte "reziproke" Definition der Miller-Indizes für
Ebenen sehr vorteilhaft ist. |
 |
Damit haben wir aber die Thematik "Rechnen mit Miller-Indizes" nur gestreift. Sobald
man zum Beispiel Röntgenstruktruranalytik betreibt, d.h. aus Röntgenbeugungsmessungen den Kristall rekonstruieren
will, wird man heftigst mit Miller-Indizes hantieren. |
| |
|
© H. Föll (MaWi für ET&IT - Script)



