5. Grundzüge von Thermodynamik und Statistik

5.1 System, Temperatur, Energie und Entropie

5.1.1 Was ist ein System oder Ensemble?

Systeme und erste Schlußfolgerungen

Thermodynamik im Wortsinn hat was mit Temperatur und Dynamik zu tun. Das Wort "Temperatur " impliziert, daß wir ein Ensemble oder System betrachten, das Wort "Dynamik" impliziert, daß sich im betrachteten System etwas ändert.

Bevor wir uns Begriffen wie Temperatur oder gar "Entropie" näher zuwenden, definieren wir erst mal, was genau ein "System" ist. In der harten Physik benutzt man gern das Wort "Ensemble" statt System und macht noch ein paar Fallunterscheidungen, wir verwenden ab jetzt aber nur noch den Ausdruck "System" ohne weitere Differenzierung.

Im folgenden wird der gelernte Physiker oder Materialwissenschaftler deshalb viele Ungenauigkeiten oder "eigentlich" unzulässige Vereinfachungen finden. Sei's drum. Wir machen hier "Thermodynamik" nicht, weil es so eine tolle Wissenschaft ist (ist sie!), sondern nur, um die allernotwendigsten Begriffe kennenzulernen, die man für Halbleiter usw. unbedingt braucht.

Was ist ein thermodynamisches System? Soweit es uns betrifft, reicht die folgende Definition:

Ein thermodynamisches System besteht aus einer großen Zahl von Teilchen, die miteinander in Wechselbeziehung in Form von Energieaustausch stehen.

Was bedeutet "große Zahl"? Nehmen wir als Beispiel ein makroskopisches Krümelchen, das wir so gerade noch sehen können, also ca. (0,1 mm)³ = 1 · 10¹⁵ nm³ groß. Ein Atom, das wissen wir jetzt, hat einen Radius in der Größenordnung von 0,1 nm und ist damit ca. 0,004 nm³ groß (Abschätzung via Kugelvolumen). In unserem kleinen Krümelchen stecken also rund und roh 2,5 · 10¹⁷ Atome – eine durchaus große Zahl.

Was wir uns ungefähr merken, ist die Avogadrokonstante N_A = Zahl der Teilchen in einem Mol = 6 · 10²³ mol^–1. (Das molare Volumen eines Stoffes ist das Volumen, das genau ein Mol des Stoffes enthält, d.h. N_A Teilchen.)

Statt diese Definition lange zu diskutieren, schauen wir uns drei Beispiele an, um uns noch den einen oder anderen Punkt zu verdeutlichen.

Wir betrachten insbesondere die innere Energie U, d.h. was energetisch noch bleibt, nachdem man äußere Energien, wie z.B. das Gravitationspotential oder die kinetische Energie, die allen Teilchen gemeinsam ist, abgezogen hat. In anderen Worten: Es ist uns gleichgültig ob unser Kristall bei Höhe Normalnull (= 0 m; mgh = 0 eV) sitzt, auf der Spitze des Mount Everest oder auf dem Mond, oder ob wir ihm mit dem Auto durch die Gegend fahren und damit ½mv²_Auto zusätzliche äußere Energie einbringen.

Die drei unten gezeigten Systeme sollen auch soweit geschlossen sein, daß sich die Zahl der beteiligten Teilchen nicht ändert. Das heißt schlicht, daß das Gas in einem Kasten eingesperrt ist und der Kristall eine feste Größe hat.

Gas	Kristall : Atome	Kristall: freie Elektronen
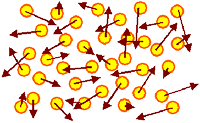
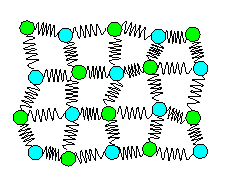
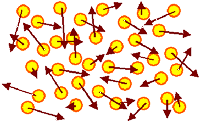
Ein (einatomiges) Gas	Ein Kristall	Ein "Elektronengas "
Die drei Systeme (bei der Temperatur T) in einer Momentanbetrachtung
Die Atome (oder auch Moleküle) fliegen mit konstanter Geschwindigkeit (angedeutet durch braune Pfeile) durch den verfügbaren Raum. Dies ist eine Momentaufnahme mit ganz kurzer Belichtungszeit. Wenige Mikroekunden später sehen die Pfeile überall anders aus, da sich durch Stöße die Geschwindigkeitsvektoren ständig ändern. Das neue Bild ist aber im Prinzip dem alten sehr ähnlich.	Die Atome schwingen in ihrem Potentialtopf (symbolisiert durch Federn) um die Gleichgewichtslage. Dies ist eine Momentaufnahme mit Bezug auf die Geschwindigkeiten mit ganz kurzer Belichtungszeit. Wenige Nanosekunden später sieht im Details alles anders, im Prinzip aber gleich aus.	Die Elektronen (oder auch "Löcher") fliegen mit konst. Geschwindigkeit (angedeutet durch braune Pfeile) durch den verfügbaren Raum. Dies ist eine Momentaufnahme mit ganz kurzer Belichtungszeit. Wenige Picosekunden später sehen die Pfeile überall anders aus, da sich durch Stöße die Vektoren ständig ändern. Das neue Bild ist aber im Prinzip dem alten sehr ähnlich.
Die drei Systeme im Zeitmittel
Die Summe der in den individuellen Bewegungen der Atome steckenden inneren Energie U = S½ mv² ist konstant. Damit kann man einem Atom (und auch Molekül unter Berücksichtigung möglicher Rotationsenergien) eine mittlere Energie zuordnen.	Die in der Schwingung der Atome steckende innere Energie U = S(U_pot + U_kin) ist konstant. Damit kann man einem Atom eine mittlere Energie zuordnen	Die "irgendwie" in den Elektronen steckende innere Energie U ist konstant.
Die Natur der beteiligten Teilchen
Die Atome / Moleküle im Gas darf man noch wie klassische "Massenpunkte" behandeln. Aus quantenmechanischer Sicht verhalten sie sich wie Bosonen , d.h. sie dürfen alle denselben Zustand (= Energie) haben	Die Atome im Kristall darf man bezüglich ihrer "Mechanik" noch wie klassische "Massenpunkte" an Federn behandeln. Aus quantenmechanischer Sicht verhalten sie sich wie Bosonen, d.h. sie dürfen alle denselben Zustand (= Energie) haben	Die Elektronen im Kristall unterliegen voll der Quantentheorie. Sie sind Fermionen, max. 2 (Spin "rauf" bzw. "runter") können denselben Zustand besetzen.
Verfügbare Zustände / Energien
Verfügbare Energien bilden ein Kontinuum, beginnend bei U = 0 eV, sinnvollerweise für die Geschwindigkeit v = 0 cm/s.	Verfügbare Energien bilden ein Kontinuum, beginned bei U = 0 eV, sinnvollerweise für die Schwingungsamplitude = 0 cm.	Die verfügbaren Zustände mit den zugehörigen Energien sind i.d.R. diskret; die Zustände sind i.d.R. bezüglich der Energie mehr oder weniger entartet (mehrer unterschiedliche Zusände haben dieselbe Energie). Die Zustände für die hier betrachteten "freien" Elektronen sind in Bändern angeordnet.

Erste Schlußfolgerung: Bei allen drei Systemen wird nach hinreichend langer Zeit (ns . . . ms) ein Gleichgewicht derart erreicht sein, daß folgendes gilt:

Überall (= in jedem Volumenelement dV >> Teilchengröße) ist die Situation im Mittel dieselbe, d.h. die Teilchen haben im Mittel dieselbe Energie.

Warum? Das ist die zentrale Frage! Weil sich denkbare Unterschiede im Laufe der Zeit durch die Wechselwirkung (= Stöße) nivellieren. Schauen wir das System "Gas im geschlossenen Hörsaal" an: Wenn in einer Ecke die Stickstoff- und Sauerstoffmoleküle aus irgendeinem Grund plötzlich viel schneller wären als der Rest, werden sie bei jedem Stoß mit einem langsameren Kollegen im Mittel mehr Energie abgeben als aufnehmen – und zwar so lange, bis alle wieder im Mittel gleich sind. Für die Elektronen gilt das genauso.

Das ist uns aus dem täglichen Leben so wohlvertraut, daß wir die Einstellung des so beschrieben Gleichgewichts gar nicht mehr hinterfragen.

Wir können diesen alltäglichen Sachverhalt, daß sich bei Vorliegen eines Gleichgewichts im Mittel räumlich und zeitlich nichs mehr ändert, auch so ausdrücken:

Im Gleichgewicht ist die Besetzung der verfügbaren Energieniveaus überall und immer dieselbe.

Wenn links unten im Gas im einem Volumenelement von ca. 10 nm³ im Mittel 234 Atome mit ½mv₁² herumflitzen, 86 mit ½m v₂² und v₂ > v₁, während es bei v₃ > v₂ nur noch 17 Teilchen sind, dann wird in einem gleichgroßen Volumenelement irgendwo an der Spitze des Ortsvektors r es im Mittel genauso sein.

Falls wir ein derart definiertes Gleichgewicht haben, ist die innere Energie offenbar gleichverteilt.

Zweite Schlußfolgerung / Definition: Bei Gleichverteilung der Energie (= Gleichgewicht) erhält die im System steckende konstante innere Energie U für klassische Teilchen einen eigenen Namen. Als Maß für die innere Energie benutzen wir das uns bereits bekannte Wort (absolute) "Temperatur" , immer gemessen in K (Kelvin).

Damit haben wir erstmals den Alltagsbegriffbegriff "Temperatur " sauber definiert. Als formale Definition der Temperatur benutzen wir den sogenannten Gleichverteilungssatz. Wir kennnen ihn schon (wenn auch nicht unter diesem Namen), er lautet:

Bei der (absoluten) Temperatur T hat ein klassisches Teilchen
in einem Teilchensysten (Kristall, Gas, ...) im Mittel die innere (thermische) Energie

U_Teilchen= ½fk_BT

(mit f = Zahl der Freiheitsgrade für Energieaufnahme).

Auch die Bedeutung des ominösen "f = Zahl der Freiheitsgrade für Energieaufnahme" haben wir uns schon angeschaut.

Wir halten dazu nochmals fest:

Für einatomige Gase ist f = 3, entsprechend der 3 Möglichkeiten, in x- y- und z-Richtung kinetische Energie zu deponieren.
Für zwei- oder mehratomige Gase ist f > 3, weil Energie noch in diverse Rotations- und Schwingungszustände gesteckt werden kann.
Für Kristallatome ist f = 6 (dreimal kinetische und dreimal potentielle Energie); vgl. das Bild oben.

Das ist aber für ET&IT-Studis nicht so wichtig. Es reicht vollständig und ist erforderlich zu wissen:

Thermische Energie (Größenordnung von U_Teilchen):

U_Teilchen» E_therm = k_BT

E_therm(300 K) » 1/40 eV

Zeit für eine Übung:

Übungsaufgabe
Aufgabe 5.1-1: Mittlere Energien

Die Sache mit den Elektronen = Fermionen

Wie ist das nun bei nicht-klassischen Teilchen wie unseren Elektronen?

Ganz anders!

Das Wort "Temperatur" hat für unsere im Kristall herumsausenden Elektronen eine ganz andere Bedeutung als für unsere "klassischen" Atome. Das kann man ganz leicht einsehen: Kühlen wir unser "Elektronengas" ab, würde die innere Energie bei Gültigkeit des Gleichverteilungssatzes im Extremfall auf (nahezu) null absinken. Das würde aber bedeuten, daß alle Elektronen auf dem niedrigsten Energieniveau (bei E = 0) zu sitzen kämen – und damit alle denselben Zustand besetzten. Da aber der Entartungsgrad des Grundzustands immer sehr viel kleiner ist als die Zahl der Elektronen, geht das nicht!

Herr Pauli hat's "verboten"! Das Pauli-Prinzip ist absolut unverletzlich; es gilt immer. Die Elektronen besetzen deshalb auch die energetisch höher gelegenen Niveaus.

Das hat eine enorm wichtige Konsequenz: Die gesamte Energie der Elektronen geht deshalb nicht mit der Temperatur gegen null!

Aber was bedeutet dann "Temperatur"?

Statt eine pauschale Temperatur als makroskopischer Kenngröße für das gesamte System anzugeben, ist es notwendig, etwas differenzierter vorgehen. Wir brauchen zur pauschalen Beschreibung eines "Elektronengases" im Kristall zwei Größen:

Eine Zahl, nämlich den Wert der Energie (in eV), bei der auch das letzte Elektron für minimale Gesamtenergie (bei T = 0 K) untergebracht werden kann. Diese wohldefinierte Energie nennen wir Fermienergie ; sie ist eine der wichtigsten Kenngrößen für Halbleiter.
Eine Funktion für die Zahl z(E) (oder Dichte D(E), d.h. z per cm³), die uns sagt, wieviele Zustände es bei E gibt, d.h. wieviele Elektronen bei der Energie E untergebracht werden können. Das ist sowas wie der Entartungsgrad.

Diese beiden Systemgrößen werden in so gut wie jeder Gleichung für Halbleiterbauelemente wie Transistoren auftauchen, man kann sich gar nicht früh genug damit vertraut machen.

Der 1. Hauptsatz der Thermodynamik

Der berühmte 1. Haupsatz der Thermodynamik ist nichts anderes als der uns wohlbekannte Energieerhaltungssatz . In den obigen Betrachtungen steckt er schon drin ("Die Summe der in den individuellen Bewegungen der Atome steckenden inneren Energie ist konstant").

Die "Berühmtheit" kommt schlicht vom historischen Ballast: Solange völlig unklar war, was "Wärme " eigentlich ist, hatte die Thermodymanik eine Sonderstellung und ein Problem. Mit "Wärmekraftmaschinen" wie den frühen Dampfmaschinen konnte man einiges machen, es paßte aber nicht so recht zur damals schon bekannten Newtonschen Mechanik. Die entscheidenden Erkenntnisse waren, daß (i) Wärme Q, gemessen in Kalorien oder sonstwas, schlicht eine Energieform ist, und daß sie aber (ii) keine Zustandsgröße ist (wie die Temperatur oder die innere Energie), sondern eine Prozeßgröße; dieser Link gibt ein paar Hinweise auf die zugehörige Geschichte.

Man kann ihn auch so formulieren

Es gibt kein Perpetuum Mobile!

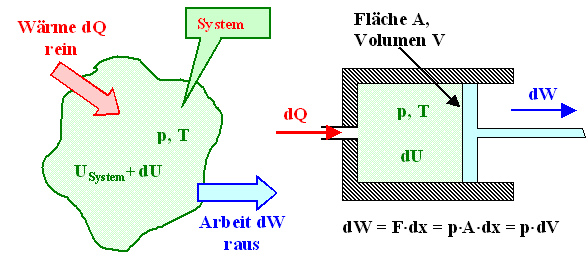
Mit DU = Änderung der inneren Energie U des betrachteten Systems bei dem betrachteten Prozeß, Q = zugeführte Wärmeenergie, W = nach außen geleistete mechanische Arbeit, läßt sich der 1. Haupsatz wie folgt formulieren:

DU = Q – W

Das ist der Energieerhaltungssatz unter Einschluß der Wärmeenergie "Q". In Worten besagt obige Gleichung:

Die (resultierende) Änderung DU der im System vorhandenen inneren Energie U ist gleich der zugeführten Wärmeenergie Q minus der nach außen geleisteten Arbeit W.

Die nach außen geleistete Arbeit resultiert in der Regel aus einer Volumenänderung – der paradigmatische Kolben bewegt sich in einem Zylinder, z.B. in der Wärmekraftmaschine Benzin- oder Dieselmotor.

Statt dem "Änderungs D " wird oft das "Differenzierungs d" des totalen Differentials geschrieben, das ist aber nicht so ganz richtig. Warum das so ist, kann man sich aus den Links zusammenreimen. Für unsere Zwecke ist der feine Unterschied aber bedeutungslos.

So genau wollen wir das aber hier gar nicht wissen. Wer nur mal sehen will, wie's weitergeht und wie man aus der obigen simplen Gleichung noch allerlei herausholen kann, der betätige den Link.

Hier listen wir nur mal kurz die Fragen auf, die uns der 1. Hauptsatz (auch bei intensiver Pflege) nicht beantwortet:

Wie ist das mit der Verteilung der im System steckenden inneren Energie U auf die Elektronen / Fermionen?
Allgemeiner: Nach welchem Prinzip ergibt sich der stabile Zustand des Systems (= Gleichgewicht); der 1. Haupsatz alleine ist ja mit vielen denkbaren Mikrozuständen verträglich.

In Worten: Der 1. Haupsatz verlangt nur, daß Energie nicht aus Nichts entsteht oder einfach verschwindet. Es ist ihm aber egal, ob die innere Energie eines Gases nur in 10 Atomen steckt oder gleichverteilt in allen. Es ist ihm auch egal, ob die Atome im "Gleichtakt" fliegen oder vibrieren, oder statistisch ungeordnet. Der schon eingeführte Gleichverteilungssatz folgt also nicht unmittelbar aus dem 1. Hauptsatz.

Wir brauchen ein 2. Prinzip, das klärt, welche der vielen mit dem 1. Hauptsatz verträglichen Möglichkeiten wirklich vorliegt.

Dieses Prinzip ist der 2. Haupsatz der Thermodynamik, der im nächsten Unterkapitel behandelt wird. Er dreht sich um den Begriff der Unordnung in Systemen, oder wie wir das zukünftig nennen wollen, ihrer Entropie .

Hier die schnellen Fragen:

Fragebogen
Schnelle Fragen zu 5.1.1