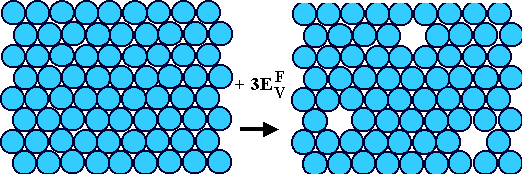5.1.2 Der 2. Hauptsatz und die Entropie

Unordnung und Entropie

	Um ein Gefühl für die Bedeutung von Unordnung oder Entropie zu entwickeln, betrachten wir mal zwei einfache Beispiele: Einen einfachen Kristall aus zwei Atomsorten A und B, bei dem die Bindungsenergie zwischen allen Beteiligten immer gleich groß ist, d.h. U A–A = UB–B = UA–B . Wer das gekünstelt findet, nimmt zwei verschiedene Isotope derselben Atomsorte - es kommt nur darauf an, dass wir A und B unterscheiden können. Einen perfekten Kristall aus einer Atomsorte mit und ohne ein paar Leerstellen
		Wie das aussieht, ist hier gezeigt:
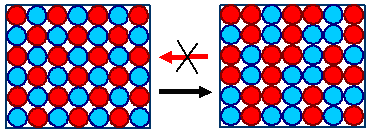
	Im ersten Fall könnten die A- und B-Atome vollständig regelmäßig (d.h. in perfekter Ordnung ) die Gitterplätze besetzen (wie links gezeichnet), sie könnten das aber auch "rein statistisch" in perfekter Unordnung tun, wie im rechten Bild (für jeden Platz eine Münze werfen; Kopf = rot, ...).
		Was werden sie denn tun? Der 1. Hauptsatz sagt dazu gar nichts. Die innere Energie ist für jede der beiden Anordnungen dieselbe, auch dann noch, wenn man die Schwingungen um die Gleichgewichtslage mitnimmt.
		Die Erfahrung sagt aber ganz klar, dass es ziemlich unwahrscheinlich ist, perfekte Ordnung zu finden. Spätestens wenn wir noch zulassen, dass die Atome sich (per Diffusion) etwas bewegen können, wird Ordnung, falls sie jemals existierte, nicht lange aufrecht erhalten werden können. Die Grundaussage ist also:
		Bei gleicher innerer Energie sind unordentliche Anordnungen der Teilchen des Systems viel wahrscheinlicher als ordentliche Anordnungen.
		Das ist eigentlich ziemlich trivial: Es gibt einfach unglaublich viele Möglichkeiten, einen unordentlichen Zustand zu erwürfeln, und nur eine sehr, sehr unwahrscheinliche Möglichkeit, die perfekte Ordnung zu erwürfeln. Anders ausgedrückt: Sehr viele Wege führen vom ordentlichen Ausgangszustand zur Unordnung, aber nur einer von sehr vielen Wegen führt vom unordentlichen Zustand zur Ordnung.
	Das gilt in noch viel stärkerem Maße für das erste System (ein Gas), das wir im vorhergehenden Unterkapitel angeschaut haben.
		Stellen wir uns zwei Teilchensorten vor (O2 und N2, blau oder gelb, ...), dann könnten wir die Teilchen halbwegs ordentlich im gegebenen Volumen unterbringen, indem wir die blauen eher links und die gelben eher rechts halten. Nicht besonders ordentlich, aber definitiv ordentlicher als eine rein statistisch durchgemischte Anordnung. An den Geschwindigkeiten ändern wir nichts, also ist die innere Energie immer dieselbe.
		Das Bild zeigt, wie das aussieht – einfach nur absurd. Gibt's nicht; sowas macht Mutter Natur niemals. Zumindest ist es sehr unwahrscheinlich, dass in einem gegebenen Volumen (der Hörsaal) sich alle Stickstoffmoleküle hinten und die Sauerstoffmoleküle alle vorne befinden – und sei es auch nur ganz kurzzeitig! Direkt verboten ist das aber auch nicht.
	Wie wahrscheinlich es wäre, ist leicht auszurechnen:
		Teile das verfügbare Volumen in soviel Volumenelemente wie Moleküle vorhanden sind (= N). Werfe für jedes Volumenelement eine Münze: Kopf: O2 geht ins Volumenelement, Zahl: N2 geht ins Volumenelement.
		Wie groß ist die Wahrscheinlichkeit w(N), dass für die Volumenelemente 1, 2, ..., N/2 (mit N so um die 1024) immer nur Zahl geworfen wird? Nun ja, w(N) ist nicht exakt null, aber schon sehr, sehr klein.
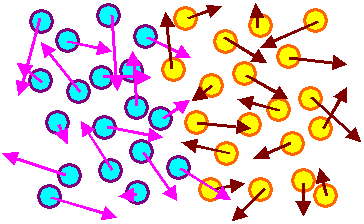		Ordentliche O2/N2-Molekülverteilung im Hörsaal; eher unwahrscheinlich (dem 2. Hauptsatz sei Dank)
	Wiederum ist offenbar von allen möglichen Anordnungen mit gleicher innerer Energie die mit der größten Unordnung am wahrscheinlichsten. Schlicht und ergreifend deswegen, weil es nur wenige Möglichkeiten gibt, eine ordentliche Verteilung zu "würfeln", aber sehr viele Möglichkeiten für Unordnung.

	Jetzt schauen wir uns das Bild des Kristall mit Leerstellen an. Relativ zum perfekten Kristall links hat derselbe Kristall mit drei Leerstellen eine höhere innere Energie – wir mussten dreimal die Bildungsenergie einer Leerstelle, also 3EVF, hineinstecken, um die Leerstellen zu erhalten.
		Trotzdem werden wir bei höheren Temperaturen den Kristall voller Leerstellen finden – mit einer Konzentration cV = exp (–EVF/kBT) wie bereits gehabt. Mit diesen Leerstellen ist der Kristall definitiv unordentlicher als mit keinen, und sein Grad an Unordnung nimmt mit steigender Leerstellenkonzentration, also mit steigender Temperatur, zu. Leerstellen sind in dieser Betrachtung "unaufgeräumte" Atome.
		Das ist ein deutlicher Hinweis darauf, dass das System "Kristall" nicht unbedingt nur den Zustand mit der kleinstmöglichen Energie und gleichzeitig größtmöglichen Unordnung anstrebt, sondern bereit ist, für mehr Unordnung mit etwas mehr Energie "zu bezahlen". Je höher die Temperaturen, umso mehr "wert" scheint Unordnung zu sein.
		Wenn wir ein bißchen nachdenken, ist das ein generelles Prinzip: mit zunehmender Temperatur steigt die Unordnung von so ziemlich allem (und die Energie). Es scheint auf die richtige Balance anzukommen.
	Bei einer bestimmten Temperatur, die wir Schmelzpunkt Tm nennen, wird das Ganze sogar "makroskopisch" sichtbar:
		Eine Schmelze ist definitiv eine sehr viel unordentlichere Anordnung von Atomen als ein Kristall mit Defekten. Es braucht aber nicht ganz wenig Energie (die "Schmelzwärme"), um bei Tm aus einer festen Phase eine flüssige zu machen – trotzdem schmelzen die Kristalle!
		Offenbar ist das System "großer Haufen Atome" aber bereit, am Schmelzpunkt diesen "Energiepreis" zu bezahlen. Der große Gewinn an Unordnung bei der Schmelzpunktstemperatur wiegt die Energieinvestition offenbar auf - es lohnt sich, bei Tm diese Investition zu machen. Bei kleineren Temperaturen lohnt es sich nicht, deshalb bleibt der Kristall fest.
		Auch wenn das ein bißchen merkwürdig erscheint: Der Zugewinn an Unordnung, oder wie wir das jetzt nennen wollen, an Entropie, ist der einzige Grund dafür, dass Materialien schmelzen.
	Das Prinzip, nach dem ein System "entscheidet", was es tut, ist also: Finde die optimale Balance zwischen minimaler Energie und maximaler Unordung.
		Das zwar ein interessantes aber nutzloses Prinzip, solange wir es nur in Prosa aufstellen. Als Ingenieure wollen wir Dinge berechnen, und dazu benötigen wir wohl oder übel ein Maß für die Unordnung, so daß wir sie mit einer Zahl versehen können. Wir wollen nicht mehr nur sagen "mein Zimmer ist heute viel ordentlicher als gestern" sondern "mein Zimmer hat heute eine Unordnung von 17 verglichen mit den gestrigen 132". Dazu definieren wir die Entropie als "quantitatives Unordnungsmaß".

	Quantitative Definition der Entropie
	Für eine "gemessene" Unordnung benutzen wir nur noch den Begriff Entropie S, mit der Maßeinheit eV/K (K =Kelvin). Warum das eine sinnvolle Maßeinheit ist, wird sich in Kürze zeigen.
		Wie mißt man den Grad an Ordnung oder Unordnung in einem System? Eine schwere Frage für die immer noch überwiegend männlichen Ingenieure, obwohl ihre Mütter mit hoher Wahrscheinlicheit sehr oft versucht haben, ihnen beizubringen, was Ordnung ist. Eigentlich ist es ganz einfach:
		Ordnung heißt: Jedes Ding ist an seinem Platz. Es gibt nur einen Platz für jedes Ding.
		Man denke an das perfekt aufgeräumte Zimmer, und man erkennt, daß einerseits die Definition ganz sinnvoll ist, andererseits perfekte Ordnung auch hier einen eher unwahrscheinlichen Zustand darstellt.
		Im Umkehrschluß bedeutet dies: Es gibt nur eine einzige Möglichkeit, perfekte Ordnung einzustellen! Im aufgeräumten Zimmer ist jedes Ding an seinem Platz, im perfekten Kristall ist jedes Atom an seinem Platz.
	Es gibt aber viele Möglichkeiten, ein unordentliches Zimmer, einen unordentlichen Schreibtisch oder einen unordentlichen Kristall zu produzieren. Es gibt sehr viele Möglichkeiten, 10 dreckige Socken auf die vorhandenen Plätze in Zimmer zu verstreuen - einer auf dem Schreibtisch, einer unter dem Bett, einer hinter der Tür, usw. - aber nur einen einzigen richtigen Platz (Hinweis für die Männer: den Wäschekorb).
		Es gibt also viele grundsätzlich äquivalente Möglichkeiten, Unordnung in einem Zimmer (oder in einem Kristall) zu erzeugen. Diesen Ansatz über die Möglichkeiten kann man verallgemeinern und quantifizieren.

	Quantifizieren wir mal das Sockenbeispiel: Wir haben n Socken und N Plätze, auf die wir Socken verteilen können. Damit kann man anfangen zu rechnen.
		Makroskopisch sind n und N die beiden einzigen Größen, die das Zimmer-Socken-System (ZS-System) charakterisieren. Jedes mögliche Wertepaar von n und N definiert damit einen spezifischen makroskopischen Unordnungszustand, kurz einen Makrozustand (n, N) des ZS-Systems.
		Aber zu jedem möglichen Makrozustand gibt es viele Mikrozustände oder Realisierungsmöglichkeiten, zum Beispiel:
		Zu dem ZS-Makrozustand (5,23) gehört folgende Mikrozustände Socken Nr. 1 auf Platz 1, Socken Nr. 2 auf Platz 2, ... Socken Nr. 3 auf Platz 1, Socken Nr. 5 auf Platz 2, ... usw. – aber nicht ad infinitum! Die Liste hört irgendwann auf, sie läuft von 1., 2., 3., bis zu einer Zahl p, die wir mit hinreichend viel Kombinatorik-Kenntnissen ausrechnen können.
	Nehmen wir jetzt Leerstellen statt Socken und einen Kristall statt einem Zimmer, dann ist der Makrozustand durch die Zahl n der Leerstellen und die Zahl N der verfügbaren Plätze im Kristall gegeben.
		Die makroskopischen Eigenschaften des Kristalls hängen nur von diesem Makrozustand ab, d.h. von der Konzentration cV = n/N der Leerstellen. Welcher der vielen möglichen Mikrozustände zu einer gegebenen Konzentration realisiert ist, spielt dabei keine Rolle.
	Schauen wir uns mal qualitativ an, was für Möglichkeiten wir haben, um Leerstellen im Kristall anzuordnen:
		Zum Makrozustand i = 0: "Alle Atome auf ihren Plätzen"; d.h es gibt keine Leerstellen, oder (n, N) = (0, N) gibt es nur einen Mikrozustand, eben alle Atome auf ihren Plätzen – perfekte Ordnung!
		Zum Makrozustand i = 1: " Eine Leerstelle irgendwo"; oder (n, N) = (1, N) gibt es genau p1 = N Mikrozustände, die Leerstelle kann auf jedem der N Plätze sitzen.
		Zum Makrozustand i = 2: "Zwei Leerstellen irgendwo"; oder (n, N) = (2, N) gibt es auf jeden Fall mehr als N Möglichkeiten, d. h. p2 > p1; wieviel genau werden wir noch ausrechnen.
		Und so weiter. Für drei Leerstellen gibt es mehr Mikrozustände als für zwei – die Zahl der Mikrozustände pi steigt jedenfalls mit n = i. Gleichzeitig wird der Kristall immer unordentlicher, so wie ein Zimmer mit 30 verstreuten Socken noch unordentlicher ist als eines mit nur 5.
	Wir erkennen:
		Die Zahl pi der möglichen Mikrozustände zum Makrozustand Nr. i ist ein quantitatives Maß für den Grad der Unordnung dieses Zustands.
	Damit können wir jetzt die Entropie quantitativ definieren: Das ist die berühmte Formel von Boltzmann, die wir hier in leicht vereinfachter Form benutzen:
		Si  = kB · ln  pi
		Die Größe kB ist die mit Recht so genannte Boltzmannkonstante. Boltzmannkonstante und Entropieformel haben ungefähr den gleichen "Rang" wie Lichtgeschwindigkeit c und E = mc2 oder Plancksche Konstante h und E = hn.
	Die schlechte Nachricht ist aber: Die obige Entropieformel ist schwierig in der Anwendung. Man muss tief in die Kombinatorik einsteigen und sich vorher noch klar darüber werden, was genau man "kombiniert". Wie groß ist die Entropie von n Photonen in einem Spiegelkasten? Sehr schwer zu beantworten – Planck hat beim jahrelangen Nachdenken über diese Frage seine Strahlungsformel gefunden!
		Die gute Nachricht ist: Meistens ist es nicht erforderlich, die Formel so, wie sie dasteht, zu verwenden. Herr Boltzmann und Kollegen haben eine universelle "Abkürzung" gefunden, die das Ganze ziemlich einfach macht. Bevor wir das aber im nächsten Kapitel kennenlernen, gehen wir zur Übung erst einmal "in die Vollen" und x-en das Lerstellenbeispiel von oben durch.

	Beispiel: Die Entropie von Leerstellen im Kristall
	Wir betrachten n Leerstellen in einem Kristall bestehend aus N Atomen und berechnen jetzt die Entropie S(n).
		Mit der Entropieformel Si = k B · ln pi von Boltzmann ist das leicht (haha) möglich.
	Die Frage ist zunächst, wieviel Mikrozustände pi es zum Makrozustand i = "n Leerstellen verteilt auf N Plätze" gibt. Es kann natürlich immer nur eine Leerstelle auf einem Platz sitzen. Die Zahl der Mikrozustände ergibt dann das pi für die Formel.
		Das ist eine Standardaufgabe aus der elementaren Kombinatorik. Die Formel dazu ist leicht herzuleiten; wir betrachten dazu eine Tabelle der Möglichkeiten, beginnend bei n=0.
		n (= i) pi = Kommentar 0 1 Es gibt genau eine Möglichkeit, keine Leerstelle zu haben: Alle Atome auf ihren Plätzen. 1 N Es gibt N Plätze für die 1. Leerstelle und damit N Mikrozustände. 2 N · (N – 1) 2 Es gibt N Plätze für die 1. Leerstelle und noch N – 1 Plätze für die 2. Leerstelle. Vertauschen bringt jedoch nichts Neues – die Anordnungen sind ununterscheidbar. Wir müssen also noch durch 2 dividieren. 3 N · (N – 1) · (N – 2) 2 · 3 Vertauschen aller 3 Leerstellen bringt nichts neues, da die möglichen Anordnungen alle ununterscheidbar sind, wir müssen deshalb durch 6 = 2 · 3 dividieren. ... ... usw. n N· (N– 1) · (N – 2) · .... · (N – (n – 1)) 1 · 2 · 3 · ... · n Wir haben ein offenkundiges Bildungsgesetz. Der Nenner ist per definitionem n! (gesprochen "enn Fakultät"). n N · (N – 1) · (N – 2) · .... · (N – (n – 1)) n! · (N – n)! (N – n)! Kleiner Trick: Wir erweitern mit (N – n)! und erhalten: n N! n! · (N– n)!  =  æ è N n ö ø Das ist eine so häufige Formel, dass sie einen eigenen Namen und Symbol hat: æ è N n ö ø  =  Binomialkoeffizient

	Die Entropieformel lautet damit
		Sn = kB· ln æ è N! n! · (N– n)! ö ø  =  kB · æ è ln N! – ln n! – ln (N – n )! ö ø
		Sieht geil aus, aber was nützt's? Gemach, wir werden die Nützlichkeit dieser Formel im nächsten Kapitel schon noch sehen. Hier geht es nur darum zu zeigen, dass es "geht" - wenn auch mit Mühe.

	Der 2. Hauptsatz der Thermodynamik
	Wir krönen diese Kapitel mit einer noch einfachen Variante des 2. Haupsatzes der Thermodynamik :
		Im thermodynamischen Gleichgewicht hat ein System eine möglichst große Entropie und Die Entropie eines abgeschlossenen Systems wird nie von alleine kleiner.
	Der erste Satz ist klar, der zweite Satz hat es in sich und muß erklärt werden.
		Der 2. Hauptsatz definiert irreversible Prozesse: Denn ein Prozeß, bei dem die Entropie zunimmt, kann offenbar geschehen, der Rückwärtsprozeß jedoch nicht. Die Konsequenz daraus ist:
		Der 2. Hauptsatz definiert eine Richtung der Zeitachse: Auf der Zeitachse kann man sich nur in Richtung höherer Entropie bewegen. (Der 2. Hauptsatz ist im übrigen das einzige Naturgesetz oder Axiom, das eine Zeitrichtung kennt. Wenn man bedenkt, wie fundamental es für uns ist, daß die Zeit immer nur in eine Richtung fließt, ist das schon sehr erstaunlich!)
		Der 2. Hauptsatz definiert den Wärmetod des Universums: Irgendwann wird universelles Gleichgewicht (im wahrsten Sinne des Wortes) und damit maximale Unordnung erreicht sein. Nichts wird sich mehr ändern - das Universum hat den Wärmetod erlitten.
	Man sieht: Der 2. Haupsatz hat erheblichen Tiefgang. Wir können das hier aber nur ganz oberflächlich ausloten. Zum Schluss noch eine weitere Formulierung des 2. Haupsatzes, die man oft antrifft:
		Es gibt kein Perpetuum Mobile 2. Art!
	Was ist ein Perpetuum Mobile 2. Art? Das beim 1. Hauptsatz erwähnte war dann wohl ein Perpetuum Mobile der 1. Art?
		So ist es. Ein Perpetuum Mobile 1. Art generiert Arbeit = Energie aus dem Nichts - das gibt's nicht. (Zumindest ist bislang das Gegenteil nicht bewiesen worden, allem Gerede über esoterische "freie Energie" zum Trotz.)
		Ein Perpetuum Mobile 2. Art würde Arbeit generieren, indem es aus einem Wärmereservoir (z. B. die Weltmeere) Wärme = Energie entnimmt und vollständig in mechanische Arbeit umwandelt; das Meer muss sich dabei irgendwie abkühlen. Dabei bleibt zwar die Gesamtenergie erhalten, aber die Entropie sinkt.
		Auch das gibt's nicht. Leider.
	Man kann das auch so formulieren: 1. Haupsatz: You can't win. 2. Haupsatz: You can't even break even.
		Fragebogen Schnelle Fragen zu 5.1.2

© H. Föll (MaWi für ET&IT - Script)