|
Ein thermodynamisches System besteht aus einer großen Zahl von Teilchen,
die miteinander in Wechselbeziehung in Form von Energieaustausch stehen. |
|
|
|
 |
Es gibt eine definierte Zahl an Möglichkeiten (= Freiheitgrade
f) in den Teilchen, Energie zu "haben" (Bewegung, Rotation, Potential, ...) |
|
|
 |
Im Gleichgewicht gilt dann für klassische Teilchen
der Gleichverteilungssatz (= Definition der Temperatur). |
|
|
| |
|
|
|
| |
|
| |
| |
 |
Für T
® 0 K folgt Utherm = 0 eV; d. h. alle Teilchen im selbem Zustand
Þ | |
| Der Gleichverteilungssatz gilt nicht
für Fermionen! |
|
|
 |
Trotzdem ist im Gleichgéwicht die Besetzung der vorhandenen Energie-Zustände immer
dieselbe. | |
|
| |
| |
 |
Es gilt immer der Energieerhaltungssatz =
1. Haupsatz der Themodynamik. |
|
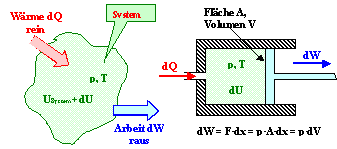 |
| DU = DQ
– DW |
|
|
 |
Der Gleichverteilungssatz folgt nicht aus dem 1.
Haupsatz. | |
|
 |
Der 1. Hauptsatz regelt nicht, wasmikroskopisch vorliegt, d.h. welche
innere Energien
U die Teilchen im Mittel haben = welche Energieniveaus durch wieviel Teilchen besetzt sind. |
|
|
 |
Es wird ein 2. Prinzip benötigt. |
|
|
| |
| |
 |
Die Entropie
S ist ein quantitatives Maß für Unordnung. |
|
|
|
 |
Die Zahl pi beschreibt die Zahl der mikroskopisch möglichen
Anodnungen der Teilchen zum selben Makrozustand i. |
|
|
|
| 2. Hauptsatz: |
Im thermodynamischen Gleichgewicht hat ein System eine möglichst große Entropie
und
Die Entropie eines abgeschlossenen Systems wird nie von alleine kleiner |
| |
| Entropie von n Leerstellen und N – n Atomen |
| Sn | = |
kB · ln | æ
è |
| N!
n! · (N – n)! | |
ö
ø | | |
| | |
| | |
= | kB · |
æ
è |
ln N! – ln n! – ln (N – n)! |
ö
ø |
|
|
| |
|
|
| |
|
|
 |
Beispiel: Leerstellen machen Unordnung. Die zugehörige Entropie kann man (mühsam)
ausrechnen. | |
|
| |
| |
© H. Föll (MaWi für ET&IT - Script)