|
Im vorhergehenden Kapitel haben wir uns klar gemacht, wie die E(k)
- Kurve eines realen Kristalls prinzipiell aussehen muß. |
|
 |
Wir nehmen nun diese Kurve und fragen uns, wie sie wirklich
aussieht. Dazu müssen einige prinzipielle Erkenntnisse einfließen, die von der Festkörperphysik mit harten
Rechnungen erarbeitet wurden. |
|
 |
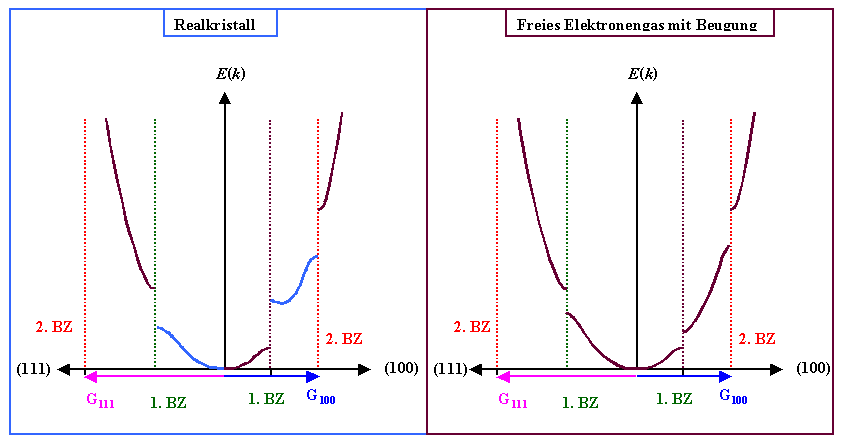
Um das zu verstehen, stellen wir einfach die alte
"Prinzip"kurve und die reale Kurve eines realen Kristalls einander gegenüber: |
| |
|
 |
Im Grunde brauchen wir nur zwei, "irgendwie" auch ohne lange Rechnung
verständliche Verallgemeinerungen: |
|
1. Die Größe der Aufspaltung,
d.h. die Breite der Energielücke, ist kristall- und richtungsspezifisch. Das ist
im linken Ast für die Kurve in der 1. BZ angedeutet. |
|
 |
Das heißt, z.B. daß die Energielücke in der {100}-Richtung des Si
verschieden sein wird von der im Ge, oder GaAs, oder ..., (immer im reziproken Gitter natürlich).
|
|
 |
Es heißt auch, daß die Energielücke in der {100}-Richtung des Si
verschieden sein wird von der Energielücke in der {111}-Richtung des Si, oder der {110}-Richtung,
oder der {hkl}-Richtung. Allerdings sind natürlich Kristallsymmetrien gewahrt, d.h. die geschweiften Klammern sind absichtlich gesetzt. |
 |
2. Der genaue Verlauf der E(k) Kurve kann sich
kräftig von der einfachen Parabel des freien Elektronengases unterscheiden. Das ist im rechten Ast für die Kurve
in der 2. BZ angedeutet. |
|
 |
Insbesondere muß das Minimum oder
Maximum des Energiewertes für irgendeinen Zweig, so wie im rechten
Ast gezeigt, nicht unbedingt auf dem Rand einer BZ
liegen. Das wird weitreichende Konsequenzen haben. |
 |
Unterstellen wir einfach, daß die richtigen Kurven für einen gegebenen
Kristall in allen Details bekannt sind (falls nicht gerechnet, dann wenigsten gemessen), dann haben wir alles was wir brauchen.
Das Problem ist nur: Viele Kurven in all diese Richtungen - es wird unübersichtlich. |
|
 |
Wir gehen deshalb über zu einer stark vereinfachten
Darstellung der Elektronen in Kristallen: Wir betrachten nur noch, welche Energiewerte erlaubt, und welche verboten sind
- für beliebige Richtungen. Das Ergebnis ist dann ein Banddiagramm. |
|
 |
Wie man vorgeht ist im nächsten Bild schematisch gezeigt; wir bedienen uns der Kurve
aus dem obigen Bild. |
|
|
|
 |
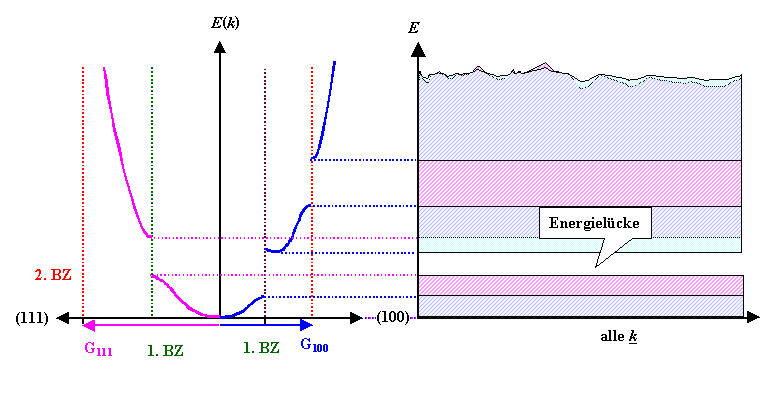
Wir projezieren einfach alle erlaubten Energiewerte
für alle Richtungen auf ein
E(k) Diagramm, wobei wir aber den jeweiligen k-Wert gar nicht mehr betrachten.
|
|
 |
Gezeigt ist die Projektion von zwei Ästen der Dispersionskurve,
die zwei Teilbänder ergeben. Wir können die Vorgehensweise natürlich
"leicht" auf alle Äste ausdehnen, die dadurch erhaltenen "Bänder" aller möglichen Energiewerte geben
dem Diagramm den Namen: Es heißt Banddiagramm. |
|
 |
Die Energielücke ist prominent zu sehen, wir nennen sie ab jetzt auch Bandlücke,
oder in Denglisch "Bandgap". |
|
 |
Wir haben zwar nach wir vor zu jeder beliebigen herausgegriffen Energie (mehrere) bestimmte
k-Werte, aber die interessieren uns nicht mehr. |
|
 |
Falls wir das Banddiagramm als stark vereinfachte Darstellung der Gesamtheit der E(k)
Kurven betrachten, steht an der x-Achse natürlich k. Wir können aber die Achsenbezeichnung
im Moment auch weglassen, da sie keinerlei Information enthält. |
|
 |
Wir können noch einen Schritt weitergehen und z.B
auch "x" oder "z" oder <110> an die Abszisse schreiben , d.h.
eine Darstellung der erlaubten Energien im Ortsraum wählen - das Banddiagramm sieht
genau so aus. |
 |
Das sieht wirklich nach einer massiven Vereinfachung aus. Aber das werden wir
auch brauchen, denn aus dem hier noch einfachen Banddiagramm wird schnell genug wieder ein kompliziertes Gebilde werden. |
| |
|
|
Zahl der Zustände in einem Band |
| | |
 |
Wieviele Zustände NB gibt es in einem Band? Dazu
muß man nur die Zustandsdichte über
die Energie von der Bandunterkante bis zur Bandoberkante integrieren - leider kennen wir die Zustandsdichte nicht mehr. |
|
 |
Die Frage ist trotzdem ganz leicht zu beantworten - wenn wir ein bißchen
nachdenken. Man kann sogar eine Antwort aus zwei grundverschiedenen Betrachtungsweisen finden, die wir beide kurz anschauen: |
|
 |
1. Abzählen der möglichen Wellenvektoren in einer BZ, und
|
|
 |
2. Betrachtung der Aufspaltung der Energieniveaus
der Einzelatome bei der Bildung eines Kristalls. |
 |
Im ersten Fall betrachten wir nochmals die Dispersionskurve wie gehabt; schauen
aber etwas genauer auf die k-Achse |
|
|
|
|
|  |
Dort finden wir diskrete Werte für die erlaubten k-Vektoren.
Sie haben auf den k-Achsen, die der <100> Richtung in reziproken Gitter entsprechen, immer den
Abstand
|
| |
| |
| |
|
|
| |
|
|
|
 |
- daran hat sich nichts geändert. |
| |
|
|
 |
Jedes Band entsteht durch die Überlagerung diverser Teilbänder, die
jedoch alle aus derselben Brillouin Zone stammen. Die Breite 2kBZ der Brillouin Zone in Richtung
der <100> Achsen des reziproken Gitters ist aber immer die halbe Länge des reziproken Gittervektors {100}
mal 2 d.h |
| |
|
|
 |
a ist die Gitterkonstante des Raumgitters. Damit passen |
| |
| NB = | 2p
a | : | 2p
L |
= | L
a | = Zahl der EZ |
|
|
|
 |
Zustände in ein Band. Das ist ein einfaches Ergebnis. Wir
haben genau so viel Zustände in jedem Band, wie wir Elementarzellen im Gitter haben.
|
 |
Schauen wir uns das noch in der 2. Betrachtung an |
| |
| |
|
 |
Wir formen einen Na
Kristall, indem wir gedanklich die Potentialtöpfe der Na Atom überlagern.
Das Bild dazu kennnen wir schon und zeigen es nicht nochmal. |
 |
Hier betrachten wir diesen Vorgang etwas quantitativer, indem wir die Größe der
Aufspaltung, d. h. die Differenz zwischen höchster und niedrigster Energie in dem entstehenden Band, über den Abstand der Atome auftragen. |
 |
Aus jedem der bei großem Abstand diskreten Niveaus wird ein Band; die einzelnen Teilbänder
mögen sich bei einem bestimmten Abstand überlappen oder auch nicht. |
 |
Im gezeigten Beispiel Na ist das letzte besetzte Niveau das 3s1
Niveau; wir erwarten den Gleichgewichtsabstand r0 (= Gitterparameter) im Minimum des 3s
Bandes (Warum wohl?). |
| |
|
 |
Die Bandstruktur ergibt sich wie gezeichnet, indem man die jeweiligen Energiewerte
der "Bänder" bei r0 in ein Banddiagramm einzeichnet. |
|
 |
Der Name "Bänder" ist nicht
zufällig derselbe wie beim freien Elektronengas + Beugung - es sind dieselben Bänder,
über die wir hier reden. |
|
 |
Nur können wir hier die Enstehung aus diskreten Energieniveaus der Atome
nachvollziehen und damit auch sofort sagen, wieviele Zustände in einem Band vorliegen: NB =
Zahl der Atome mal Zahl der Zustände in den diskreten Niveaus, aus denen sich das Band zusammensetzt. |
|
 |
Wie so ein Diagramm für Si
aussieht, kann man im Link anschauen. |
 |
Das ist natürlich nicht dasselbe, wie die Zahl der Zustände im ersten
Ansatz. Das kann es aber auch nicht sein, denn im ersten Fall hatten wir ein "leeres Gitter" im zweiten Fall einen
realen Kristall. |
|
 |
Jedenfalls aber halten wir fest: Die Gesamtzahl der Zustände in einem Band
ist eine feste Größe, die unmittelbar aus Gitter, Basis und Bindungsverhältnissen folgt. Sie liegt in der
Größenordnung der Zahl der beteiligten Atome. |
|
| |
 |
Zu Beginn dieses Kapitels haben wir uns gefragt, was bei "Einschalten"
eines periodischen Potentials aus der Zustandsdichte des freien Elektronengases wird und vermutet,
daß es an den Rändern der BZ Änderungen geben muß. |
|
 |
Das können wir ein bißchen vertiefen, wenn wir uns das Banddiagramm
anschauen, wobei wir zunächst mal nur das Banddiagramm eines einzigen "Zweigs" betrachten |
| |
|
 |
Zwei Schlußfolgerungen können gezogen werden - die erste leicht verständlich,
die zweite etwas indirekter |
 |
1. In der Banddlücke gibt es per definitionem
keine Zustände, also muß die Zustandsdichte = 0 sein. |
|
 |
Da wir aber keine Zustände verlieren - wir haben die Zahl der k-Vektoren
schließlich nicht geändert - müssen die Zustände, die vorher in einem Energiebereich waren, der jetzt
der Bandlücke entspricht, irgendwie in die Zustände im Band "gequetscht" werden. |
|
 |
In der Zeichnung ist das angedeutet; es könnten beispielsweise "Spitzen " in
der Nähe der Bandkanten auftreten. Aber genaue Aussagen kann man qualitativ darüber nicht machen |
 |
2. Das freie Elektronengasmodell hat den Nullpunkt der Energie auf einen
willkürlichen Wert gelegt. Im Grunde war das Kriterium, daß für E > 0 die Elektronen frei sein sollen.
|
|
 |
Niemand hält uns nun davon ab, den "Boden" eines Bandes als Nullpunkt der Energie
zu nehmen, d.h. jedes Band als eigenes System in der freien Elektronengasnäherung zu betrachten. Da jedes Minimum (und
Maximum) des Bandes E(k) in erster Näherung durch eine nach oben (bzw. nach unten) geöffnete
Parabel beschrieben werden kann, erhalten wir zumindest in der Nähe der Bandkanten weiterhin eine Dispersionsrelation
wie beim freien Elektronengas, d.h. wir können z.B. auch die Zustandsdichten in der Nähe der Bandkanten weiterhin
sehr gut durch eine Wurzelfunktion D(E) = const. E beschreiben. Nur wird sich im Allgemeinen die Konstante
von der des freien Elektronengases unterscheiden. |
|
 |
Dann hat jedes Band als Zustandsdichte modifizierte Wurzelfunktionen an den Bandkanten und
möglicherweise recht komplizierte Strukturen dazwischen - so wie eingezeichnet. |
 |
Aber es lohnt sich gar nicht, auf die Komplikationen in einem
der vielen Teilbänder einzugehen. |
|
 |
Denn wenn wir jetzt die gesamte Zustandsdichte
in einem Band betrachten, das durch Überlagerung vieler Teilbänder zustande kam, erhalten wir die Überlagerung
vieler mittelkomplizierter Zustandsdichten - das Gesamtergebnis kann beliebig kompliziert sein; das folgende Bild zeigt
die (gemessene) Zustandsdichte von Germanium zusammen mit dem relevanten Teil der Bandstruktur |
| |
|
 |
Damit ist die (theoretische) Lage (fast) hoffnungslos- aber für uns ist das
Leben einfacher geworden: Zustandsdichten muß/kann man messen und hinnehmen! Wir merken uns nur zwei Dinge |
|
 |
Hinter jedem Banddiagramm verbirgt sich immer noch eine i.d.R. komplizierte Zustandsdichte |
|
 |
Die Grundformeln
aus dem 2. Kapitel sind aber nach wie vor gültig. Wir müssen nur (numerisch) die richtige Zustandsdichte einsetzen.
Für analytische Näherungen nutzt man weiterhin die Ergebnisse des Freien Elektronengases mit angepaßten
Konstanten vor der Wurzelfunktion. |
|
 |
In der Nähe einer Bandkante sind alle Zustandsdichten noch "Wurzelfunktionen";
das sieht man in dem Beispiel oben ganz gut. |
|
|
|
© H. Föll (MaWi 2 Skript)