4.2.2 Materialklassen und Banddiagramme

Elektrische Leitfähigkeit in einem Band

	Wir haben gesehen, daß es immer eine definierte Zahl von Zuständen in einem Teilband oder Gesamtband gibt. Diese Zustände wollen wir jetzt mit Elektronen besetzen.
		Damit die Sache einfach bleibt, wählen wir zunächst T = 0 K . Damit steht keine thermische Energie zur Verfügung, die Fermiverteilung ist kastenförmig, und die Elektronen besetzen die vorhandenen Zustände energetisch "von unten kommend" bis alle untergebracht sind.
	Dies läßt für das letzte Band, in dem noch Elektronen untergebracht werden müssen, nur zwei Möglichkeiten zu:
		Alle Zustände im Band sind besetzt, wir haben ein vollbesetztes oder "volles" Band.
		Nicht alle Zustände im Band sind besetzt; wir haben ein teilbesetztes Band.
	Trivial, aber wirkungsvoll. Betrachten wir die folgenden Behauptungen
		1. Elektronen in vollbesetzten Bändern können nicht zur elektrischen Leitfähigkeit beitragen.
		2. In teilbesetzten Bändern können alle Elektronen mit leeren Plätzen in der Nachbarschaft (im k-Raum!) zur elektrischen Leitfähigkeit beitragen.
		3. Falls eine ungerade Zahl von Elektronen auf ein Band zu verteilen sind, ist es immer nur teilbesetzt.
	Hier versteckt sich offenbar eine Klassifizierung aller Materialien in Leiter und Nichtleiter wobei nur einige wenige grundlegende Eigenschaften der Bandstruktur gefragt sind. Machen wir uns zunächst die Punkte 1. - 3. klar:
	Zu 1. Das kennen wir eigentlich schon. Bei der Betrachtung der spezifischen Wärmekapazität des freien Elektronengases haben wir schon gelernt:
		"Wenn ein Elektron Energie aufnehmen will, muß es dazu auf einen anderen Platz bei einer höheren Energie "springen". Falls es aber bei dieser höheren Energie keine freien Plätze gibt, kann der Sprung nicht erfolgen - so einfach ist das!"
		Das gilt natürlich auch, falls die Energieaufnahme durch Beschleunigung in einem elektrischen Feld erfolgen soll, d.h. wenn das Elektron elektrischen Strom leiten soll.
		In einem voll besetzten Band gibt es per definitionem keine leeren Plätze; die Elektronen in diesem Band können also auf nichts (???) reagieren. Die Fragezeichen schränken "das Nichts" etwas ein; wir werden sie später klären.
		Diese Aussagen sind eine direkte Folge der Tatsache, daß Elektronen Fermionen sind, also dem Pauli Prinzip unterliegen. Für Bosonen, also z.B. Photonen, gilt diese Einschränkung (natürlich) nicht. Man stelle sich einmal vor, was passieren würde, wenn man in einen gegebenen Raum nur ein Photon mit einer bestimmten Frequenz hineinpacken dürfte!
	Zu 2. Das versteht sich jetzt von selbst. Wir können das sogar ein bißchen genauer fassen, denn wir wissen schon, daß die Zahl der reaktionsfähigen Elektronen mit der Aufweichungszone der Fermiverteilung zusammenhängen.
	Zu 3. Jeder Zustand eines Atoms kann zwei Elektronen aufnehmen - eines mit Spin "up", und eines mit Spin "down".
		Das gilt auch für die Zustände in einem Band, die man sich ja aus den Atomzuständen durch Aufspaltung entwickeln kann. Damit passen immer 2 mal Zahl der Zustände Elektronen in ein Band - eine immer gerade Anzahl.
		Auch wenn man vom freien Elektronengasmodell her kommt: Auf jedem Zustand, gekennzeichnet durch den Wellenvektor k, haben zwei Elektronen Platz - Spin rauf und Spin runter.
		Damit müßten alle Elemente mit einer ungeradzahligen Anzahl von Elektronen, d.h. mit einer ungeradzahligen Ordnungszahl, im kristallinem Zustand Leiter sein.
		Na ja - ein Blick auf das Periodensystem hilft weiter. Stimmt schon - außer vielleicht für die kristallinen Halogene; aber da werden bei der Kristallisation auch keine "richtigen" Bindungen eingegangen. Aber: Die meisten Elemente mit einer geradzahligen Anzahl von Elektronen sind auch Leiter - also ein besonders tolles Kriterium ist das nicht.
	Immerhin, wir haben erste Zusammenhänge zwischen Bandstruktur und elektronischen Eigenschaften. Klarer wird das ganze erst, wenn wir die Energielücken ins Spiel bringen.
		Das schauen wir uns schnell an:
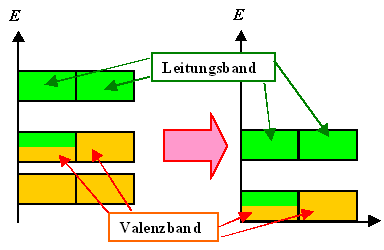
		Links ist eine beliebige Bandstruktur mit mehreren Bändern gezeigt; nochmals unterteilt in die zwei Varianten: Letztes besetztes Band ist teilbesetzt bzw. vollbesetzt. Orange symbolisiert hier besetzte Plätze, im Grünen ist noch was frei.
	Wir treffen jetzt zwei einfache Vereinbarungen:
		1. Das letzte besetzte Band heißt Valenzband. Dabei ist es unerheblich, ob es voll- oder teilbesetzt ist. Das Band direkt darüber heißt Leitungsband. Es ist (zunächst noch) immer leer. Das ist eine etwas vereinfachte Definition; aber für unsere Zwecke ausreichend.
		2. Bänder unterhalb des Valenzbandes zeichnen wir nicht mehr. Die dort sitzenden Elektronen können sowieso nichts tun, sie sind uninteressant und wir lassen sie zukünftig einfach weg.
	Damit erhalten wir die rechts gezeigte Bandstruktur, mit der wir zukünftig arbeiten wollen.

	Isolatoren, Halbleiter und Metalle
	Wir brauchen nur noch eine Zutat, um die in der Überschrift genannten Materialklassen im Bändermodell sortieren zu können: Wir müssen Band-Band-Übergänge betrachten.
		In anderen Worten: Erhält ein Elektron soviel Energie von irgendwoher, daß es die Energielücke überwinden kann, dann kann es unter Umständen vom Valenzband ins Leitungsband springen. Und dort kann es jetzt munter Strom leiten - was es im Valenzband, falls es voll besetzt war, nicht konnte.
		Solche Band-Band-Übergänge, initiiert z.B. durch thermische Energie, ändern somit die elektronischen Eigenschaften des Materials. Sie sind der Dreh- und Angelpunkt der gesamten Halbleitertechnik, und wir werden uns noch heftig damit beschäftigen.
	Hier reicht es völlig, einen simplen Zusammenhang qualitativ zu verstehen (Quantitativ machen wir das in Kürze):
		Ist die Energielücke sehr groß, wird es bei normalen Temperaturen kaum möglich sein, sie durch thermische Anregung zu überwinden, ist sie sehr klein, ist es einfach.
	Damit haben wir zwanglos folgende Klassifikation von Isolatoren, Halbleitern und Leitern anhand von Banddiagrammen:
	Isolatoren sind alle Materialien, die ein vollbesetztes Valenzband und eine große Bandlücke haben. Die angegebenen Zahlen sind natürlich nur Richtwerte, keine scharfen Definitionen. Selbst bei hohen Temperaturen werden es die Elektronen nicht schaffen ins Leitungsband zu wechseln; Stromfluß kann nicht stattfinden.
		Der spezifische Widerstand liegt bei (1010 - 10 20) Wcm (wie mißt man sowas?). Quarzglas (SiO2) soll bei 10 19 Wcm liegen, Phenolharze ("Pertinax") schaffen nur (109 - 10 11) Wcm.
	Ein volles Valenzband und ein mittelgroßes "Bandgap" ergibt Halbleiter. Die thermische Energie bei Raumtemperatur reicht aus, um einigen wenigen Elektronen den Sprung ins Leitungsband zu ermöglichen - etwas Stromleitung kann stattfinden. Wir erwarten, daß die Zahl der Elektronen im Leitungsband und damit die Leitfähigkeit mit wachsender Temperatur stark zunimmt.
		Perfekte Halbleiterkristalle haben bei Raumtemperatur Widerstände von (104 - 10 8) Wcm; Si liegt z.B bei etwa 3 · 105 Wcm; GaAs bei 108 Wcm. Das sind aber keine besonders tiefschürfende Zahlen, da sie stark temperaturabhängig und extrem stark "dreck"abhängig sind. Bei T = 0 K ist die Leitfähigkeit = 0.
	Ein entweder sehr kleines Bandgap, oder ein nicht voll besetztes Valenzband, oder ein Überlapp zwischen vollbesetztem Valenzband und Leitungsband (was man auch als nur teilbesetztes Valenzband auffassen kann) ergibt Leiter, d.h. in der Regel Metalle (bzw. im erstem Fall Halbmetalle). Wir haben (im ersten Fall bei nicht zu kleinen Temperaturen) immer genügend Elektronen, die bewegungsfähig sind.
		Der spezifische Widerstand liegt bei Raumtemperatur im Bereich 10–6 Wcm; z.B rAg  =  1,63 · 10– 6Wcm    (bester Leiter) rCu  =  1,7 · 10– 6Wcm   aber   rMessing = 5,2 · 10– 6 Wcm rZn  =  5.9 · 10– 6Wcm rHg  =  95,8 · 10– 6 Wcm .
	Einfach und sehr flächendeckend. Aber: Wir betrachten nach wie vor perfekte Kristalle. Wie die Bandstruktur eines realen Polykristalls aussieht, der voll ist mit Defekten aller Art, steht noch auf einem anderen Blatt.
		Die typischen Halbleiter Si und Ge wurden früher (ca. 1. Hälfte 20. Jahrhundert) auch eher den Metallen zugerechnet, da ihre Leitfähigkeit so schlecht nicht war. Das war aber eine Folge der zwar faszinierenden, aber nicht so recht faßbaren und deshalb in der deutschen Physik etwas verpönten "Dreckeffekte".
		Diese Dreckeffekte enthalten aber die Grundlagen der Halbleitertechnik, wir werden sie noch ausführlich kennenlernen.
	Wie kann man die Leitfähigkeit eines gegebenen Materials manipulieren? Wie kann man für technische Anwendungen das herstellen, was man braucht?
		Offenbar nur durch gezielte Nutzung der "Dreckeffekte". Die Bandstruktur eines perfekten Kristalls ist was sie ist - die Leitfähigkeit liegt fest und ist allenfalls noch durch die Temperatur beeinflußbar.
		Aber die Temperatur wird bei Isolatoren und Metallen nicht viel vermögen. Die Konzentrationen der beweglichen Elektronen sind dicht an Null oder hoch; viel läßt sich daran nicht ändern.
		Auch Kristallgitterdefekte werden bei Isolatoren und Metallen nicht furchtbar viel tun können. Selbst einige leitende Ausscheidungen in Isolatoren werden die Leitfähigkeit nicht erhöhen, solange keine leitende Pfade zwischen den Ausscheidungen bestehen; und Defekte in Metallen werden zwar die Beweglichkeit etwas herabsetzen, aber das sind verhältnismäßig "kleine" Effekte - maximal 2 Größenordnungen. Das ist klein, wenn man bedenkt, daß die Leitfähigkeit einen Bereich von gut 25 Größenordnungen umfaßt!
	Letztlich erhalten wir für Metalle genau das Verhalten, das wir schon früher besprochen haben. Damit können wir sie hier als abgehakt betrachten. Auch Isolatoren können wir mit Blickrichtung auf die Leitfähigkeit abhaken (sie werden später wieder mit Blickrichtug auf die Dielektrizitätskonstante erscheinen).
		Was bleibt sind die Halbleiter. Sie werden uns für den Rest dieser Vorlesung beschäftigen
		Fragebogen / Questionaire Multiple Choice Fragen zu 4.2.2

© H. Föll (MaWi 2 Skript)