2.3.3 Eigenschaften Fermi-Dirac Statistik und erste Anwendungen

	Zunächst betrachen wir das Grenzverhalten für T Þ 0 K
		Wir bekommen
		Für  E – EF  =  DE < 0 : f(E, 0K) = 1 exp (– ¥) + 1   =  1           Für  E  –  EF  =  DE > 0 :   f(E, 0K) = 1 exp (+ ¥) + 1  =  0
		Das ist genau das, was wir brauchen.
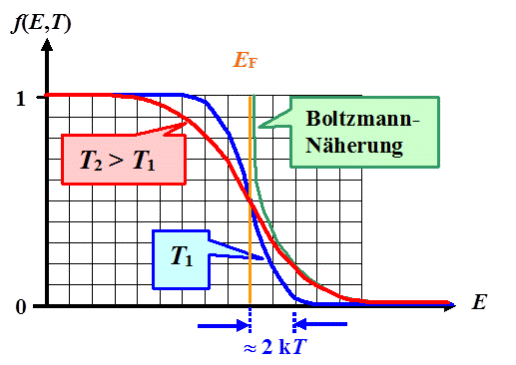
	Es ist nun verhältnismäßig einfach, die Fermiverteilung für eine gegebene Temperatur und Fermienergie auszurechnen. Man erhält eine Kurve wie folgt:
		Das Rechteck bei T = 0 K bekommt mit steigender Temperatur zunehmend eine weiche Flanke; genauso wie wir es vorhersagen konnten.
		Der "weiche" Bereich oder die "Aufweichungszone" hat dabei eine Breite von ungefähr 4 kT. Auch das entspricht der Vorhersage - aber jetzt können wir es ausrechnen; wir wollen das auch in einer Übungsaufgabe tun.
	Wir können weiterhin vermuten, daß der "Hochenergieschwanz" der Fermiverteilung durch die Boltzmannverteilung approximiert werden kann.
		Für E >> EF gilt
		f(E,T)  »  exp  –  E – EF kT
		Das diese Beziehung stimmt, wird ebenfalls in der folgenden Übungsaufgabe gezeigt.
		Übung 2.3-1 Eigenschaften der Fermiverteilung

	Wir wollen eine Grundeigenschaft der Fermieverteilung noch mal wiederholen:
		Sie regelt die Verteilung von Fermionen auf verfügbare Energieplätze im Gleichgewicht. Daraus folgt im Umkehrschluß
		1. Die Fermiverteilung und damit insbesondere die Fermienergie (ein anderes Wort für chemisches Potential) ist nur für das Gleichgewicht überhaupt definiert.
		2. Damit muß im Gleichgewicht die Fermienenergie überall im Material konstant sein.
	Eine weitere, mehr abstrakte Eigenschaft soll noch angesprochen werden:
		Wir haben die Fermienergie definiert als die Energie, bei der f(EF,T) = ½. Damit ist die Wahrscheinlichkeit, daß ein Energieniveau bei der Fermienergie besetzt ist, genau ½.
		Es ist aber grundsätzlich möglich, daß es in der Umgebung der Fermienergie gar kein Energieniveau gibt. In anderen Worten: Die Fermienergie kann ohne weiteres in einem Energiebereich liegen, in dem die Zustandsdichte "zufällig" gerade = 0 ist.
	Oder noch mal anders formuliert: Die Fermiverteilung gibt nur die Wahrscheinlichkeit an, daß die bei der Energie E vorhandenen Plätze besetzt sind. Wie groß die Zahl der Plätze ist, vielleicht sogar Null, hat mit der Fermiverteilung nichts zu tun.
		Die Volumendichte n(E) = N/V der Teilchen die auf den Plätzen bei E sitzen, oder die Zahl N(E) ist immer gegeben durch
		n(E)  =  Dichte der Plätze mal Wahrscheinlichkeit der Besetzung mal Energieintervall         =   D(E) · f(E,T) · DE       N(E)   =   D(E) · f(E,T) · DE · V
	Das ist eine Schlüsselformel! Sie gilt für alle Systeme mit Fermionen! Wir schreiben sie mal genau so pompös auf, wie früher die Boltzmanverteilung:
		Falls ein thermodynamisches System vieler freier Elektronen verschiedene Energiezustände E hat, mit D(E) besetzbaren Plätzen bei E, dann ist im thermodynamischen Gleichgewicht die (differentielle) Teilchendichte d(n(E)) /dE bei der Energie E gegeben durch dn(E)   =  dE · D(E)  · 1  exp æ è Ei  –  EF kT ö ø + 1
		Dabei ist D(E), die Zustandsdichte, eine für das System charakteristische Funktion, und EF, die Fermienergie, eine für das System charakteristische Energie (= Zahl).
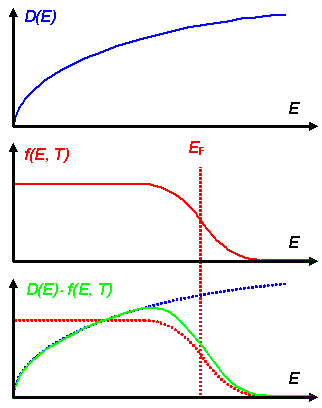
	Die Anwendung dieser Gleichung auf das Modell des freien Elektronengases liefert die folgende Graphik und Formel
		n(E)  =  (2 · me)3/2 · E 1/2 2 · p2 · 3 · ( exp æ è Ei  –  EF kT ö ø + 1)
		Wir erkennen ein gewisses Problem: Obwohl die Materie glasklar ist, und die entsprechenden Graphiken leicht zu konstruieren sind, werden die Formeln schon für den allereinfachsten Fall des freien Elektronengases etwas unhandlich! Das soll uns aber nicht schrecken, denn um mit länglichen Formeln einfach umgehen zu können, haben die Materialwissenschaftler den Si-Chip erfunden und auf Höchstleistung trainiert! Jeder handelsübliche PC oder Laptop mit einem einfachen Matheprogramm macht das mit Links!
	Wir können jetzt sofort die entscheidenden Gleichungen für alles weitere aufschreiben:
		Die Gesamtzahl N bzw. die Dichte n aller Elektronen im System muß per definitionem gegeben sein durch
		n  =  ¥ ó õ 0 D(E) · f(E,T) · dE
		Die Zahl N(E1, E2) bzw. Dichte n der Elektronen, die sich im Energieintervall (E1, E2) befinden, ist entsprechend
		n(E1, E2)  =   E2 ó õ E1 D(E) · f(E,T) · dE
		Die gesamte Energie Eges(E1, E2), die auf die Elektronen im Energieintervall (E1, E2) entfällt ergibt sich damit (pro Volumen) ganz einfach zu
		Eges(E1, E2)  =  E2 ó õ E1 E · D(E) · f(E,T) · dE
		Oben hätte man auch gesamte Energiedichte schreiben können aber dann ist nicht so klar welche Dichte man meint: pro Energieeinheit oder pro Volumen?
	Zum Schluß noch zwei auf den ersten Blick etwas seltsame anmutende Beziehungen, die wir aber noch oft brauchen werden:
		Die Wahrscheinlichkeit wh dafür, daß ein Platz bei der Energie E nicht besetzt ist, wird gegeben durch
		wh  =  1  –  f(E,T)
		Die Dichte n× an "Teilchen", die nicht auf verfügbaren Plätzen sitzen, oder wir könnten auch sagen die Dichte der Nichtteilchen, oder schlicht die Dichte der noch freien Plätze, ist
		n×(E1, E2)  =   E2 ó õ E1 D(E) · (1 – f(E,T) · dE
		Wir schauen uns das noch schnell in einer Graphik an:
	Damit haben wir jetzt ein erstes mächtiges Werkzeug, um den elektronisch bedingten Eigenschaften der Materialien nachgehen zu können.

© H. Föll (MaWi 2 Skript)