2.3.4 Zusammenfassung Kapitel 2.3

	Vorbemerkungen: Hier sind absichtlich keine Links gesetzt. Wer hier etwas nicht sofort versteht, tut gut daran selbst aktiv zu suchen!
	Die Zustandsdichte eines Systems sagt uns, wieviele Plätze in einem gegebenen Energieintervall da sind. Die Frage die wir jetzt stellen ist:
		Wieviele der vorhandenen Plätze sind (mit Elektronen) besetzt?
		Genauer fragen wir: Wie groß ist die Wahrscheinlichkeit f(E,T), daß Plätze bei E besetzt sind.
		Für die Zahl, oder genauer Volumendichte der besetzten Plätze im Intervall n(E1, E1 + DE) gilt dann
		n(E1, E1 + DE)  =   E1 + DE ó õ E1 D(E) · f(E,T) · dE   »   D(E1) · f(E1,T) · DE
		Die letzte Beziehung gilt für DE die so klein sind, daß D(E) und f(E,T) im betrachteten Intervall näherungsweise konstant sind.
	Drei Fragen drängen sich auf:
	1. Ist die Verteilungsfunktion f(E,T) systemspezifisch (wie die Zustandsdicht), oder universell?
		Antwort: f(E,T) ist universell. Sie gilt für jedes fermionische System im thermodynamischen Gleichgewicht.
		Sie ersetzt schlicht die uns (im Prinzip) schon geläufige, ebenfalls universelle Boltzmann Verteilung, die für klassische Teilchen galt.
	2. Wie kann man f(E,T) herleiten?
		Antwort: Mit ziemlich großer Mühe: Wir schreiben die freie Enthalpie des Systems auf - sie wird über die Entropie von der Zahl der Möglichkeiten, die vorhandenen Plätze besetzen zu können abhängen. Die entsprechende Formel enthält also f(E,T); wir haben ein Funktional (eine Funktion, die als "Variable" eine ander Funktion hat).
		Mit Hilfe der Variationsrechnung suchen wir nun diejenige Funktion f(E,T), für die das freie Enthalpiefunktional ein Minimum hat - unter Bachtung der Nebenbedingung Teilchenzahl- und Energieerhaltung!
		Das geht - aber nicht in drei Zeilen!
	3. Was ist das Ergebnis?
		Das Ergebnis ist eine der ganz wichtigen Kurven der Materialwissenschaft: Die Fermi-Dirac Verteilung:
f(E, T)  =  1 exp æ è E  –   EF kT ö ø + 1
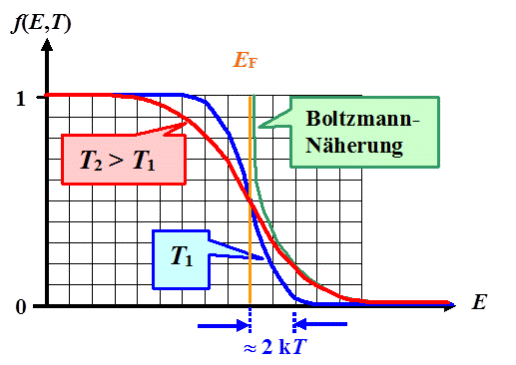
	Die wesentlichen Eigenschaften der Fermi Verteilung sind:
		f(EF,T)   =   ½ Definiert die Fermienergie "Aufweichungsbereich"    »  4 kT   f(E,T)   »  exp – E  –   EF kT    "Boltzmannnäherung" für E > EF
	Daß die Fermieverteilung in etwa so aussehen muß wie sie sich aus der Herleitung ergibt, läßt sich auch durch scharfes Nachdenken ohne Rechnung zeigen.
	Mit (materialspezifischer) Zustandsdichte und (universeller) Fermiverteilung lassen sich einige wichtige allgemeine Formeln hinschreiben:
		Volumendichte n der Teilchen, die auf den Plätzen bei E sitzen, ist immer
		n(E)  =  Dichte der Plätze mal Wahrscheinlichkeit der Besetzung mal differentielles Energieintervall         = D(E) · f(E,T) · DE
		Die Dichte n aller Elektronen im System muß per definitionem gegeben sein durch
		n  =  ¥ ó õ 0 D(E) · f(E,T) · dE
		Die Dichte n der Elektronen, die sich im Energieintervall (E1, E2) befinden, ist
		n(E1, E2)  =   E2 ó õ E1 D(E) · f(E,T) · dE
		Die gesamte Energiedichte, E(E1, E2) die auf die Elektronen im Energieintervall (E1, E2) entfällt ergibt sich damit zu
		E(E1, E2)  =  E2 ó õ E1 E · D(E) · f(E,T) · dE
		Die Wahrscheinlichkeit wh dafür, daß ein Platz bei der Energie E nicht besetzt ist, wird gegeben durch
		wh  =  1  –  f(E,T)

© H. Föll (MaWi 2 Skript)