2.3.5 Merkpunkte Kapitel 2.3

	Fermi-Dirac Verteilungsfunktion			f(E, EF, T) = Wahrscheinlichkeit dafür, daß ein Platz bei der Energie E in einem System mit Fermienergie EF und Temperatur T besetzt ist.
		Damit Wahrscheinlichkeit für Nichtbesetzung		1 – f(E, EF, T)
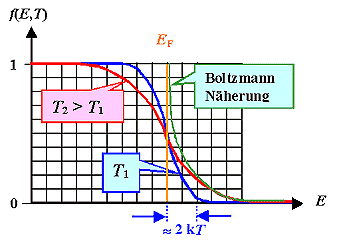
	Die "Fermi Verteilung" oder "Fermi Statistik" hat die nebenstehende Gestalt:			f(E, T)  =  1 exp æ è E  –   EF kT ö ø + 1 f(E, T) »   exp – E  –   EF kT   für E > EF
		f(E, EF, T) ist eine universelle Funktion die für alle fermionischen Systeme im thermodynamischen Gleichgewicht gilt
		Für den "Hochenergieschwanz" darf man die Boltzmannverteilung verwenden
		f(E = EF) = ½ definiert die Fermienergie
		Der "Aufweichungsbereich" liegt in der Größenordnung kT
	Wichtige Formeln sind			n  =  ¥ ó õ 0 D(E) · f(E,T) · dE n(E1, E2)  =   E2 ó õ E1 D(E) · f(E,T) · dE E(E1, E2)  =  E2 ó õ E1 E · D(E) · f(E,T) · dE
		n  =  Gesamtvolumendichte der Elektronen des Systems.
		n(E1, E2)  =  Volumendichte der Elektronen im gegebenen Energieintervall
		E(E1, E2)  =  Gesamtenergie(volumendichte) im gegebenen Energieintervall
	Dies Gleichungen gelten immer, d.h. nicht nur für das freie Elektronengas. Im realen Kristall unterscheidet sich hier nur die Zustandsdichte von der des freien Elektronengases.

© H. Föll (MaWi 2 Skript)