|
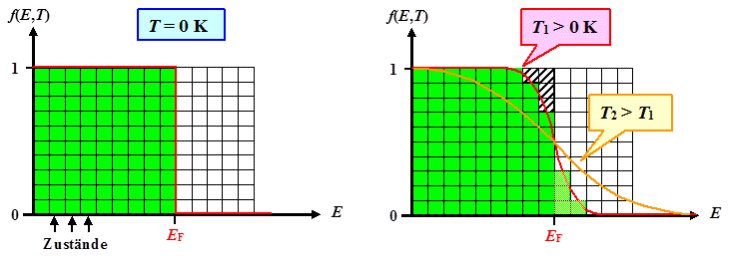
Bei endlicher Temperatur (T > 0K) wird die Besetzung
der möglichen Energieniveaus der freien Elektronen durch die Thermodynamik geregelt. Der Gleichgewichtszustand
des Elektronensystems ist durch das Minimum der freien
Enthalpie G = H – TS gekennzeichnet. |
|
 |
Bei endlichen Temperaturen bedeutet das, daß nicht alle Plätze unterhalb
der (für T = 0 K) definierten Fermienengie besetzt sein können, denn nur so kann Unordnung im Elektronensystem
des Kristalls zustande kommen. |
 |
Was wir gerne wissen möchten ist:
|
|
 |
Mit welcher Wahrscheinlichkeit sind irgendwelche
Zustände bei der Energie E und Temperatur T besetzt, denn mehr als Wahrscheinlichkeitsaussagen
können wir nicht erwarten. |
|
 |
Wir kennen die Antwort auf diese Frage für klassische
Teilchen im Allgemeinen, und für Fermionen, also Teilchen, die dem Pauli Prinzip gehorchen müssen, für den Sonderfall T = 0 K. |
 |
Wir suchen jetzt also die Fermi-Dirac Verteilungsfunktion
f(E, T) für beliebige Temperaturen. |
|
 |
Die Suche ist nicht so einfach; das Ergebnis aber schon. Wir werden die Herleitung hier nicht
schaffen, denn dazu bräuchten wir komplexe mathematische Werkzeuge (Variationsrechnung, Methode der Lagrangen Parameter),
ziemlich viel formale Thermodynamik und ziemlich viel Zeit. |
|
 |
Wir werden aber einige Elemente der Herleitung etwas genauer ansehen, denn dabei kann man
viel über das Wesen des Gleichgewichts im Elektronensystem und über die Eigenschaften der Fermi-Dirac Verteilung
lernen. |
 |
Zunächst überlegen wir uns qualitativ,
wie die Fermi-Dirac Verteilungsfunktion notwendigerweise aussehen muß. |
|
 |
Dazu betrachten wir als Einstieg ein Modellsystem mit konstanter
Zustandsdichte D = 10 eV–1 (wir schenken uns das m –3
in der Dimension) bei T = 0 K und T > 0 K. In diese System stecken wir 90 Elektronen.
Wir könnten auch D = 1011 eV–1 und 1012 Elektronen (oder
jede beliebige ander sinnvolle Kombination) nehmen, aber das muss dann jemand anders zeichnen. |
|
 |
Also immer wieder: Prinzipzeichnungen nicht mit der "Realität" verwechseln! |
|
 |
In jedem Zustand, gekennzeichnet durch eine Energie E, kann man also maximal
10 Elektronen unterbringen. In Diagramm entspricht ein Platz für ein Elektron damit einem Kästchen. |
| |
|
 |
Die Verteilung der Elektronen auf die Zustände bei T
= 0 K ist klar. Alle Zustände bis zur Fermienergie sind besetzt; danach ist alles leer. |
|
 |
Insgesamt gibt es genau eine Möglichkeit, alle 90
Elektronen unterhalb der Fermienergie unterzubringen; oberhalb gibt es ebenfalls genau eine Möglichkeit, die Elektronen
nicht unterzubringen |
|
 |
Wir haben also größtmögliche Ordnung,
da wir nur einen Mikrozustand haben
um die gewünschte Anordung zu realisieren. Das ist gleichbedeutend mit einem Zustand minimaler Entropie. |
 |
Bei einer endlichen Temperatur T1 müssen wir aber
etwas Unordnung erzeugen, um zum Minimum der freien Enthalpie zu gelangen - bei möglichst minimaler Energieerhöhung.
|
|
 |
Dazu müssen wir aus einem besetzten Energieniveau einige Elektronen herausnehmen und
ungern, aber notgedrungen, auf bisher unbesetzte Niveaus bei höheren Energien unterbringen. |
|
 |
Es ist klar, daß wir das bei den höchsten besetzten Energieniveaus machen, und die freigesetzten Elektronen auf
die niedrigsten unbesetzten Niveaus bringen. Qualitativ wird das so aussehen wie mit
der roten Kurve gezeigt - wir haben insgesamt vier Elektronen umgeordnet. Die orange Kurve zeigt das ganze bei höherer
Temperatur und deshalb mit noch mehr Unordnung. |
 |
Wir können aber auch eine quantitative
Aussage dazu machen - wir können nämlich den Grad der erzeugten Unordung und die gesamte Energie für die
gezeigte Anordnung relativ leicht berechnen. |
|
 |
Zunächst müssen wir dazu die Frage beantworten: Wieviele Möglichkeiten PE
gibt es, n (ununterscheidbare) Elektronen auf die NE Plätze bei der Energie
E anzuorden; in unserem Beispiel ist N = 10. Das ist die Frage, die wir uns schon bei der Berechnung
der Leerstellenkonzentration gestellt und beantwortet haben, das
Ergebnis war |
| |
|
 |
Wir haben damit aber erst den Beitrag einer
"Energiesäule", eines Zustands, zur Gesamtentropie. Wir brauchen aber
P, die Zahl aller Anordnungsmöglichkeiten. |
|
 |
Natürlich sagt uns die elementare
Kombinatorik wie das geht, aber man kann sich das ganz schnell auch selbst klarmachen. Wieviele Möglichkeiten gibt
es für die Bildung einer einstelligen Zahl unter der Verwendung der üblichen Ziffern? Richtig, 10 Möglichkeiten.
Für eine zweistellige Zahl? Richtig - 10 · 10. Und so weiter |
|
 |
Wir haben also für P, die Gesamtzahl der Möglichkeiten n
Elektronen auf je N Plätzen bei diskreten Energien Ei zu verteilen |
| |
| P = |
Õ
i |
Ni!
ni! · (Ni – ni)! |
|
|
|
 |
Die Gesamtzahl der Möglichkeiten ist also das Produkt über all die individuellen
Möglichkeiten beim Energieniveau Nr. i, das Ni Elektronen Platz bietet und auf
das wir ni Elektronen verteilen. |
 |
Die Formel gilt natürlich auch für
unser Beispiel, in dem wir Ni = const. = 10 hatten; aber sie ist viel allgemeiner und gilt für
jedes Ni und ni. |
|
 |
Damit können wir die Entropie S für unser Beispiel (und für jedes
andere auch) jetzt berechnen; es gilt wie immer
S = k · ln P |
|
 |
Die Energie E ist sowieso klar, es gilt natürlich E = S
ni · Ei und damit können wir die freie Enthalpie für jede gegebene Anordnung berechnen. Wir haben damit nur nicht die Anordnung mit dem Minimum
der freien Enthalpie gefunden. |
 |
Wir können aber aus dem simplen Beispiel noch weitere Aussagen über
f(E,T) gewinnen. |
|
 |
Die Zahl der Anordnungsmöglichkeiten in einem Energieniveau ist minimal (d.h. = 1)
falls ni = Ni oder ni = 0. Sie ist maximal
für ni = ½ Ni. Das sollte man sich selbst mal in Ruhe überlegen
(oder mit der Stirlingschen Formel und einer Max-Min
Rechnung beweisen). |
|
 |
Das bedeutet, daß wir die bei T = 0 K besetzten Bereiche der Energieniveaus
nie unter einen Besetzungsgrad von ½ sinken lassen werden, denn das würde die Energie ansteigen lassen
bei sinkender Entropie! Wir werden weiterhin versuchen, größtmögliche Entropie bei den höchsten besetzen
Niveaus zu produzieren, d.h. bei der Fermienergie. |
|
 |
Damit ist schon fast zwingend klar, daß unsere Fermi-Dirac Verteilung bei E
= EF den Wert ½ haben wird |
|
|
|
 |
Eine letzte allgemeine Aussage: Die Elektronen, die wir aus Energieniveaus E
< EF herausnehmen, müssen wir bei Energien E > EF wieder
einbauen - denn die Teilchenzahl muß erhalten bleiben. |
|
 |
Und genauso wie wir nur bei den höchsten besetzten Energienieveaus Unordnung machen werden,
wird der Einbau bei den tiefsten nicht besetzten Energieniveaus erfolgen - wir haben
das bereits festgestellt. |
|
 |
Denkt man darüber nach, erkennt man, daß der Fermiverteilung
(wir lassen ab jetzt ungerechterweise Herrn Dirac
weg) keine große Wahl bleibt - sie wird wohl für jede Temperatur T punktsymmetrisch um den Punkt
f(EF, T) herum sein müssen: |
| |
| f(EF + e, T) | = |
1 – f(EF – e, T) |
|
|
 |
Wir können noch eine allerletzte Vermutung äußern: Bei endlichen
Temperaturen steckt im System von der Größenordnung her die (zusätzliche) thermische
Energie kT. |
|
 |
Das ist, so können wir mit einiger Plausibilität vermuten, so ungefähr der
Energiebetrag, um den wir die innere Energie
E bei T erhöhen können, da die zugehörige Entropie die Energieerhöhung über
das –T · S kompensiert. |
|
 |
Das bedeutet aber nichts anderes anderes, als daß die "Aufweichungszone"
in der Fermiverteilung - der Bereich, in dem f(E, T) ¹
0 oder ¹ 1 ist - in der Größenordnung von kT liegen
wird. |
 |
Alles in allem: qualitativ muß
die Fermi-Verteilung so aussehen wie oben eingezeichnet. Bei zunehmenden Temperaturen wird die "Aufweichungszone"
größer, aber solange f(E = 0, T) » 1 gilt, werden
wir f(EF, T) = ½ haben. |
|
 |
Und damit haben wir die Fermiverteilung für endliche Temperaturen schon ganz schön
eingekreist! Wir brauchen jetzt nur noch eine Formel. |
|
| |
|
Zur Berechnung der Fermi-Dirac Statistik |
| | |
 |
Wir brauchen einen Ausdruck, der die freie Enthalpie beschreibt als "Funktion"
der Fermi-Verteilung. Dabei wollen wir auch die Zustandsdichte des zu beschreibenden
Systems verwenden, denn D(E) ist uns jetzt als eine der fundamentalen Funktionen bekannt, die ein Elektronensystem
beschreiben. |
|
 |
Zum "Rechnen" benutzen wir die Formel für die Zustandsdichte des freien Elektronengases;
wenn wir es genau wissen möchten, verwenden wir die richtige, d.h. in der Regel gemessene Zustandsdichte. |
|
 |
Die Zustandsdichte gibt uns letztlich das Ni der obigen Überlegungen
- wir haben aber ein kleines Problem: Bei der Ableitung der Zustandsdichte über den Phasenraum, haben wir stillschweigend
aus diskreten Energieniveaus ein Kontinuum gemacht; es wurde des öfteren schon als "Quasikontinuum"
angesprochen. |
|
 |
Wir müssen, um die Kombinatorikformeln verwenden zu können, jetzt wieder diskrete Energieniveaus, gekennzeichnet durch den Index "i" einführen,
und das tun wir indem wir alle Zustände in einem festen Energieintervall DE
der in der Mitte des Intervalls sitzenden Energie Ei zuschreiben. |
|
 |
Aus der Definition der Zustandsdichte D(E) haben wir |
| |
| D(Ei) | = | 1
V |
· | dN(E)
dE |
» | 1
V | · |
DN(E)
DE |
|
|
|
 |
Damit können wir die Zahl
Ni der Plätze für Elektronen auf dem artifiziellen
Energieniveau bei Ei wie folgt schreiben |
|
|
| Ni = DN(Ei) =
V · D(Ei) · DEi |
|
|
|
 |
Wir können also die Formeln wie oben geschrieben verwenden, müssen
dann aber gelegentlich Ni durch V · D(Ei) ·DE ersetzen. Das Ganze ist im wesentlichen nur ein mathematischer Trick, denn wir
müssen für die diversen Näherungen, die wir später brauchen werden, sicherstellen, daß Ni
nicht zu klein wird. Hier steckt aber, und das sei deutlich gesagt, ein Stückchen Willkür. Allerdings spielt diese
Willkür im Endergebnis keine Rolle - wir werden sehen. |
 |
Wir schreiben nun den Energie- und Entropieterm mit Hilfe der
Fermi Verteilung. Dazu müssen wir nur ni ersetzen durch Ni · f(EF,
T). |
|
 |
In Worten, weil das so wichtig ist: Die Zahl ni
der Elektronen, die Ni Plätze bei der Energie E und Temperatur T
besetzen, ist gleich der Zahl Ni der vorhandene Plätze mal der Wahrscheinlichkeit, daß sie besetzt sind.
|
|
 |
Damit erhalten wir für Entropie und Energie |
| |
| S = k · ln P = | k · ln |
Õ
i | |
æ
ç
è |
Ni!
ni! · (Ni - ni)! |
ö
÷
ø |
= k · ln |
Õ
i | |
æ
ç
è |
Ni!
{Ni · f(Ei,
T)}! · {Ni - Ni · f(Ei, T)}! |
ö
÷
ø |
|
|
 |
Damit können wir die freie Enthalpie G = E – TS
hinschreiben - wir verzichten aber darauf, das ganze sieht auch so schon schön schaurig aus. |
|
 |
Wie geht es weiter? Die freie Enthalpie hängt jetzt von einer unbekannten
Funktion ab; sie ist ein Funktional. Wir suchen die spezielle Funktion f(E,
T), für die G(E, T) ein Minimum wird. |
|
 |
Das ist die gute alte Minimum-Maximum Kurvendiskussion auf einer höheren Ebene - die
zugehörige mathematische Disziplin heißt Variationsrechnung und führt
nicht auf algebraische Gleichungen, sondern auf Differentialgleichungen. |
|
 |
Wer das in Mathe nicht gelernt hat (oder schon wieder vergessen hat) schaut schnell im "Feynman" nach (Band II, Kapitel 19). |
 |
Aber das Prinzip ist ganz einfach: Wir "wackeln" ein bißchen an
G, und schauen, wie G darauf reagiert. |
|
 |
Das "Wackeln" macht man, indem man die Variablen in G differentiell
ein wenig ändert. Ändere ich zum Beispiel die Zahl ni der Elektronen im E-Niveau
Ei ein wenig, wird sich die Änderung oder Variation dG
von G nach den allgemeinen Prinzipien der Differentialrechnung so darstellen: |
| |
|
|
 |
Wir benutzen ein extra Zeichen (das "d") für
"Variation", aber es ist im Grunde nichts anderes als das totale Differential. |
 |
Die entscheidende Erkenntnis ist nun: Falls dG
¹ 0 ist, haben wir kein Minimum. Denn das bedeutet,
daß die freie Enthalpie sich vergrößert oder verkleinert, falls wir die Teilchenzahl im i-ten Niveau
etwas ändern; G kann also nicht im Minimum sein. |
|
 |
Das gilt für alle i; die Forderung nach dem Minimum der freien Enthalpie ist also |
| |
| dG = |
S
i |
¶G
¶ni |
· dni | = 0 |
|
|
|
 |
Das ist im übrigen nicht neu - wir hatten das schon in etwas anderem Zusammenhang. |
 |
Wir gehen jetzt aber einen Schritt weiter, und schauen uns das Ganze im einfachst
möglichen Modellsystem an - ein Gebilde mit nur zwei
E-Niveaus, d.h. i "läuft" von 1 bis 2 |
|
 |
Damit gilt für das Gleichgewicht |
| |
¶G
¶n1 |
· dn1 |
= – |
¶G
¶n2 |
· dn2 |
|
|
|
 |
Das reicht aber noch nicht, denn wir müssen zusätzlich berücksichtigen,
daß die Elektronenzahl konstant ist. Was ich aus Niveau 1 herausnehme,
muß ich in Niveau 2 hineintun, und umgekehrt. Wir haben also als Nebenbedingung |
| |
|
 |
Daraus folgt sofort als andere Form der Gleichgewichtsbedingung: |
| |
¶G
¶n1 | = |
¶G
¶n2 | = const. = µ |
|
|
|
 |
Die das Gleichgewicht charakterisierende Größe µ heißt "Chemisches Potential" - auch das hatten wir schon. Wir können jetzt schnell von 2
E-Niveaus auf beliebig viele verallgemeinern: Da wir ohne Beschränkung der Allgemeinheit alle dn2
bis auf zwei immer = 0 setzen können, muß im Gleichgewicht immer gelten |
| |
|
 |
Das hat eine überaus wichtige Konsequenz
für uns: Die Gleichung sagt, daß das chemische Potential der Elektronen in allen Energiezuständen überall im Kristall gleichgroß sein muß. |
|
 |
Das "überall im Kristall" bezieht sich
jetzt explizit auf den Ort. Egal wo die Elektronen sich herumtreiben, ihr chemisches
Potential ist im Gleichgewicht überall dasselbe. |
|
 |
Big Deal! Was nützt das? Woher kennt man das chemische Potential und was nützt dieser
Spruch? - Geduld; wir kommen gleich dazu. |
 |
Wir könnten jetzt zur Lösung der Variationsaufgabe schreiten, wobei
wir nicht nur die Formel für die freie Enthapie in voller Schönheit aufschreiben und differenzieren müßten,
sondern auch noch Teilchenzahlkonstanz (und darüberhinaus noch Gesamtenergiekonstanz
bei der gewählten Temperatur) als Nebenbedingungen
berücksichtigen müssen. |
|
 |
Das kann man zwar mit der Methode der "Lagrangeschen
Parameter" relativ elegant machen; aber der Rechenaufwand ist doch ziemlich
heftig; außerdem muß man noch ein paar tiefe Kenntnisse thermodynamischer Zusammenhänge hineinstecken.
Wir springen deshalb direkt zum Ergebnis und erhalten eine der wichtigsten Formeln der Materialwissenschaft und Physik |
| |
ni =
|
Ni ·
|
1
|
| exp |
æ
è |
Ei – µ
kT |
ö
ø |
+ 1 |
|
|
|
 |
In Worten: Die Zahl
ni (oder, fallls wir durch das Volumen V dividieren, die
Volumendichte) der Elektronen die im thermodynamischen Gleichgewicht Ni Plätze
(oder Platzdichten) bei der Temperatur T besetzen, ist gleich der Zahl
(oder Dichte) der vorhanden Plätze mal einer Funktion, die als Variablen nur die
Energie Ei der betrachteten Plätze und die Temperatur T enthält sowie als
Parameter das chemische Potential µ des betrachteten Systems. |
 |
Darüber hinaus erhalten wir noch eine weitere wichtige Beziehung die zwar
nicht ganz allgemein gilt, aber für alle uns interessierende Fälle sehr gut stimmt: |
| |
|
|
 |
Dabei ist mit EF durchaus die für T = 0 K
definierte Fermienergie gemeint, also eine wohldefinierte Größe.
|
|
 |
Wir sind also das chemische Potential, das uns leichtes
Unbehagen verursacht, schon wieder losgeworden. Allerdings auf Kosten der ganz großen Allgemeinheit, da die obige
Gleichung nicht in voller Strenge gilt, sondern nur für die uns hier interessierenden Fälle. Mehr zum chemischen
Potential findet man in einem eigenen Modul |
 |
Vergleichen wir das Ergebnis mit der Definition der Fermi Verteilung
wie sie implizit in einer der obigen Formeln steckt, erhalten wir das Endergebnis |
| |
f(E, T) =
|
1
|
| exp |
æ
è |
E – EF
kT |
ö
ø |
+ 1 |
|
|
|
Einige Bemerkungen zur Fermiverteilung und
ihrer Herleitung |
| |
|
 |
Die Fermiverteilung enthält nicht
DE, das etwas willkürlich gewählte Energieintervall,
um vom Quasikontinuum der Energiezustände in der Zustandsdichte zu diskreten Niveaus zu kommen. |
|
 |
Wir haben damit also kein Problem mehr, die Fermiverteilung gilt willkürfrei
ganz allgemein und in voller Strenge. |
 |
Die mathematische Form der Fermiverteilung ist die einfachste Formel, die man sich denken kann um eine Funktion zu beschreiben, die bei T
= 0 K sprungartig von 1 auf 0 übergeht, bei endlichen Temperaturen aber "sanft", wie oben
qualititativ gezeigt. Sie hat einfach all die Eigenschaften, die wir uns schon qualitativ klar
gemacht haben. |
|
 |
Es dürfte schwer sein, eine einfachere Formel zu finden, die diesen Sachverhalt ausdrückt. |
|
 |
Wir müssen Mutter Natur also dankbar sein, daß sie den mathematischen Aufwand minimiert
hat. Daran wollen wir uns erinnern, wenn wir die mathematischen Tücken zu spüren bekommen, die dann schon noch
kommen werden. |
 |
Mit der Fermiverteilung können wir die Fermienergie
EF jetzt neu definieren: |
|
 |
EF folgt aus |
| |
|
|
 |
Auch das haben wir uns schon qualitativ überlegt. Diese
Definition ist viel allgemeiner als die alte Definition, nach der Fermienergie
identisch ist mit der Energie des bei T = 0 K letzten besetzten Platzes. |
|
 |
Beide Werte für EF sind aber für halbwegs "normale"
Kristalle identisch, wie wir im nächsten Unterkapitel sehen werden. Für die Ausnahmen
gibt es einen eigenen Modul. |
| |
|
© H. Föll (MaWi 2 Skript)