|
In unserem Modell des freien Elektronengas haben wir diskrete Energieniveaus bekommen,
mit Energiewerten die wir ausrechnen konnten. |
|
 |
Zu einem Energieniveau können – je nach Entartungsgrad – mehrere
Zustände gehören. Wieviel genau, können wir exakt ausrechnen (im Zweifelsfall,
wie gezeigt, durch die Abzählerei bzw. Kombinatorik) oder mit Hilfe der
Zustandsdichte
D(E) in sehr guter Näherung approximieren. |
|
 |
Denn die Volumendichte
ze(E) der Elektronenzustände und die Zahl
der Elektronenzustände g(E) im Energieintervall DE
war |
|
|
| ze(E) | = |
D(E) · DE
| | | |
| | g(E) |
= |
L3 · D(E) · DE |
|
|
 |
Wir müssen jetzt nur das Energieintervall DE
gleich dem (minimalen) Abstand der diskreten Energienieveaus machen um die Zahl der
Zustände zu E (d.h. den Entartungsgrad) zu bekommen. Im freien Elektronengasmodell nehmen
wir also
|
| |
| DE = |
 2 2
2me |
æ
ç
è |
2p
L |
ö
÷
ø |
2 |
|
|
|
 |
Die Unterscheidung zwischen Zahl und Volumendichte
an Zuständen, Elektronen, oder sonstigen Teilchen ist trivial und lästig. Oft sagt und schreibt man auch gar nicht
mehr immer, was eigentlich gemeint ist – es ergibt sich zweifelsfrei aus dem Kontext oder spätestens bei einem
Check der Maßeinheiten. Im Kontext dieses Unterkapitels muß man allerdings genau hinschauen,
wie wir gleich sehen werden. |
 |
Unser ein Elektron hat also viele Möglichkeiten
sich einen Zustand, und damit verkoppelt eine Energie auszusuchen – die Frage ist, ob wir vorhersagen können,
welche der Möglichkeiten unter den gegebenen Umständen realisiert werden. |
|
 |
Eine berechtigte Frage mit einer simplen Antwort: Ein Elektron wird auf dem energetisch niedrigsten
Niveau sitzen.Wir wollen aber nicht nur ein Elektron betrachten, sondern viele.
Dann wird die Sache komplexer. |
|
 |
Wir haben bereits überlegt, daß das
freie Elektronengasmodell sich nicht ändert, wenn wir nun viele Elektronen "einfüllen"; aber unsere
Fragestellung ändert sich etwas: |
 |
Zwar haben unsere vielen Elektronen nach wie
vor viele Möglichkeiten sich jeweils einen Zustand, und damit verkoppelt eine Energie auszusuchen, aber mit der Eingrenzung,
daß alle diejenigen Zustände "tabu" sind, die bereits von einem anderen Elektron besetzt werden –
das Pauli-Prinzip schlägt zu! |
|
 |
Die Frage ist jetzt, ob wir vorhersagen können, wie sich die vielen
Elektronen auf die Zustände und damit auch auf die Energien verteilen. |
|
 |
Wie immer, können wir für Systeme mit vielen Teilchen nur statistische oder Wahrscheinlichkeitsaussagen
machen. Wir fragen also nun ganz präzise |
 |
Wie groß ist die Wahrscheinlichkeit dafür, daß
ein Zustand, d.h. ein Energieniveau mit der Energie E mit Elektronen besetzt ist? |
|
 |
Wir haben uns diese Frage in leicht verschiedenem Kontext schon einmal gestellt, als wir nach der Wahrscheinlichkeit fragten, mit der eine Leerstelle oder ein beliebiges
diffundierendes klassisches Teilchen, eine Energiebarriere der Höhe E überwindet.
|
|
 |
Das war gleichbedeutend mit der Frage mit welcher Wahrscheinlichkeit dieses Teilchen ein Energieniveau
bei E besetzt, und führte auf die Boltzmannverteilung
|
| |
|
|
 |
Mit N(E) = Zahl der Teilchen mit der Energie E, und N0
= Gesamtzahl der Teilchen (wobei immer N << N0 unterstellt ist). |
|
 |
Aber das war für klassische Teilchen, die prinzipiell
unterscheidbar waren und von denen beliebig viele auf einen
Zustand passen – es gibt kein Pauli-Prinzip. |
|
 |
Wir hatten die Formel auch nicht hergeleitet, sondern postuliert
und nur festgehalten, daß diese Verteilung für klassische Teilchen immer
die freie Enthalpie bzw. Energie minimiert. |
 |
Wir hatten außerdem keine Aussagen darüber gemacht, wieviele
Plätze es bei einer gegebenen Energie eigentlich gibt. Zunächst könnte man auch meinen, das sei egal –
ich kann immer beliebig viele klassische Teilchen auf einem Energieplatz unterbringen – was sollte sich ändern,
wenn es viele Plätze gibt? |
|
 |
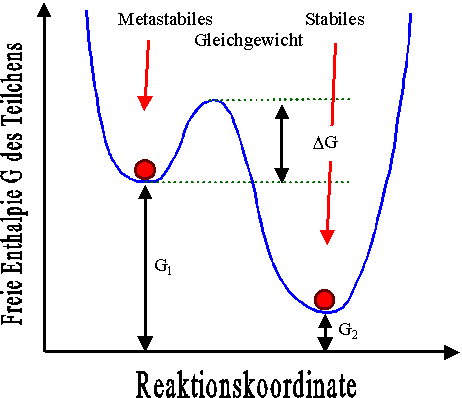
Dass es ganz so einfach nicht ist, wird sofort klar, wenn wir uns das im Matwiss I eingeführte Modellsystem mit zwei Minima der freien Enthalpie
etwas genauer betrachten: |
| |
|
 |
Die finale Aussage
dazu war: |
|
 |
"Falls ein thermodynamisches System verschiedene
angeregte Energiezustände Ei relativ zum Grundzustand E hat (mit E0
= Zustand mit der kleinsten Energie := 0), dann ist die Zahl der Teilchen Ni bei der
Energie Ei gegeben durch Ni = N0·exp–( Ei/kT).
Dabei dürfen wir in guter Näherung N0
» Gesamtzahl der Teilchen setzen, falls Ni << N0
gilt." |
 |
Daran ist auch nichts falsch – aber für etwas kompliziertere Systeme
mit Energieentartung müssen wir schon den Entartungsgrad oder, was fast dasselbe
ist, die Zustandsdichte mit berücksichtigen. |
|
 |
Denn der Trick an der Sache war ja, dass eben nicht alle Teilchen bei der kleineren Energie
sitzen, obwohl das nicht verboten ist. Die Entropie wäre zu klein. Durch die Anordnung einiger Teilchen auf einem andern
Zustand kann man die Unordnung vergrößern, bezahlt dafür aber mit höherer innerer Energie. |
|
 |
"Irgendwie" müßte dabei aber schon die Zahl der Plätze eingehen.
Tut es auch – wir haben nur bisher immer stillschweigend angenommen, dass es immer gleichviele sind. |
|
 |
Da das aber hier von untergeordneter Bedeutung ist, betrachten wir mehr Details dazu in einem
eigenen Modul. |
|
| |
|
Die Fermi-Dirac-Verteilungsfunktion
bei T = 0 K |
| |
|
 |
Was wir jetzt wissen wollen ist: Wie groß
ist die Wahrscheinlichkeit dafür, daß ein Energieniveau mit der Energie E mit einem Elektron,
d.h. mit einem nicht-klassischen Teilchen besetzt ist, für das das Pauli-Prinzip gilt? |
|
 |
Diese Wahrscheinlichkeit muß von der Energie E und der
Temperatur T abhängen; wir nennen sie nach den "Entdeckern" die Fermi-Dirac-Verteilungsfunktion
oder Fermi-Dirac-Statistik oder einfach Fermistatistik
f(E,T)
(Die Menschen im allgemeinen sind ungerecht, im besonderen selbst bessere Menschen,
wie Physiker und Materialwissenschaftler: Niemand kennt die Nr. 2! Wer hat nach Neils Armstrong als zweiter den Mond betreten?
Die Frage nach Nummer 3 war im übrigen die 1.000.000-€-Frage in einer Fernsehshow im April 2005; es wurden sogar
4 Namen zur Auswahl gegeben). |
|
 |
Genau wie bei der Boltzmannverteilung fordern wir, daß eine Verteilung der Elektronen
nach der Fermistatistik automatisch zum Minimum der freien Energie F
= E – T · S (oder Enthalpie) führt; oder anders ausgedrückt: Im thermodynamischen
Gleichgewicht sind die Elektronen nach der Fermistatistik verteilt. |
 |
Das Pauli-Prinzip macht die Sache im Grunde einfach, denn für T
= 0 K können wir f(E,T) sofort angeben: |
|
 |
Da der Entropiebeitrag zur freien Energie/Enthalpie dann keine Rolle spielt, müssen wir
jetzt nur die Energie minimieren, und das können wir dann und nur dann, wenn wir
alle verfügbaren Plätze "von unten her", d.h. bei der kleinsten Energie beginnend nacheinander auffüllen.
Dabei kommt auf jeden Zustand genau ein Elektron. Klassische Teilchen hätten wir
natürlich alle auf das tiefste Niveau gesetzt. |
|
 |
Bei einer endlichen Zahl von Elektronen ist irgend wo
dann auch das letzte Elektron untergebracht, und das "wo
" bezieht sich dabei sowohl auf die Quantenzahlen des letzten zu besetzenden Zustandes als auch auf die zugehörige
Energie. Dazu wiederholen wir jetzt eine eminent wichtige Definition: |
 |
Die Energie des letzten besetzten Zustandes
bei T = 0 K heißt Fermienergie EF .
|
|
 |
Damit haben wir wieder die absolute Schlüsselgröße
aller elektronischen Eigenschaften von Festkörpern eingeführt – mit einer noch etwas naiven Definition von
EF. Wir wollen uns diese Definition zwar gut merken, aber möglichst bald durch eine bessere
Definition ersetzen. |
|
 |
Die Fermienergie wird also sowohl von der Art und Verteilung der
(Energie)zustände
abhängen, als auch von der Anzahl der unterzubringenden Elektronen. |
|
 |
Damit können wir die Fermistatistik für T = 0 K leicht
graphisch darstellen: |
| |
|
|
 |
Unterhalb der Fermienergie EF sind alle Zustände mit Sicherheit
besetzt, d.h. f(E,T) = 1; oberhalb EF sind
alle Zustände mit Sicherheit nicht besetzt (oder "leer"), d.h. f(E,T) = 0. |
 |
Wir haben eine klare Besetzungsschematik, die nicht nur minmale Energie liefert,
sondern gleichzeitig größtmögliche Ordnung. Denn es gibt eben nur eine einzige Anordnungsmöglichkeit P zu diesem Zustand (die Vertauschung zweier
Elektronen bringt nichts, da wir sie nicht unterscheiden können). |
 |
Aus dem Spezialfall T = 0 K können wir noch viel Honig saugen,
bevor wir zum allgemeinen Fall beliebiger Temperaturen übergehen. Als erstes wollen wir nochmals
die Fermienergie berechnen. |
|
 |
Das ist einfach. Wir betrachten ein Material, das die Zustandsdichte des freien Elektronengases
hat, und das über N0 freie Elektronen verfügt. Diese müssen wir auf die verfügbaren
Energiezustände unterbringen, das Energieniveau des letzten untergebrachten Elektrons definiert die Fermienergie.
|
|
 |
Wir müssen also nur in die bereits abgeleitete
Formel für die Zahl der Zustände N(E) bis zur Energie E, N0
und EF einsetzen und nach EF auflösen um für die Fermienergie
(des freien Elektronengases) zu finden |
|
|
| EF = |
 2 2
2me |
æ
ç
è |
3p
2 · N0
V |
ö
÷
ø |
2/3 | = |
 2 2
2me |
æ
ç
è |
3p2 · ne |
ö
÷
ø |
2/3 |
|
|
 |
Das ist schon eine ganz brauchbare Formel – sie enthält keinerlei Unbekannten
mehr – und im übrigen hatten wir sie schon! Für Alkalimetalle,
zum Beispiel, wissen wir, daß wir genau ein freies Elektron pro Atom haben. Die
Dichte an freien Elektronen ne = N 0 / V ist also bestens bekannt und wir können
die Fermienergie ausrechnen. |
|
 |
Wie sinnvoll wäre das? Nun, das war Inhalt der Übung
2.2-2. Es ist schon sinnvoll (Übung ansehen!) aber nicht besonders, aus zwei Gründen:
- Haben wir keine Ahnung, wie gut die Zustandsdichte des freien Elektronengases die wahre Zustandsdichte eines Alkalimetalls
repräsentiert, und
- Wir haben einen ziemlich willkürlichen Nullpunkt unserer Energieskala gewählt. Das Ergebnis – in eV
– ist genauso willkürlich.
|
 |
Zum ersten Punkt sind uns die Hände gebunden – wir werden weder jetzt
noch später bessere Zustandsdichten rechnen können – aber das zweite Problem läßt sich leicht
beheben. |
|
 |
Dazu nehmen wir unser altes Potentialtopfmodell
für das freie Elektronengas und definieren einen neuen Nullpunkt
für die Energieachse: |
|
|
|
|
 |
Rechts sind die Energieniveaus eingezeichnet, die wir zwischenzeitlich ausgerechnet haben;
der blaue Kasten symbolisiert das Quasikontinuum, das sich bei etwas höheren Energien ergibt (und das auch oberhalb
der roten Linien auch noch da wäre). Die Fermienergie als letztes besetzes Niveau (immer noch bei T = 0 K)
ist als gelbe Linie markiert. Die rote Linie definiert unseren neuen Energienullpunkt
. |
|
 |
Es ist die "Vakuumenergie" der
Elektronen, d.h. die Energie die man gewinnt, wenn man aus dem "Vakuum", d.h. von weit her, ein Elektron auf eines
der Niveaus im Kristall setzt. Umgekehrt ist es genau die Energie, die man braucht um ein Elektron vom Inneren des Kristall
ins "Unendliche" zu bringen. |
 |
Damit ist die Bedeutung der Fermienergie schlagartig klar: Es ist die kleinstmögliche Energie, die man braucht, um ein Elektron aus dem Kristall ins "Unendliche" zu bringen.
|
|
 |
Für ein einzelnes Atom war das schlicht die Ionisierungsenergie
I, für einen ganzen Kristall (oder jeden beliebigen Festkörper) nennen wir diese Energie "Austrittsarbeit
"; oft abgekürzt mit "W"
(für das englische "Workfunction"). |
|
 |
Im Moment könnten wir statt "Austrittsarbeit" auch Fermienergie sagen - aber
wir werden noch sehen, daß das Konzept der Fermienergie tiefer geht als die Definition einer Meßgröße
– denn mehr ist die Austrittsarbeit erst mal nicht. |
|
 |
Die Austrittsarbeit bezieht sich auf einen Kristall, und die Ionisierungsenergie bezieht sich auf die einzelnen
Atome der Basis des Kristall; die Zahlenwerte
werden also unterschiedlich sein – aber wohl nicht sehr! Damit kennen
wir die Größenordnung der Fermienergie in einem System mit der Vakuumenergie als Nullpunkt der Energieskala
(und dem "Pfeil" der positiven Energierichtung nach unten): Sie wird so zwischen (2 ... 25) eV liegen. |
 |
Zum Schluß betrachten wir noch die Zustandsdichte bei der
Fermienergie; auch dafür haben wir bereits die passende Formel. |
| |
|
|
 |
Wir haben N 0 in der Formel weil eben bei der Fermienergie alle N
0 Elektronen untergebracht sind. |
© H. Föll (MaWi 2 Skript)