|
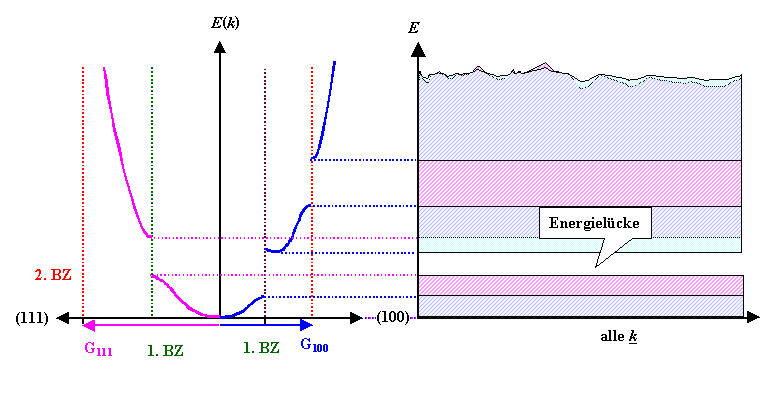
Wichtig ist, das folgende Bild in allen Details zu verstehen: |
| |
|
|
 |
Links eine reale Dispersionskurve. Der wesentliche Unterschied
zu den aus freiem Elektronengas + Beugung konstruierten Kurven ist:
- Die Größe der Energielücke (weiterhin auf Rändern der Brillouinzone) ist wohldefiniert und für
einen gegebenen Kristall gegeben (und tabelliert).
- Der Verlauf der Dispersionskurve zwischen 2 Brillouinzonen kann deutlich von der freien Elektronengasparabel
abweichen, insbesondere müssen die Maxima und Minima nicht immer auf den Rändern
der BZ liegen.
|
|
 |
In jeder reziproken Gitterrichtung sieht die Dispersionskurve anders aus. Aus allen
Dispersionkurven läßt sich das stark abstrahierende Banddiagramm bilden.
Je nach Ausprägung der Dispersionkurven findet man eine Energie- oder Bandlücke mit einer mehr oder weniger großen Bandlückenenergie EG
("G" steht für engl. "Gap" = Lücke). |
 |
Die Zahl der Zustände in einem Ast der Dispersionskurve (der Bereich zwischen
zwei BZ) ist genau die Zahl der Elementarzellen des Gitters. |
|
 |
Die Zahl der auf die Zustände zu verteilenden (mehr oder weniger freien, d.h. durch Bandstrukturen
zu beschreibenden) Elektronen ist damit Zahl der EZ mal Zahl der durch die Atome der Basis eingebrachten freien Elektronen. |
|
 |
Damit steht im Prinzip fest, wieviele Bänder man braucht um alle
(freien) Elektronen unterzubringen. |
|
 |
Das letzte mit Elektronen (voll- oder teilbesetzte) Band heißt Valenzband,
das darüberliegende (leere) Band Leitungsband. |
 |
Die Zustandsdichte muß ebenfalls modifiziert werden.
|
|
 |
In der Bandlücke des (perfekten!) Kristalls ist die Zustandsdichte per definitionem =
0. |
|
 |
Entlang eines Astes einer Dispersionskurve sind die nötigen Modifikationen zwar nicht
dramatisch; in einem aus der Überlagerung vieler Äste gewonnenem Band kann
die Zustandsdichte dann aber aber ziemlich bizarr werden. |
|
 |
Reale Zustandsdichten sind deshalb für analytische Formeln nicht mehr geeignet; entweder
muß man jetzt nähern oder numerisch rechnen. |
 |
Die Banddiagramme realer Kristalle erlauben einfache Definitionen von Materialklassen: |
|
 |
Da in "vollen" Bändern (d.h. alle vorhandenen Zustände sind mit Elektronen
besetzt) die dort "sitzenden" Elektronen ihren Zustand grundsätzlich nicht ändern können, tragen
volle Bänder nicht zur Leitfähigkeit bei. Damit ergibt sich folgende Klassifikation: |
|
 |
Metalle (und Halbmetalle)
sind Materialien mit Bandstrukturen die entweder keine oder nur eine kleine (EG
£ 0,5 eV) Bandlücke haben. |
|
 |
Halbleiter sind Kristalle mit voll besetztem Valenzband
und einer Bandlücke im Bereich von 0,5 eV EG
£ 2,5 eV. |
|
 |
Isolatoren sind Kristalle mit voll besetztem Valenzband
und EG ³ 2,5 eV. |
© H. Föll (MaWi 2 Skript)