|
In vorhergehenden Unterkapitel haben wir uns klar gemacht, daß wir bei einer
Übertragung des freien Elektronengasmodells auf Kristalle in einer ersten Näherung nur bei den Wellenvektoren,
die der Bragg-Bedingung genügen, Änderungen im Verhalten der zugehörigen Elektronenzuständen erwarten
müssen. |
|
 |
Jetzt müssen wir uns fragen: Welche Wellenvektoren sind das denn? Wir nennen
sie mal kB. |
|
 |
Schön wäre eine simple Formel oder Konstruktion, die für ein gegebenes Gitter
die betroffenen Wellenvektoren kB aus der Menge aller möglichen Wellenvektoren k
heraussiebt. |
 |
So etwas gibt es, wir betrachten dazu die Brillouin
Konstruktion der Beugung. So wie die Ewald Konstruktion uns einfach
zeigt, was sich für die Beugung im Falle eines fixen Wellenvektors und eines variablen Gitters ergibt, zeigt uns die Brillouin Konstruktion, was man für ein fixes Gitter und variable Wellenvektoren erhält. |
|
 |
Im Prinzip können wir alle Wellenvektoren, die als Lösung der Schrödingergleichung
für das freie Elektronengas auftreten, in das reziproke Gitter einzeichnen; wir wollen also auch hier das reziproke
Gitter als Darstellungsraum für die Brillouin Konstruktion wählen. |
|
 |
Alles was wir dann noch zu tun haben ist, auf jede Strecke, die vom Ursprung zu
einem reziproken Gitterpunkt führt, die Mittelhalbierende zu zeichnen. Zweidimensional
ist das eine Strecke, dreidimensional eine Fläche. |
|
 |
Alle Wellenvektoren, die auf einer dieser Flächen enden, erfüllen
die Bragg-Bedingung! |
 |
Das schauen wir uns in einer simplen Graphik eines zweidimensionalen Gitters an;
die obige Aussage ist dann elementar zu beweisen. |
|
|
|
|
 |
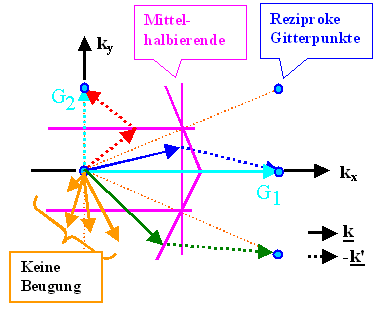
Direkt sichtbar ist, daß jeder k-Vektor, der auf einer der rosa
Mittelhalbierenden endet, einen Wellenvektor k' produzieren "darf", der die Bragg-Bedingung
k – k' = G erfüllen kann. Eingezeichnet sind der Einfachheit
halber die –k Vektoren. |
|
 |
Dreidimensional haben wir Flächen - und diese Flächen werden sich schneiden und
ein System von ineinandergeschachtelten Polyedern bilden. Das kleinstmögliche Polyeder
ist natürlich nichts anderes als die Wigner-Seitz
Elementarzelle des reziproken Gitters! |
 |
Wir führen jetzt einen alternativen Namen für die Wigner-Seitz Elementarzelle
des reziproken Gitters ein, wir nennen sie die erste
Brillouin Zone, abgekürzt 1. BZ. |
|
 |
Das hat keinen tieferen Grund, sondern macht nur die Systematik leichter: Nach der 1. BZ kommt die 2.
Brillouin Zone, danach die 3. BZ und so weiter - wir betrachten einfach die sich
ergebende Abfolge von ineinandergeschachtelten Polyedern, die sich automatisch ergibt, wenn man das Mittelhalbierenden-Rezept
konsequent fortsetzt. |
|
 |
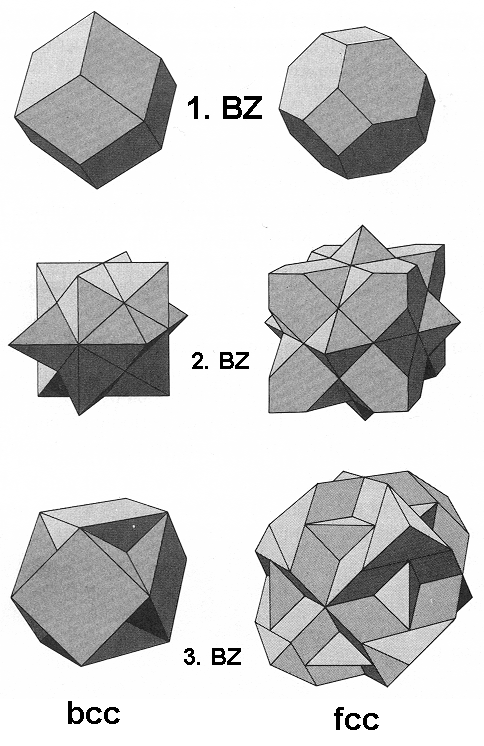
Leicht gesagt, nicht ganz so leicht dreidimensional durchgeführt. Aber schon früh
hat man Doktoranden gequält und perspektivische Zeichnungen erstellen lassen - in diesem Fall war es 1965 Herr
Lück (und damals gab es noch keine Computergraphik!). |
| |
|
|
 |
Es ist schon ganz erstaunlich, wie man von einem einfachen Würfel durch sukzessive Anwendung
eines einfachen Rezepts zu recht komplizierten Edern kommt. Aber das soll uns nicht stören; niemand muß diese
Strukturen auswendig können. |
 |
Wir sehen jedoch eine erste
Konsequenz für die Darstellung von Funktionen im k- Raum: |
|
 |
Die beim freien Elektronengas noch vorhandene Kugelsymmetrie geht verloren, dafür bekommen wir Symmetrielemente des Gitters. |
|
 |
In anderen Worten: Bisher war es völlig egal, in welche exakte Richtung im k-
Raum die k- Achse zeigte, Funktionen wie E(k) oder D(k)
sahen immer gleich aus. |
|
 |
Jetzt schneidet eine beliebige k- Achse eine Brillouin Zone nach der
anderen - und wo diese Schnittpunkte liegen hängt von der Richtung von k
ab und damit davon, in welche Richtung im reziproken Gitter wir gucken! |
|
 |
Da wir erwarten, daß immer dann wenn k die Bragg-Bedingung erfüllt
(und dann kBr oder kB heißt und
niemals mit k oder kB, der Boltzmannkonstanten verwechselt wird
) - und das heißt jetzt eine BZ schneidet - mit E(kBr) oder
D(kBr)
etwas "passiert", wird dieses "etwas" jetzt in verschiedenen
Richtungen der reziproken Gitters bei verschiedenen (Beträgen der) Wellenvektoren
stattfinden müssen. |
 |
Was immer auch geschieht, wir verlieren die Kugelsymmetrie des freien Elektronengases
und erhalten dafür die Symmetrie des reziproken Gitters. |
|
 |
Und das ist ein erstes allgemeines Ergebnis, das ganz offensichtlich immer
gilt - auch für die korrekte Lösung des Problems. |
|
| |
|
Stehende Wellen als Ergebnis der Beugung |
| | |
 |
Betrachten wir den einfachen Fall einer Welle die im obigen Bild in G1
Richtung läuft und die Bragg-Bedingung erfüllt: |
|
|
|
|
 |
Offenkundig erfüllen auch die Wellenvektoren kB' die
Braggbedingung - es wird also ständig hin- und rückgebeugt |
|
 |
Für den speziellen Fall (Wellenvektor kBauf kx-Achse)
wie oben gezeigt) muß nun gelten |
|
|
Wellenvektor kB der
"hin"laufenden Welle: |
| k B = | |
G1
2 | | |
| | | |
Wellenvektor kB' der
"rück"laufenden = gebeugten Welle: |
| k 'B = | – |
G1
2 |
|
|
 |
Die Wellenfunktion für diese hin-und-hergebeugten
Elektronen ergeben sich konsequenterweise durch eine Überlagerung der Wellenfunktionen
der hin- und rücklaufenden Wellen. |
|
 |
Das muß man hier einfach so hinnehmen, aber es ist bei Elektronenwellen auch nicht anders
als bei Wasserwellen: Wenn eine Wasserwelle ans Ufer läuft und dort reflektiert ("gebeugt") wird, überlagern
sich hin- und rücklaufende Wellen. |
|
 |
Wiederum ein nur quantenmechanisch zu verstehendes Phänomen. Wenn ein "hin"laufendes
klassisches Teilchen an einer Mauer reflektiert ("gebeugt") wird, läuft
es anschließend zurück. Aber es überlagert sich nichts: Es ist entweder hin- oder rücklaufend, nicht
aber beides irgendwie gleichzeitig. |
 |
Das Ergebnis der Überlagerung zweier in entgegengesetzten Richtungen laufender
ebener Wellen ist elementar einfach und bekannt: Wir erhalten eine stehende Welle. |
|
 |
Das können wir sofort mathematisch nachvollziehen indem wir y(kBr,
r) = y0 · eikBr · r und y(– k,
r) = y0 · e– ikBr · r überlagern,
d.h. addieren oder subtrahieren (und dabei der Einfachheit
halber die Amplituden = 1 setzen). |
|
 |
Welches Vorzeichen ist das richtige? Zwar behaupten manche Leute, daß geben seeliger
denn nehmen sei, aber mathematisch sind +
und – jedoch gleichberechtigt. |
|
 |
Die Antwort ist also: Beide Vorzeichen sind richtig und
gleichberechtigt - es gibt außerhalb der Theologie keinen Grund eines zu bevorzugen. Beide
Überlagerungen liefern gleichberechtigte Lösungen für die Schrödingergleichung mit "eingeschalteter
Beugung". |
 |
Das ist natürlich ein qualitatives Argument (das auch noch ein paar Tücken
hat, wenn man genau hinschaut); aber es ist trotzdem richtig. |
|
 |
Verallgemeinern wir noch ein bißchen mehr, stellen wir fest, daß wir für
alle Elektronen mit Wellenvektoren, die auf den Rändern irgendeiner Brillouinzone
liegen, zwei mögliche Lösungen der Schrödingergleichung gibt, die wir
mit y+ und y– bezeichnen
wollen. Sie lauten: |
| |
| y+ µ exp |
æ
ç
è | i · |
G
2 | · x |
ö
÷
ø |
+ exp |
æ
ç
è | – i ·
| G
2 | · x |
ö
÷
ø |
| y– µ exp |
æ
ç
è | i · |
G
2 | ·x |
ö
÷
ø |
– exp |
æ
ç
è | – i ·
| G
2 | · x |
ö
÷
ø |
|
|
|
 |
G ist dabei der reziproke Gittervektor, der das jeweilige Stück
Brillouinzone beschreibt. |
 |
Hübsch, aber noch etwas inhaltsleer. Das ändert sich aber sofort, wenn
wir für die mit y+ und y–
beschriebenen Elektronen jetzt mal schnell die Aufenthaltswahrscheinlichkeit
ausrechnen, d.h. |y+|2 und |y–|2
bilden. Das tun wir in in einer Übungsaufgabe: |
|
|
|
 |
Wir erhalten folgendes Ergebnis |
| |
| |y+|2 µ cos2 |
æ
ç
è | G
2 |
· x | ö
÷
ø |
| |y–|2 µ sin2 |
æ
ç
è | G
2 |
· x | ö
÷
ø |
|
|
|
 |
Wir haben jetzt Maxima und Minima
der Aufenthaltswahrscheinlichkeit für die Elektronenen deren Wellenvektoren die Bragg-Bedingung erfüllen, während
für all die Elektronen, die von der Beugung nichts merken, die Aufenthaltswahrscheinlichkeit nach wie vor überall konstant ist. Für die Stellen im Gitter bei denen die Maxima/Minima
liegen gilt: |
| |
Maxima y+
Elektronen: | |
x+max = | 2n p
G | | | n = 0, 1, 2, 3,... |
| | | | | | |
Maxima y–
Elektronen: |
| x–max = |
(2n +1)p
G |
| n = 0, 1, 2, 3,... |
|
|
 |
Was bedeutet das? Im einfachsten Fall nehmen wir für den reziproken Gittervektor
in einem kubischen Gitter G = {100}. |
|
 |
Der Betrag ist dann
|G| = 2p/a; a ist die Gitterkonstante. |
|
 |
Damit erhalten wir für die maximale Aufenthaltswahrscheinlichkeit der Elektronen, die
als Welle in den Grundrichtungen der Elementarzelle laufen und die Bragg-Bedingung erfüllen: |
| |
| x+max = |
n · a | |
| n = 0, 1, 2, 3,... |
| | | |
| |
| x–max = |
n · a + a/2 |
| n = 0, 1, 2, 3,... |
|
|
|
 |
Machen wir nun aus dem Gitter den einfachstmöglichen
Kristall, indem wir auf jeden Gitterpunkt ein Atom
setzen, erhalten wir ein bemerkenswertes Ergebnis: |
 |
Die y+ Elektronen
haben ihre maximale Aufenthaltswahrscheinlichkeit am Ort der Atome, die y–
Elektronen genau dazwischen. |
|
 |
Das Ganze sieht dann so aus: |
|
|
|
|
 |
Die lila Kurve unten zeigt den tatsächlichen Verlauf
der potentiellen Energie V(x) entlang von z.B. einer <100> Richtung. |
|
 |
Die roten und blauen Kurven entsprechen den beiden Lösungen |y+|2
und |y–|2 und beschreiben damit die Aufenthaltswahrscheinlichkeit
der Elektronen. |
 |
Das hat jetzt weitreichende Konsequenzen für die Energie dieser Elektronen.
Sie "spüren" das Potential, d.h. ihre Gesamtenergie ist wohl noch konstant, aber nicht mehr rein kinetisch, im Gegensatz zu den "ebenenWellen" Elektronen,
für die sich das Potential sozusagen wegmittelt. |
|
 |
Dabei "sehen" die y– und y+ Elektronen aber verschiedene Potentiale; das wird sich dann in ihrer Gesamtenergie
bemerkbar machen. |
 |
Wenn man genauer hinschaut sieht man, dass die y+
Elektronen noch die starke Bindungskräfte des Atoms "spüren", sie sind gewissermaßen noch halb
gebunden; die y– Elektronen sind dagegen freier, sie spüren keine
oder zumindest nur stark verringerte Kräfte. |
|
 |
Anders ausgedrückt: Die effektive potentielle Energie
der beiden Elektronensorten ist anders. |
|
 |
Nochmal anders ausgedrückt: Die zum durch kB charakterisierten
Zustand gehörende Gesamtenergie ist nicht mehr eindeutig,
sondern nimmt zwei Werte an! |
 |
Da wir aber immer noch fast konstantes Potential
voraussetzen, das nur mit einer ganz kleinen periodischen Komponente moduliert ist (im Gegensatz zu obigem Bild), kann die
potentielle Energie bei uns nicht sehr verschieden sein. |
|
 |
Im realem Kristall ist die Modulation aber kräftig. Das ändert aber nicht die generelle
Beobachtung, daß bei Elektronen mit Wellenvektoren auf den Grenzen einer BZ
zwei Energieeigenwerte auftreten werden, sondern nur die Größe der Aufspaltung
und evtl. auch noch das Verhalten in der Nähe der BZ. |
|
 |
Das ist die zweite wesentliche Konsequenz
aus dem "Einschalten" eines periodischen Potentials: Die Energie für Wellenvektoren auf den Rändern
der BZ nimmt zwei Werte an; wir haben eine Energieaufspaltung. |
 |
Das sind die wesentlichen und fundamentalen Erkenntnisse, die sich qualitativ
relativ zwanglos aus dem freiem Elektronengas plus einem ganz kleinem periodischem Potential, dem Modell
des leeren Gitters, ableiten lassen. |
 |
Wir werden also in jedem Fall die Energie als Funktion des Wellenvektors an all
den Stellen, an denen die Wellenvektoren auf den Rändern (und in der Nähe) einer BZ liegen, modifizieren
müsen. Für verschiedene Richtungen im reziproken Gitter wird das an verschiedenen Stellen geschehen - die Kugelsymmetrie ist nicht mehr
vorhanden! |
|
 |
Das
kann qualitativ, in einer Art "Prinzipkurve", nur so aussehen 1): |
| |
|
 |
Das ist ein sehr wichtiges Bild. Es vereinigt die beiden wesentlichen Erkenntnisse
und führt zwangsweise auf eine dritte: |
|
 |
Aufgetragen ist die Gesamtenergie als Funktion des Wellenvektors (immer mit der k-Achse
in die jeweilige reziproke Gitterrichtung genommen). Um die jetzt bestehende Verschiedenheit
der Richtungen anzudeuten, schauen wir nach rechts in eine (100) Richtung des
reziproken Gitters, nach links in eine (111) Richtung. Die beiden kleinsten reziproken
Gittervektoren und die Ränder der Brillouinzonen sind eingezeichnet. |
|
 |
Die E(k) Funktion (die Dispersionsfunktion) des freien Elektronengases ist in Orange
eingezeichnet. Sie kennt keine Richtungsabhängigkeit; sieht also nach rechts und links gleich aus. |
|
 |
An den Schnittpunkten der E(k) Kurve mit den Rändern der
BZ müssen wir zwei Energiewerte haben. Falls wir keine pathologisch-unstetige
Funktion haben wollen, kommen wir nicht umhin, die Parabel wie gezeichnet zu modifizieren. |
 |
Damit gewinnen wir, sozusagen mit dem Bleistift, eine dritte
Erkenntnis: |
|
 |
In einer gewissen Umgebung um dem Rand einer BZ müssen wir bei der Dispersionskurve
Abweichungen von der einfachen Parabel des freien Elektronengases erwarten. |
|
 |
Das ist auch verständlich, denn die Bragg-Bedingung ist ja nicht beliebig "scharf",
sondern auch noch für Wellenvektoren eingermaßen erfüllt, die nicht
exakt auf dem Rand der BZ liegen. |
 |
Viel mehr kann man aus der Kombination "freies Elektronengas + Beugung"
nicht lernen. Wie groß die Energieaufspaltung in einer gegeben Richtung ist, wie die Dispersionkurve genau aussieht
- das ergibt nur die komplette Rechnung mit halbwegs richtigen Potentialen und einigem (mathematisch-numerischen) Aufwand. |
|
 |
Allenfalls könnten wir noch die einfachste Näherung abhandeln, das sogenannte Kronig-Penny
Modell. Wie das geht, ist aber in einem extra
Modul gezeigt. |
 |
Wir machen uns nur noch eine "dramatische" Konsequenz aus dem Vorhandensein
einer Energieaufspaltung klar: |
|
 |
In einem Realkristall müssen wir erwarten, daß es für die freien Elektronen
Energiewerte gibt, die sie grundsätzlich nicht annehmen können. Wir haben im Spektrum der möglichen Energiewerte
eine Energielücke. |
|
|
|
© H. Föll (MaWi 2 Skript)