 |
Ein Elektron des freien Elektronengases, das mit y(k,
r) = y0 · eik ·r
beschrieben wird, ist eine ebene Welle - und ebene Wellen werden an der periodischen
Kristallstruktur gebeugt, falls die Bragg-Bedingung erfüllt ist. |
|
 |
Das gilt für alle Elektronenwellen -
nicht nur für solche, die wir von außen "hineinschießen".
|
|
 |
Sobald wir also in unserem Modell des freien Elektronengases ein noch so kleines periodisches
Potential "einschalten", bewegen sich die Elektronen jetzt in einem Kristall,
und wir müssen mit (noch so kleinen) Beugungseffekten rechnen. |
 |
Man kann das Problem jetzt auf zwei Weisen angehen: |
 |
1. Wir gehen voll quantitativ vor und
lösen die Schrödingergleichung für ein periodische Potential, das die reale Situation in einem Kristall wiederspiegelt.
Das tut man am besten, indem man das periodische Potential in eine Fourierreihe
entwickelt, und damit in die Schrödingergleichung eingeht. Man hat dann immer die Option, die Terme höherer Ordnung
zu vernachlässigen, wenn man mathematisch nicht recht klar kommt. |
|
 |
Wie das aussieht kann man
sich im Link anschauen. Die Beugerei muß in den Lösungen enthalten sein, und das ist sie auch. |
|
 |
Aber der dazu nötige Aufwand ist erheblich. Für unsere Zwecke reicht es, die Lage
mehr qualitativ zu betrachten: |
 |
2. Wir betrachten also die Situation zunächst nur qualitativ
mit wenigst möglichen Änderungen relativ zum freien Elektronengas. Dazu denken wir uns zwar ein periodisches Potential
eingeschaltet, aber nur ein ganz kleines. So klein, daß wir nur mit kleinen Korrekturen
zu den Lösungen für ein konstantes Potential rechnen müssen, aber nicht mit grundsätzlich neuen Dingen. |
|
 |
Das wird dann nicht die Realität widerspiegeln, aber
vielleicht doch generelle Hinweise auf die zu erwartenden Änderungen geben. |
|
 |
Denn auch mit einem kleinen periodischen Potential werden
wir Beugung haben. Wir müssen zwar erwarten, daß die Amplituden der gebeugten Wellen dann vielleicht klein sind;
aber dafür interessieren wir uns zunächst noch nicht. Wir betrachten ausschließlich die generellen
Effekte, die durch Beugung zustande kommen. |
|
 |
Und darüber hinaus machen wir uns klar, dass all die Elektronen, die keine Beugungsbedingung
erfüllen, gar nichts tun. Sie benehmen sich nach wie
vor wie die Elektronen des freien Elektronengas Modells. |
 |
Wie es sich zeigen wird, reicht die 2. Vorgehensweise im wesentlichen aus,
um alles abzuleiten was wir hier wissen müssen. |
 |
Zur Wiederholung, und um eine ersten Eindruck zu bekommen, was uns erwartet, stellen
wir die bisherigen Erkenntnisse (im wesentlichen freies Elektrongas) den zu erwartenden
Änderungen gegenüber. |
|
 |
Warum die zu erwartenden Änderungen erwartet werden
können, wird uns in den nächsten Unterkapiteln beschäftigen. Es ist aber nicht verboten, schon jetzt mal
selbst ein bißchen darüber nachzudenken. |
|
|
|
Freies Elektronengas |
Freies Elektronengas
mit Beugung |
Potential
V(x,y,z) |
V = const = 0 |
Vx = V0 · cos (2px/a1)
Vy = V0 · cos (2py/a2)
Vz = V0 · cos (2pz/a3)
V0 ® 0 |
Wellenfunktion
y(x,y,z) |
| y = |
æ
ç
è |
1
L |
ö
÷
ø |
3/2 |
· eikr |
|
|
| y = |
æ
ç
è |
1
L |
ö
÷
ø |
3/2 |
· eikr |
|
außer für Wellenvektoren kB die gebeugt werden |
Wellenvektoren
k |
| kx = ± nx · 2p
/ L |
| ky = ± ny · 2p
/ L |
| kz = ± nz · 2p
/ L | | |
| ni = 0, ±1, ±2, ... |
|
| kx = ± nx · 2p
/ L |
| ky = ± ny · 2p
/ L |
| kz = ± nz · 2p
/ L | | |
| ni = 0, ±1, ±2, ... |
| | Energie E |
Gesamtenergie = const = Ekin |
Gesamtenergie = const = Ekin
außer für Wellenvektoren kB die gebeugt werden,
denn dann kommt etwas potentielle Energie ins Spiel |
Dispersionsfunktion
E(k) |
| E = |
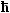 2k2 2k2
2m |
|
| E = |
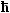 2k2 2k2
2m |
außer für Wellenvektoren kB die gebeugt werden
| Zustandsdichte
D(E) |
| D(E) = |
(2me)3/2
2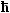 3p2 3p2 |
E1/2 |
|
| D(E) = |
(2me)3/2
2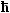 3p2 3p2 |
E1/2 |
als erste Näherung. Könnte sich aber auch kräftig ändern |
Besetzungs-
wahrscheinlichkeit
f(E,T) |
f(E, T) =
|
1
| | exp |
æ
è |
Ei – EF
kT |
ö
ø |
+ 1 |
|
f(E, T) =
|
1
| | exp |
æ
è |
Ei – EF
kT |
ö
ø |
+ 1 |
|
| gilt immer ! |
|
|
| |
 |
Im wesentlichen können wir für alle Funktionen, die k
als Variable haben, irgendwelche Änderungen erwarten, falls k die Bragg-Bedingung ungefähr
erfüllt. |
|
 |
Für alle Wellenvektoren, die das nicht tun, sollten eigentlich die Formeln des freien
Elektronengases weiter gelten |
|
 |
Obwohl es selbstverständlich ist, soll noch extra darauf hingewiesen werden, daß
die Besetzungswahrscheinlichkeit eines Energieniveaus E(k)
immer durch die Fermiverteilung gegeben ist. |
|
 |
Damit sind auch alle wesentlichen
Formeln, die wir im Zusammenhang mit der Fermiverteilung erhalten haben unverändert gültig. Man muß
nur die richtige Formel für die Zustandsdichte einsetzen, denn hier müssen wir mit Änderungen rechnen |
| |
|
© H. Föll (MaWi 2 Skript)