Kronig-Penney Modell

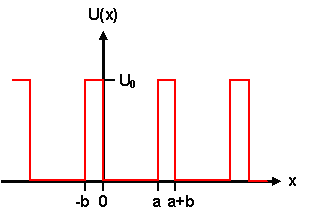
	Das Kronig-Penney Modell ist der einfachste Ansatz für ein periodisches Potential, den man machen kann. Wir behalten das konstante Potential des freien Elektronengases bei, aber ändern es periodisch. Das sieht dann so aus:
		Wie immer ist a die Gitterkonstante; die Weite b des "hohen" Potentials sowie seinen Wert U0 können wir als freie Parameter variieren.
		Insbesondere können wir U0 Þ ¥ und b Þ 0 gehen lassen, dann haben wir ein durch Delta-Funktionen unterbrochenes konstantes Potential.
	Was wir zu tun haben ist
		1. Die Schrödingergleichung in den Bereichen mit U = 0 und U = U0 prinzipiell lösen.
		2.Die erhaltenen Lösungen and den Grenzbereichen bei a, a + b, 2a, ... so zusammensetzen, daß wir für die Wellenfunktion und die erste Ableitung Stetigkeit haben. Dass diese Randbedingungen die richtigen sind, müssen wir hier einfach hinnehmen - aber was sollte man denn sonst nehmen?
	Ein im Grunde einfaches Programm, vor allem weil wir die prinzipiellen Lösung aus dem freien Elektronengasmodell schon kennen. Allerdings ist die mathematische Durchführung unerwartet anspruchsvoll, wir werden hier deshalb nur den generellen Weg beschreiben.
		Dabei müssen wir einige Behauptungen unbewiesen in den Raum stellen, und sogar einige mathematisch fragwürdige "Abkürzungen" nehmen - sonst wird es sehr lang und unübersichtlich. Aber keine Angst - das Kronig-Penney Modell "stimmt" trotzdem, das haben andere hinreichend ausführlich untersucht und gezeigt.
	Die zu lösende eindimensionale Schrödingergleichung lautet.
		–    2 2me  ·  d2y(x) dx2  + U(x) · y(x)  =  E · y(x)
	Die Lösungen sind, wie wir vom freien Elektronengas her wissen, ebene Wellen; charakterisiert durch einen Wellenvektor k. Gleichzeitig erhalten wir die Gesamtenergie E(k).
		In Formeln können wir in voller Allgemeinheit hinschreiben
		Bereiche mit U = 0 y1(k, x)  =  A · e i kx  +  B · e i kx   E1  =   2k2 2me               Bereiche mit U = U0   y2(Q, x)  =  C · e i Qx  +  D · e i Qx   E2  =  U0  –   2Q2 2me
		Um vollständig allgemein zu bleiben, müssen wir zwei verschiedene Wellenvektoren, k und Q, postulieren. Diese Wellenvektoren sind aber keine Unbekannten, wir können sie im Prinzip, wie auch schon beim freien Elektronengas, leicht ausrechnen.
	Die Randbedingungen lassen sich für z.B. die Stelle x = a leicht hinschreiben, wir haben
		y1(k , a)   =  y2(k, a)      dy 1(k, a) dx  =  dy2(k, a) dx
	Das führt sofort auf die Beziehungen
		A  +  B  =  C   +  D     ikA  –  ikB  =  QC  –  QD
	Damit haben wir zwei Gleichungen für die vier Unbekannten A, B, C und D.
		Es ist aber leicht, mehr Gleichungen zu bekommen - wir müssen nur die Randbedingungen an all den andern Potentialsprungstellen hinschreiben - das liefert uns dann sogar ¥ viele Gleichungen.
		Damit haben wir aber ein Problem - wir bekommen ein überbestimmtes Gleichungssystem, das im allgemeinen meist keine Lösungen hat. Da wir aber ein reales physikalisches System beschreiben, muss es Lösungen geben, und das bedeutet, dass von unseren ¥ vielen Gleichung genau vier unabhängig sein können und müssen.
	In anderen Worten: Die Periodizität des Potentials muss sich irgendwie auch als Periodizität in den Lösungen niederschlagen, so dass man aus der Kenntnis von y 1(k, x) auch Aussagen über y 1(k, x + a) oder y1 (k, x + 17a) etc. machen kann.
		Diese Beziehung zwischen den Lösungen regelt das sogenannte und zu Recht berühmte Bloch-Theorem .
		Für unseren Fall sagt es z.B.
		y(k, x + a)   =   y(k, x) · e i k · a

	Das kann man jetzt noch einarbeiten und erhält als weitere Gleichungen für die vier Koeffizienten der Wellenfunktionen
		A · e i ka  +  B · e i ka      =   æ è C · e i Qb  +  D · e i Qb ö ø  ·  e i k(a + b)                   æ è A · e i ka  +  B · e i ka ö ø  · ik  =   æ è C · e i Qb  +  D · e i Qb ö ø  · Q · e i k(a + b)
	OK, nun haben wir die vier notwendigen Gleichungen. Nun viel Spass beim Lösen dieses transzendenten Gleichungssystems!
		Ziemlich schwierig - mit Papier und Bleistift. Aber einen (schwierigen) Schritt kriegt man noch hin:
		Es gibt nur dann überhaupt eine Lösung, wenn die Determinante der vier Gleichungen verschwindet. Wer's schafft findet folgende, nur mit viel Mühe zu erhaltende Gleichung
		Q2  –  k2 2Qk   · sinh(Qb) · sin(ka)  +  cosh(Qb) · cos(ka) = cos[k(a + b)]
	Den meisten wird jetzt wohl immer noch kein Licht aufgehen - oder? Was haben wir denn mir dieser Gleichung gewonnen?
		Im Prinzip Energiebänder ; es ist nur nicht so ganz einfach, das der Gleichung anzusehen.
	Etwas einfacher wird es, wenn wir nur den oben schon angedeuteten Extremfall U0 Þ ¥ und b Þ 0 untersuchen, denn dann fällt so manches weg.
		Bei diesem Übergang achten wir darauf, dass das Produkt U0b konstant bleibt.
		Insbesondere gilt dann (und das zu zeigen ist auch nicht ganz einfach, aber auch nicht allzu schwer):
		Q2ba 2  =  a  =  endliche Größe     Q  >>  k       Qb << 1             cos(ka)   =   a ka   · sin(ka)  +  cos(ka)
	Das ist zwar immer noch eine transzendente Gleichung, die wir vielleicht analytisch lösen können, vielleicht auch nicht, aber eine Sache können wir relativ einfach herausfinden:
		Die linke Seite liegt für jeden Wert von ka zwischen +1 und -1 - andere Werte kann der Cosinus nicht annehmen.
		Wie ist das mit der rechten Seite? Falls sie für irgendwelche Werte von ka größer als +1 oder kleiner als -1 sein würde, heißt das ganz einfach, dass in diesem Bereich keine Lösungen existieren können.
	Das kann man nun ziemlich einfach überprüfen: Wir plotten die rechte Seite für irgendwelche Werte des Parameters P = ka und schauen mal was wir bekommen. Für a = 3p /2 z.B. die folgenden Kurven
	Was sagt uns diese Bild: Dass es für den gewählten Wert des Parameters P "verbotene" Wellenvektoren k gibt, denn für diese k-Werte kann es keine Lösungen der Schrödigergleichung geben.
		Warum a = 3p/2 ein sinnvoller Wert ist, wollen wir hier lieber nicht betrachten; auf jeden Fall aber bestimmt P offenkundig das Maximum bei ka = 0 und damit die auftretenden Bereiche ohne Lösung.
		Die "verbotenen" Bereiche liegen zwischen den grünen und blauen Linien; denn dort ist die rote (und rosa unterlegte) Funktion außerhalb des zulässigen Wertebereichs.
		Fast wichtiger ist aber die nächste Aussage: Die zu den "verbotenen" Wellenvektoren gehörende Energie ist natürlich auch verboten - wir haben "Lücken" im Energiespektrum. In anderen Worten: Wir bekommen Bänder.
		Der, zugegebenermaßen etwas ominöse Parameter a enthält die Physik - die Eigenschaften unseres "Modellpotentials". Sein numerische Wert bestimmt wo (im k- bzw. E-Bereich, die Bandlücken zu finden sind.
	Wer jetzt sehr genau hinsieht, merkt, dass wir ein bißchen geschummelt haben: Das Bloch-Theorem bezieht ich auf die Wellenfunktion yK(x), die das Gesamtproblem löst.
		Der zugehörige Wellenvektor (oder besser gesagt, die (vektorielle) Quantenzahl K ist nicht notwendigerweise identisch mit dem Wellenvektor k , der ja nur zu der Wellenfunktion gehört, die zwischen den Potentialsprüngen vorliegt!
		Falls aber die Potentialsprünge unendlich dünne Deltafunktionen sind, kann die Gesamtlösung nicht sehr verschieden sein von den Lösungen zwischen den Deltafunktionen ..... , aber jetzt hören wir auf.
	Was man hier lernen kann sind zwei Dinge:
		1. Selbst vergleichsweise einfache Probleme können in der Quantenmechanik schnell mathematisch recht anspruchsvoll werden.
		2. Aber was soll's: Es kommt immer richtig heraus; im Zweifel durch Numerik.
	Das kann man in einem JAVA- Modul selbst nachprüfen: Dort ist das Kronig-Penney Modell in voller Schönheit implementiert; als freien Parameter kann man a eingeben.

Mit Frame

4.1.2 Brillouin Konstruktion der Beugung und Brillouin Zonen

Bloch Theorem

Entwicklung des Si Banddiagramms aus den Atomzuständen

© H. Föll (MaWi 2 Skript)