|
Falls man im Modell des freien Elektronengases ein periodisches Potential einbaut,
kann man weiterkommen indem man:
- Die zugehörige Schrödingergleichung löst - sofern man das kann - und dann eine vollständige quantitative Beschreibung des Verhaltens der Elekronen erhält.
- Das Wissen um die Beugung von Elektronenwellen an periodischen Potentialen einsetzt und dann einige fundamentale
Erkenntnisse sowie eine qualitative Beschreibung der Unterschiede zum freien Elektronengas
mit konstantem Potential gewinnt
|
 |
Hier wird der zweite Weg beschritten. Dazu muß man sich zunächst klar
machen, dass die exp(ikr) Elektronenwellen des freien Elektronengases genauso an einem Gitter/Kristall
gebeugt werden wie von außen "hineingeschossene" und ebenfalls durch exp(ikr) beschriebene ebene Wellen.
|
|
 |
Für ein sich im Zustand k befindliches und dann durch
exp(ikr) beschriebenes Elektron des Kristalls gibt es jetzt zwei
Möglichkeiten:
- Es erfüllt für irgendeine Ebenenschar {hkl} des jetzt vorhandenen Gitters
die Beugungsbedingung k – k' = Ghkl, dann wird es an dieser
Ebenenschar gebeugt (d.h. reflektiert) und macht damit etwas was im Modell des freien Elektronengases nicht
vorkommt.
- Es erfüllt keine Beugungsbedingung, dann spürt es das jetzt vorhandene
Gitter überhaupt nicht und verhält sich weiterhin wie ein Elektron des freien Elektronengases.
|
 |
Die erste wichtige Schlußfolgerung ist damit, daß wir unser altes
Modell für die meisten k-Zustände weiterhin quantitativ verwenden können; nur eben nicht mehr für die Untermenge derjenigen Zustände
kB (k
"Bragg", nicht zu verwechslen mit kB, k
Boltzmann!), für die eine Beugung auftreten wird. Die Schlüsselfrage ist jetzt: |
|
 |
Wie kann man diese "speziellen" Zustände kB
aussortieren? Die Antwort gibt die Brillouin Konstruktion der Beugung: |
|
 |
Wir tragen alle Zustände k
in das reziproke Gitter des betrachteten Gitters ein; dann werden nur diejenigen kBr "gebeugt",
die auf den Mittelhalbierenden eines reziproken Gittervektors enden (man darf den Index "B"
also auch als "k Brillouin" lesen; aber hier nie als "Boltzmann"!) |
|
 |
Die Mittelhalbierenden in einem dreidimensionalen reziproken Gitter sind Flächen;
die Gesamtheit dieser Flächen bildet ein System geschachtelter "Polyeder",
die nach Größe durchnumerierbar sind. |
|
 |
Der kleinstmögliche Polyeder heißt 1. Brillouinzone
(BZ); der nächstgrößte 2. BZ usw. |
 |
Bei näherer Betrachtung der gebeugten Elektronenwellen (besonders einfach
falls kB, kB' und G kolinear sind;
dann muß kB = G/2 gelten) erkennt man, dass wir jetzt eine Überlagerung
von hin- und rücklaufenden Elektronenwellen haben, da auch die exp–(ikBr)
Welle automatisch dieselbe Bragg-Bedingung erfüllt wie die hinlaufende Welle und durch Reflektion wieder zu exp(ikBr) wird. |
|
 |
Es gibt grundsätzlich zwei Arten der linearen Überlagerung;
für den einfachen Fall der Kolinearität alle Vektoren sind das |
| |
| y+ µ exp |
æ
ç
è | i · |
G
2 | · x |
ö
÷
ø |
+ exp |
æ
ç
è | – i ·
| G
2 | · x |
ö
÷
ø |
| y– µ exp |
æ
ç
è | i · |
G
2 | ·x |
ö
÷
ø |
– exp – |
æ
ç
è | – i ·
| G
2 | · x |
ö
÷
ø |
|
|
 |
Es ergeben sich zwei stehende Wellen, mit
Maxima am Ort der Gitterpunkte /Atome oder genau dazwischen. |
|
 |
Da das periodische Potential an diesen beiden Positionen per definitionem verschieden ist,
hat der Zustand mit kBr = G/2 jetzt zwei
Energiewerte. Das gilt ganz allgemein für alle Zustände die auf den Rändern einer Brillouin Zone liegen.
|
|
 |
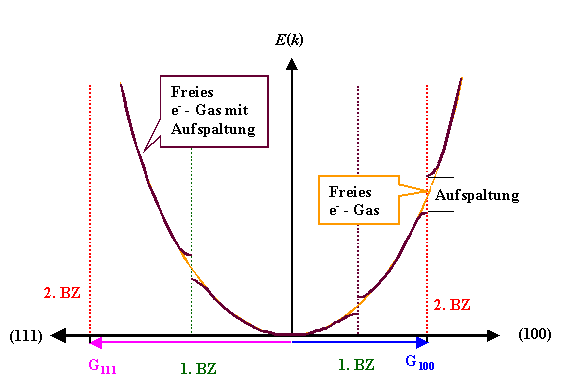
Wir erwarten also für die Dispersionskurve E(k) eine Aufspaltung
überall dort, wo die "alte" Parabel eine Brillouinzone schneidet. Das kann nur so aussehen: |
| |
|
|
 |
Dabei haben wir stillschweigend angenommen, daß auch in der Nähe einer Brillouin
Zone Abweichungen vom idealen freien Elektronengas zu erwarten sind - ziemlich wahrscheinlich, denn es gibt in der Natur
eher keine echten Singularitäten. |
 |
Wichtig ist außerdem, dass die Kugelsymmetrie des freien Elektronengases
nicht mehr vorhanden ist. Die Dispersionskurve sieht in jeder Richtung des (reziproken) Raumes anders aus - die Aufspaltung
ist bei jeweils anderen Werten, wobei jetzt aber die Symmetrie des reziproken Gitters auftauchen wird. |
|
 |
In der Grafik ist das symbolisch durch zwei verschiedene Äste dargestellt: Rechts in
die(100) Richtung, links in die (111) Richtung des reziproken Raums; d.h. senkrecht zu den (100) bzw.
(111) Ebenen des realen Raumes. |
© H. Föll (MaWi 2 Skript)