|
Auch die Elektronen(wellen) des Kristall werden gebeugt; es gilt die Bragg-Bedingung: |
|
|
 |
Die Bragg-Bedingung ist für alle Zustände (= kB;
nicht mit Boltzmannkonstant kB verwechseln!) erfüllt, die auf
den Rändern einer Brillouinzone liegen |
|
 |
Brillouinzonen sind die ineinandergeschachtelten Polyeder im reziproken Gitter, die man mit
der "Mittelhalbierenden" Konstruktion erhält. |
|
 |
Die 1. BZ ist die Wigner-Seitz EZ des reziproken
Gitters. |
| |
| |
 |
Die Untermenge der gebeugten Elektronenwellen überlagern sich zu stehenden
Wellen; es gibt grundsätzlich zwei Möglichkeiten: |
| y± = exp(ikBr) ± exp(–ikBr) | |
| y+max = |
n · a | |
| n = 0, 1, 2, 3,... |
| | | |
| |
| y–max = |
n · a + a/2 |
| n = 0, 1, 2, 3,... |
|
|
|
 |
Die Maxima der stehende Wellen liegen bei oder zwischen
den Gitterpunkten/Atomen (a = Gitterkonstante). |
|
 |
Die zugehörigen Energien müssen verschieden
sein; wir erhalten auf den Rändern der Brillouinzonen eine Energieaufspaltung der E(k)-Parabel. |
| |
| |
 |
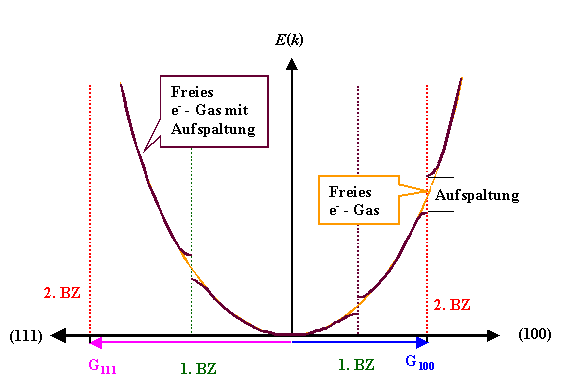
Das kann nur so aussehen: |
|
|
 |
Nur in der Nähe einer BZ ist die freie Elektronengas Dispersionskurve "verbogen";
direkt auf der BZ macht sie einen Sprung, d.h. erlaubt zwei Energiewerte für
ein k. |
|
 |
Qualitativ bleibt in dieser Betrachtung nur die Größe der Aufspaltung und der Verlauf
in der Nähe der BZ. |
© H. Föll (MaWi 2 Skript)