|
Wir basteln ein Banddiagramm |
|
|
 |
Im vorhergehenden Modul haben wir uns klargemacht, wie die E(k)-Kurven
eines realen Kristalls prinzipiell aussehen. |
|  |
Jetzt möchen wir aber wissen, wie sie wirklich aussehen. Dazu
fließen einige prinzipielle Erkenntnisse ein, die von den Festkörperphysikern mit harten Rechnungen bzw. mühsamen
Messungen erarbeitet wurden. |
|
 |
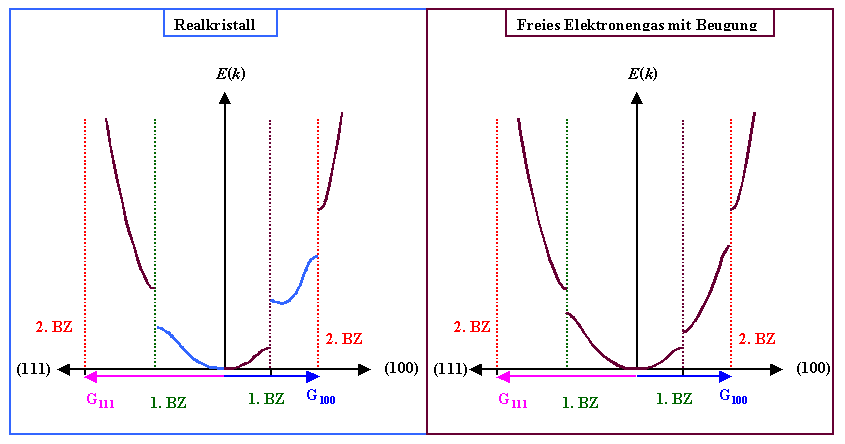
Was damit gemeint ist, sehen wir sofort, wenn wir einfach unsere "Prinzipkurve" und die reale
Kurve eines realen Kristalls einander gegenüberstellen: |
|
|
|
 |
Aha: Im Grunde brauchen wir nur zwei, "irgendwie" auch ohne lange Rechnung
verständliche Verallgemeinerungen! |
|
1. Die Größe
der Aufspaltung, d. h. die Breite der Energielücke, ist kristall- und richtungsspezifisch.
Das ist im linken Ast für die Kurve in der 1. BZ angedeutet. |
|
 |
Das heißt z. B., daß die Energielücke in der {100}-Richtung
des Si verschieden sein wird von der im Ge oder im GaAs oder ... (immer im reziproken Gitter natürlich).
|
|
 |
Es heißt auch, daß die Energielücke in der {100}-Richtung
des Siverschieden sein wird von der Energielücke in der {111}-Richtung des Si (oder der {110}-Richtung
oder der {hkl}-Richtung). Allerdings sind natürlich Kristallsymmetrien gewahrt, d. h. die geschweiften Klammern sind absichtlich gesetzt.
|
|
2. Der genaue Verlauf der E(k)-Kurve kann sich
kräftig von der einfachen Parabel des freien Elektronengases unterscheiden. Das ist im rechten Ast für die Kurve
in der 2. BZangedeutet. |
|
 |
Insbesondere muß das Minimum
oder Maximum des Energiewertes für irgendeinen Zweig, so wie im rechten
Ast gezeigt, nicht unbedingt auf dem Rand einer BZ
liegen. Das wird weitreichende Konsequenzen haben! |
 |
Unterstellen wir einfach, daß die richtigen Kurven für einen gegebenen
Kristall in allen Details bekannt sind, dann haben wir alles, was wir brauchen. Das Problem ist nur: Viele Kurven in all
diese Richtungen – es wird äußerst unübersichtlich! |
|
 |
Wir gehen deshalb zu einer stark vereinfachten
Darstellung der Energien von Kristallelektronen über: Wir betrachten nur noch, welche Energiewerte erlaubt und welche
verboten sind – und das ganz und gar unabhängig von der Richtung im reziproken Raum. Das Ergebnis ist dann ein
Banddiagramm. |
|
 |
Wie man vorgeht, ist im nächsten Bild schematisch gezeigt: |
|
|
|
 |
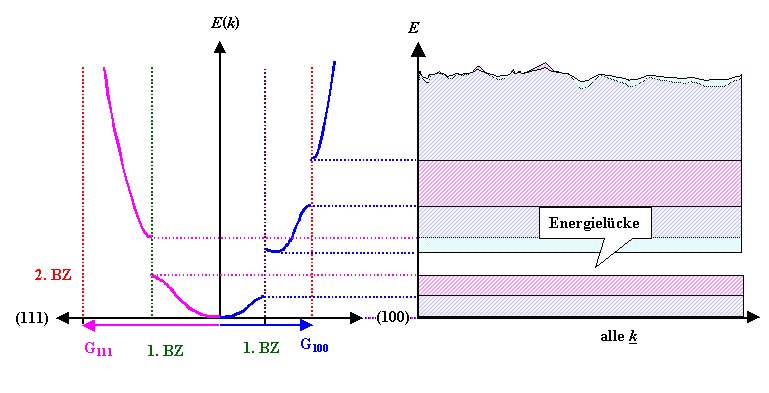
Wir projizieren einfach alle erlaubten Energiewerte
für alle Richtungen auf die Energieachse und unterscheiden nur zwischen "erlaubten"
und "nicht erlaubten" Energiebereichen. |
|
 |
Gezeigt ist zwar nur die Projektion von zwei
Ästen der Dispersionskurve, die zwei Teilbänder
ergeben; wir können die Vorgehensweise aber natürlich "leicht" auf alle
Äste ausdehnen. Die dadurch erhaltenen "Bänder" aller
möglichen Energiewerte geben dem Diagramm den Namen: Es heißt Banddiagramm. |
|
 |
Die Energielücke ist prominent zu sehen, wir nennen sie ab jetzt auch Bandlücke
(bzw. im Laborslang auch "Bandgap"). |
 |
Es gibt zwar nach wir vor zu jeder beliebigen herausgegriffen Energie (mehrere)
bestimmte k-Werte, aber die interessieren uns nicht mehr im Detail; wir merken uns lediglich die Tatsache
an sich, daß es sie gibt. |
|
 |
Da wir das Banddiagramm als stark vereinfachte Darstellung der Gesamtheit der E(k
)-Kurven betrachten, steht an der x-Achse keine Achsenbezeichnung, da sie keinerlei Information mehr enthält.
(Das in der Zeichnung oben angegebene "alle k" ist rein symbolisch zu verstehen!) |
|
 |
Wir können sogar einen Schritt weitergehen und z. B. auch " x"
oder "z" oder <110> an die Abszisse schreiben, d. h. eine Darstellung der erlaubten
Energien im Ortsraum wählen – das Banddiagramm sieht weiterhin genauso aus.
(Davon werden wir später bei der Beschreibung einer Diode oder anderer Bauelemente viel Gebrauch machen!) |
|
 |
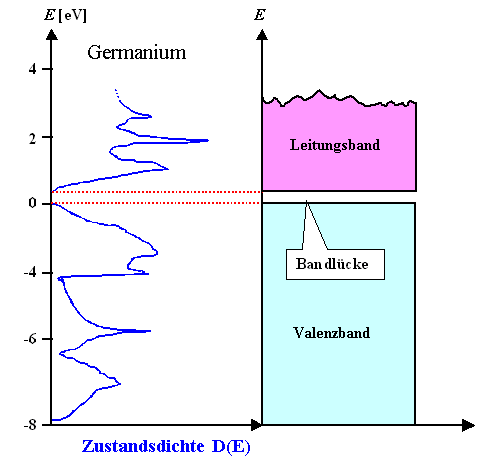
Wir können es leicht wieder etwas komplizierter (aber damit auch aussagekräftiger)
machen und die Abszisse für die Zustandsdichte
D(E) nutzen. Auf die Details gehen wir hier und jetzt nicht weiter ein (sie folgen schon ein klein
wenig weiter unten), sondern nehmen einfach nur schon mal das Ergebnis an einem konkreten Beispiel (Germanium) zur Kenntnis: |
| |
|
|
 |
Aufpassen: Wir haben es bei der Zustandsdichte D(E) zwar mit einer Funktion
"D von E" zu tun, in der hiesigen Darstellung sind aber die Achsen absichtlich vertauscht –
die Funktionswerte D sind auf der Abszisse, die Werte der Variablen E
, von der sie abhängen, auf der Ordinate zu finden. |
|
 |
Auf diese Art der Darstellung von Funktionen, die von der Energe abhängen, werden wir
im Zusammenhang mit dem Banddiagramm übrigens noch öfters stoßen; wir tun gut daran, uns an die zugehörige
Denkweise zu gewöhnen, denn wir werden sie später selber verwenden – in einer sehr wichtigen Übungsaufgabe. |
 |
In Form der Zustandsdichte "überlebt" immerhin ein Teil der Eigenschaften der
E(k)-Kurven die Vereinfachung der Bandstruktur zum Banddiagramm. Aber auch die Details der Zustandsdichte
interessieren uns nur selten; wir merken uns lediglich die Tatsache an sich, daß es sie gibt. |
|
 |
Ein Detail der Zustandsdichte ist allerdings sehr wichtig: In der Bandlücke des idealen
Kristalls ist die Zustandsdichte per definitionem = 0. |
|
 |
Das läßt sich aber durch gezielte Abweichungen von der Idealität gezielt
ändern, wie wir später noch sehen werden!
|
 |
Wir fangen, um Zustandsdichten zu verstehen,
nochmal ganz von vorne an: |
|
 |
Wir haben ein Atom, z. B. ein Si-Atom. Wir lösen die Schrödingergleichung für seine 14 Elektronen und bekommen ¥
viele Lösungen oder Zustände
yn,l,m(x,y,z), die nach den Quantenzahlen
n, l, m sortiert werden, außerdem eine Energie En,l,m
für jeden Zustand. |
|
 |
Wir wissen, daß auf jedem Zustand zwei und nur zwei Elektronen sitzen können:
Eines mit "Spin rauf" (bzw. vierte Quantenzahl s = +½) und eines mit "Spin runter"
(bzw. s = –½). |
|
 |
Bei näherer Betrachtung der Lösung stellen wir fest, daß verschiedene
Zustände dieselbe Energie haben können. Auf einem Energienievau haben dann mehr als zwei Elektronen Platz; wir
nennen das betreffende Energieniveau dann so-und-so-viel-fach entartet. |
 |
In einem schematischen Potentialtopfbild stellen
wir das so dar: |
| | |
| |
|
 |
Gezeigt sind die Energieniveaus der Elektronen des Atomsin
einem Potentialtopf. Die Elektronen füllen "von unten her", d. h. von den tiefsten Energien her, die verfügbaren
Zustände oder Plätze auf. |
| | |
 |
Ein Energieniveau wird häufig entartet sein, es gibt
dann doppelt so viel Plätze (Spin rauf / runter) wie der jeweilige Entartungsgrad angibt. |
| | |
 |
Die Wellenfunktionen
der Zustände habe eine typische Gestalt; sie codieren hier die Aufenthaltswahrscheinlichkeit
des Elektrons. Im Schemabild sind zwei Beispiele für Wellenfunktionen gezeigt |
| | |
 |
Auf irgendeinem Energieniveau ist dann das letzte Elektron untergebracht – im Schemabild
sind das 2 durch grüne Pfeile symbolisierte Elektronen. Bei Si wäre das das 3p2-Niveau,
d. h, das Energienieveau das zu den Quantenzahlen
n = 3, l = 1 = s gehört, und auf dem 2 Elektronen sitzen. Diese
beiden Elektronen sind in der Abbildungs links (Suchbild!) schematisch durch die grünen Pfeile mit Spin rauf / runter
dargestellt. |
| |
|
 |
Jetzt bilden wir einen Silizium-Kristall.
Dazu nehmen wir viele Atompotentialtöpfe und überlagern sie im richtigen Bindungsabstand graphisch und rein qualititativ.
Wir bekommen das schon oft verwendete schematische Bild: |
|  |
Die "oberen" Energieniveaus spalten in zahlreiche Einzelniveaus
auf, damit die 1024 oder so Elektronen des Kristalls genügend Zustände finden – nur mit
Entartung eines (atomaren) Energieniveaus ist das nicht zu schaffen. |
| |
|
|
 |
Außerdem ist die Energie der Elektronen in der entstehenden Bandstruktur
etwas tiefer als im Einzelatom – denn sonst gäbe es keinen Grund, warum die Atome überhaupt Bindungen eingehen
sollten. |
|
 |
Im Gegenteil: Es gibt einen Grund, der gegen eine Bindung spricht, denn wir wissen
jetzt ja, daß auch die Entropie eine Rolle spielt, und da aneinander gebundene Atome "ordentlichder" sind
als ungebundene, sind letztere bevorzugt, weil sie die Entropie maximieren (2. Hauptsatz der Thermodynamik). Weil aber letzten
Endes das Minimum der freien Energie G = U – TS entscheidend ist, gibt es doch eine Bildung
– die Energieabsenkung muß nur groß genug sein. |
 |
Im rechten Teil des obigen Bildes ist gezeigt, wie das wirklich geht. |
|
 |
Die beiden "letzten" besetzten Niveaus beim Si-Atom sind 3s2
und 3p2. Bringt man die Atome von Abstand r = ¥
auf kleinere Abstände, beginnen sie sich so um r = 1 nm zu "spüren". Mit kleiner
werdendem Abstand spalten die beiden Einzelniveaus auf in jeweils zwei durch eine Energielücke
, d. h. zustandsfreie Zone getrennte "Bänder". |
|  |
Beim tatsächlichen Bindungsabstand (= Energieminimum unter Berücksichtigung
der hier nicht gezeigten abstoßende Kräfte) entstehen das Valenzband und
das Leitungsband, getrennt durch eine Energielücke von 1,1 eV), jeweils
aus einer Mischung von 3s- und 3p-Zuständen (den zuvor mal kurz erwähnten sp3-Hybridorbitalen ). |
|  |
Die Zustände im Valenzband liegen energetisch tiefer als im Atom. Bindung
und Kristallbildung bringt also tatsächlich eine beträchtliche Energieabsenkung für die 3p-Elektronen
des Einzelatoms, und selbst die 3s-Elektronen können sich energetisch noch etwas "verbessern". |
 |
Wie kommen wir jetzt auf die Zustandsdichte
in den Bändern? Erstmal durch Nachdenken und Rechnen! |
|
|
| Zur Berechnung der Zustandsdichte |
| |
 |
Was unter dieser Überschrift steht, ist nur für
das Verständnis wichtig. Gläubige, die das Ergebnis ohne weiteres akzeptieren, können das alles überschlagen.
Wissen muß man die Details jedenfalls nicht. |
| |
 |
Was wir grundsätzlich zu tun hätten, ist klar: Wir schreiben das in
drei Dimensionen periodische Potential der Elektronen hin (also eine passende Formel für die oben gezeigten Töpfe),
setzen die Formel in die Schrödingergleichung
ein, und lösen sie dann. |
|
 |
Das geht – mit diversen Tricks und Näherungen. Wer mal sehen will,
wie man anfängt, betätigt die Links: Noch
relativ einfach – Mit Fouriertransformationen. |
 |
Wir haben das übrigens im Ansatz auch schon mal gemacht: In Übung 2.3.1, die wir aber "damals" noch nicht so ernst genommen
haben. |
|
 |
Was haben wir in dieser Übung gemacht? Das schauen wir uns jetzt nur der Spur nach an;
es wird uns aber sehr deutlich machen, wie man zu den Zustandsdichten in den Bändern kommt. |
 |
1. Schritt: Wir haben statt einem periodischen
Potential in einer Näherung
(noch vollständig unklarer Güte), erstmal ein konstantes
Potential genommen, und damit erstmal nur eine eindimensionale Schrödingergleichung aufgestellt. |
 |
2. Schritt: Löse die Schrödingergleichung. Die Lösungen
waren einigermaßen einfach zu erhalten. Wir bekamen (erweitert auf dann drei Dimensionen) die Wellenfunktionen oder
Zustände: |
|
|
| y(r) | = |
æ
ç
è |
1
L |
ö
÷
ø | 3/2 |
· exp | (i · k · r) |
| kx = ± |
nx · 2p
L |
| ky = ± |
ny · 2p
L |
| kz = ± |
n z · 2p
L |
| E | = |
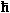 2 · kx2 2 · kx2
2me |
|
|
|
 |
Die Quantenzahlen sind die nx,y,z die auf den Wertebereich nx,y,z=0,
±1, ±2, ...ny beschränkt sind. Wir haben also formal folgende Zustände und Energien
- ynx, ny, nz(
r)=yk (r).
- E nx, ny, nz=Ek
wobei wir als Index für die Quantenzahlen der einfacheren Schreibweise wegen auch gleich den hier diskreten Wellenvektor k als eine Art vektorieller Quantenzahl schreiben.
|
 |
3. Schritt: Interpretation der Lösungen als ebene
Wellen mit Impuls 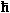 k und rein kinetischer Energie E= k und rein kinetischer Energie E=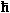 2 ·
kx 2 / 2me. Das interessiert uns hier aber nicht mehr so sehr. 2 ·
kx 2 / 2me. Das interessiert uns hier aber nicht mehr so sehr. |
 |
4. Schritt: Berechnung der Energieniveaus und des Entartungsgrades. |
|
 |
Das ist der Punkt, an dem wir hier besonders interessiert sind. Die Vorgehensweise ist einfach:
Wir fangen bei den kleinstmöglichen k-Werten an und berechnen jeweils die Energie aus obiger Formel.
Dabei fällt uns sofort auf, dass praktisch immer Entartung vorliegt, da ein-und
derselbe Zahlenwert für k x2 und damit E sich aus verschiedenen k's
ergibt: |
| |
| Quantenzustand |
Energie
(× Konstante ) |
Zustände |
Zahl der e–
pro E
| | nx |
ny |
nz |
| 0 | 0 | 0 |
0 |
|
1 | 2 |
±1
0
0 | 0
±1
0 |
0
0
±1 |
1 |
2
2
2 |
6 |
12 | ±1
±1
0
| ±1
0
±1 |
0
±1
±1 |
2 |
4
4
4 |
12 |
24 | | ±1 |
±1 | ±1 |
3 | |
8 | 16 |
±2
0
0 | 0
±2
0 |
0
0
±2 |
4 |
2
2
2 |
6 |
12 |
| Weiter ohne Details | | 2
| 1 | 0 |
5 | |
| 48 |
| 2 | 1 | 1 |
6 | |
| ? |
| 2 | 2 | 0 |
8 | |
| ? |
| 2 | 2 | 1 |
9 | |
|
? |
| 3 | 0 | 0 |
| |
und so wie weiter? |
|
|
 |
Zeichnet man das schematisch auf, erhält man das folgende Energie und Besetzungsschema: |
| |
|
 |
Damit haben wir alles was wir brauchen: Wir halten fest. |
| |
- Schon ein extrem einfaches Potential gibt uns ein "kompliziertes" Energieschema. Wir haben alle Energien von
"0" bis "10" – außer der Energie "7". Warum das so ist, ist
klar: "7" kann nicht als Summe dreier Quadratzahlen dargestellt werden.
- Der Entartungsgrad und damit die Zahl der Plätze N pro E-Niveau ist von E-Niveau
zu E -Niveau recht verschieden - wir haben die Sequenz 1 - 6 - 12 - 8 - 6 - ....
- Auf Anhieb ist nicht so recht klar wie's weitergeht - es ist kein Bildungsgesetz für den Entartungsgrad erkennbar.
|
|
 |
Der dritte Punkt ist aber etwas irreführend. Aus der Abzählung wie in der Tabelle
vorgenommen, läßt sich zwar in der Tat kein Bildungsgesetz für Energien und Entartungsgrad erkennen, aber
wenn man ein bißchen genauer hinschaut findet man eine einfache Formel für die Zustandsdichte D(E)=dN/dE
, die für nicht zu kleine Energien eine gute Näherung darstellt. |
| |
| D( E) = |
1
Vkrist |
· |
N(E + DE) – N(E)
DE | = |
1
Vkrist | · |
dN( E)
dE | = |
(2 · me)3/2
2 · p2 · 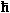 3 3 |
· E 1/2 |
|
|
 |
In Worten: Im Bereich E und E + DE gibt es D(E) · DE
Zustände
und damit genau doppelt so viel Plätze pro cm3
für Elektronen |
|
 |
Mehr wollten wir eigentlich gar nicht wissen. |
| |
 |
Wie gut ist denn die Näherung mit konstantem Potential oder, wie man das
allgemein nennt, die Näherung des "freien Elektronengases"? |
|
 |
Erstaunlich gut! Aber notgedrungen doch noch weit weg von der Realität.
Eine reale Zustandsdichte sieht zum Beispiel so aus (wir kennen sie von oben): |
| |
|
 |
Woher hat man diese Kurven? In der Regel sind sie gemessen.
Wie, das lassen wir mal dahingestellt. |
|
 |
Heutzutage kann man Zustadsdichten von nicht zu komplexen Kristallen aber auch hinreichend
genau rechnen – allerdings aber nicht mehr "von Hand". |
|
 |
Was immer sich ergibt: das Prinzip ist dasselbe wie beim freien Elektronengas. Dass nicht
immer alles in einfachen Formeln ausgedrückt werden kann, ist halt so. |
 |
Das einzige, was man sich merken muß, ist dies: Die Zustandsdichte (in Form
einer Kurve) eines (Halbleiter) Materials ist letztlich ein "Materialparameter".
Hat man diesen Parameter einmal gemessen oder gerechnet, hat man ihn für alle Zeiten. |
|
Zu diesem Abschnitt gibt es derzeit weder eine Übungsaufgabe
noch schnelle Fragen. |
© H. Föll (MaWi für ET&IT - Script)