8.2.2 Brillouin-Zonen und stehende Elektronenwellen

	Das reziproke Gitter
	Wir haben mit der vektoriellen Formulierung der Bragg-Bedingung einen außerordentlich weitreichenden Schritt gemacht, denn wir haben Netzebenenscharen {hkl} durch Vektoren Ghkl repräsentiert. Was folgt daraus für die Vektoren Ghkl?
		Wir wissen, daß Ghkl kein "normaler" Vektor ist, weil er (genau wie ein Wellenvektor) die Einheit m–1 hat. Alle Vektoren Ghkl liegen also in einem eigenen Raum.
		Nehmen wir nun alle möglichen Netzebenen {hkl} eines gegebenen Gitters, konstruieren die jeweiligen Vektoren G hkl und tragen all diese Vektoren in ihrem eigenen Raum von dem gemeinsamen Ursprung an auf, so definieren die Endpunkte aller dieser Vektoren ebenfalls ein Gitter .
		Dieses Gitter nennen wir das reziproke Gitter, die Vektoren G heißen reziproke Gittervektoren .
	Das reziproke Gitter läßt sich in eineindeutiger Weise aus den Raumgitter konstruieren (d. h. die Umkehrung gilt auch). Das reziproke Gitter ist damit vollkommen äquivalent zum Raumgitter, d. h. es enthält exakt dieselbe Information wie das Raumgitter.
		Es ist aber für alle Phänome, die sich mit Wellen in Kristallen befassen, ungleich wichtiger als das Raumgitter, da sich die Mathematik darin sehr viel einfacher gestaltet (oder sie sich überhaupt nur im reziproken Gitter durchziehen läßt).
		Das reziproke Gitter läßt sich anschaulich rein geometrisch anhand der definierenden Eigenschaften der reziproken Gittervektoren konstruieren; dies ist im folgenden zweidimensionalen Beispiel gezeigt und wird kurz daran erläutert.
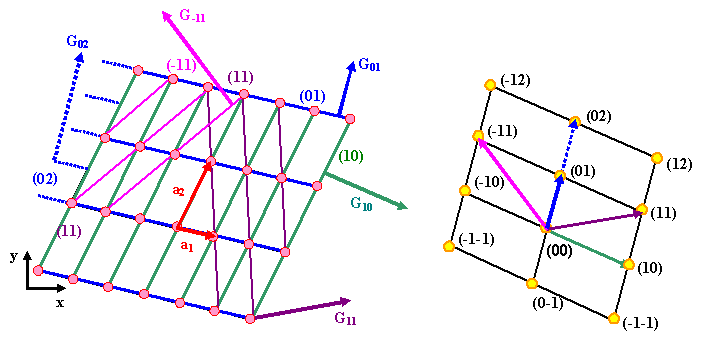		Raumgitter Reziprokes Gitter
		Links ist das (zweidimensionale) Raumgitter gemalt – das sind die rosafarbenen Punkte. Weiterhin sind einige "Ebenen"scharen eingezeichnet (was hier natürlich Scharen paralleler Geraden sind); jede Schar hat eine eigene Farbe.
		Auf einer Ebene der Ebenenschar, welche hier durch ihre Miller-Indizes (hk) gegeben ist, wird der reziproke Gittervektor konstruiert und eingezeichnet. Länge und Richtung dieses ersten reziproken Gittervektors können wir (noch) willkürlich wählen (damit legen wir die reziproke Skala in m–1 fest), die restlichen müssen sich an die dann definierte Skala halten.
		Wir wiederholen die Prozedur auf den restlichen Ebenen (wobei wir darauf achten, ein rechtshändiges System zu konstruieren); damit bekommen wir einen Satz von Vektoren, den wir allgemein mit Gij bezeichnen. Alle Gij zeichnen wir jetzt von einem gemeinsamen Ursprung aus ein und erhalten damit das reziproke Gitter – siehe das Bild rechts.
	Die formale Definition sowie die Behandlung weiterer mathematischer Eigenschaften des reziproken Gitters schenken wir uns an dieser Stelle, da wir sie im Rahmen dieser Vorlesung nicht benötigen.

	Die Brillouin-Konstruktion der Beugung
	Wir kehren jetzt gedanklich zu unseren Kristallelektronen zurück: Wir hatten uns einerseits klargemacht, daß man deren Zustände quantenmechanisch mit (modifizierten) ebenen Wellen beschreiben kann, aber andererseits haben wir gelernt, daß Wellen, die durch das Kristallgitter laufen, an demselben gebeugt werden – falls ihr Wellenvektor die Bragg-Bedingung erfüllt.
		Genau für diese Wellenvektoren interessieren wir uns besonders, denn nur die zugehörigen Elektronen werden in ihrem Verhalten von dem freier Teilchen abweichen.
		Alle anderen Elektronen merken ja nichts von den Atomen, denn ihre Wellen werden nicht gebeugt – d. h. sie unterliegen keiner Wechselwirkung und verhalten sich wie freie Teilchen.
		Die betroffenen Wellenvektoren nennen wir mal kBr. Schön wäre eine simple Formel (oder eine anschauliche Konstruktion), mit der man die k Br für ein gegebenes Gitter aus der Menge aller möglichen Wellenvektoren k heraussieben könnte.
	Moment mal: Was genau ist eigentlich die "Menge aller möglichen Wellenvektoren"? Wo finden wir die?
		Antwort: Sie gehören zum reziproken Raum! Von dem kennen wir zwar bislang nur die paar Vektoren, die das reziproke Gitter aufspannen, aber zwischen diesen Gitterpunkten ist noch viel Platz – so wie im "normalen" Raum viel Platz zwischen den "normalen" Gitterpunkten ist.
		Im Prinzip können wir alle Wellenvektoren, die wir als Lösung der Schrödingergleichung für das freie Elektronengas erhalten, beim reziproken Gitter mit einzeichnen; damit wählen wir das reziproke Gitter als Darstellungsraum für die nun folgende Brillouin-Konstruktion der Beugung.
		Das ist ja auch insofern naheliegend, weil die vektorielle Form der Bragg-Bedingung, k – k' = Ghkl , unmittelbar auf die Vektoren des reziproken Gitters führt. Außerdem haben wir noch die Bedingung | k | = | k' |.
	Was sagen uns diese Gleichungen über die gesuchten Vektoren kBr?
		Das ist einfach: Wir interpretieren die erste Gleichung um als Addition zweier Vektoren, indem wir sie als k + (–k') = Ghkl schreiben. Die zweite Gleichung wiederum sagt, daß die beiden Vektoren, die wir addieren, gleich lang sind.
		Anschaulich bedeutet dies, daß wir (entsprechend der ersten Gleichung) vom Ursprung des reziproken Raumes starten und nach zwei Schritten bei einem Punkt des reziproken Gitters landen, wobei diese beiden Schritte (entsprechend der zweiten Gleichung) gleich groß sind.
		Klar ist: Alle als erster Schritt dienende Wellenvektoren k, mit denen das klappt, sind die gesuchten k Br. Aber welche sind das?
	Die Lösung besteht darin, daß wir auf jede Strecke, die vom Ursprung zu einem reziproken Gitterpunkt führt, die Mittelhalbierende zeichnen. Alle Wellenvektoren, die auf einer dieser Mittelhalbierenden enden, erfüllen die Bragg-Bedingung!
		Das schauen wir uns in einer simplen Graphik eines zweidimensionalen Gitters exemplarisch an:
		Direkt sichtbar ist, daß jeder k-Vektor, der auf einer der rosafarbenen Mittelhalbierenden endet, einen gleich langen Wellenvektor k' produzieren "darf", der die Bragg-Bedingung k – k' = G erfüllen kann. Eingezeichnet sind der Einfachheit halber die –k' -Vektoren.
		Im dreidimensionalen Fall funktioniert das auch, bloß haben wir dann Flächen als Mittelhalbierende.
		Diese Flächen werden sich schneiden und ein System von ineinandergeschachtelten Polyedern bilden, je nachdem, wie weit entfernt vom Ursprung der jeweils betrachtete reziproke Gitterpunkt liegt.

	Die Brillouin-Zonen
	Wir führen jetzt einen besonderen Namen für das kleinstmögliche dieser Polyeder (welches die Elementarzelle des reziproken Gitters ist) ein: Wir nennen sie die erste Brillouin-Zone, abgekürzt 1. BZ.
		Nach der 1. BZ kommt die 2. BZ, danach die 3. BZ und so weiter – wir betrachten einfach die sich ergebende Abfolge von ineinandergeschachtelten Polyedern, die sich automatisch ergibt, wenn man das Mittelhalbierenden-Rezept konsequent fortsetzt.
		Leicht gesagt, nicht ganz so leicht dreidimensional durchgeführt. Aber schon früh hat man Doktoranden gequält und perspektivische Zeichnungen erstellen lassen – in diesem Fall war es 1965 Herr Lück (und damals gab es noch keine Computergraphik!):
		Es ist schon ganz erstaunlich, wie man von einem einfachen Würfel durch sukzessive Anwendung eines einfachen Rezepts zu recht komplizierten Edern kommt. Aber das soll uns nicht stören; niemand muß diese Strukturen auswendig können.
	Wir sehen jedoch eine erste Konsequenz für die Darstellung von Kristall-Elektronen-Wellenfunktionen im k-Raum:
		Die beim freien Elektronengas noch vorhandene Kugelsymmetrie geht verloren, dafür bekommen wir Symmetrieelemente des Gitters: Beim freien Elektronengas ist es völlig egal, in welche Richtung im reziproken Raum der k-Vektor zeigt, Funktionen wie E(k) oder D(k) sehen immer gleich aus. Im Kristall aber schneidet ein variierendes k eine Brillouin-Zone nach der anderen, und wo diese Schnittpunkte liegen, hängt von der Richtung von k ab – und damit davon, in welche Richtung im reziproken Gitter wir gucken!
		Da wir erwarten dürfen, daß immer dann, wenn k eine BZ schneidet – d. h. die Bragg-Bedingung erfüllt und dann k Br heißt –, mit der zugehörigen Energie E(kBr ) oder der Zustandsdichte D(kBr) etwas "passiert", wird dieses "etwas" also in verschiedenen Richtungen der reziproken Gitters bei verschiedenen (Beträgen der) Wellenvektoren stattfinden.

	Stehende Wellen als Ergebnis der Beugung
	Betrachten wir den einfachen Fall einer Welle, die im obigen Bild in G1-Richtung läuft und die Bragg-Bedingung erfüllt:
		Offenkundig erfüllen auch die Wellenvektoren k' die Bragg-Bedingung – es wird also ständig hin- und rückgebeugt. Für den speziellen Fall (Wellenvektor kBr wie oben gezeigt auf der kx -Achse) gilt also
		Wellenvektor kBr der "hin"laufenden Welle:   kBr  =    G1 2           Wellenvektor k' Br der "rück"laufenden = gebeugten Welle:   k'Br =  –  G1 2
	Die Wellenfunktion für diese hin und her gebeugten Elektronen ergeben sich konsequenterweise durch eine Überlagerung der Wellenfunktionen der hin- und rücklaufenden Wellen.
		Das muß man hier einfach so hinnehmen, aber es ist bei Elektronenwellen auch nicht anders als bei Wasserwellen: Wenn eine Wasserwelle ans Ufer läuft und dort reflektiert ("gebeugt") wird, überlagern sich hin- und rücklaufende Wellen.
		Das Ergebnis der Überlagerung zweier in entgegengesetzten Richtungen laufender ebener Wellen gleicher Wellenlänge ist elementar einfach und bekannt: Wir erhalten eine stehende Welle.
		Das können wir sofort mathematisch nachvollziehen, indem wir y(kBr, r ) = y0 · eik Br · r und y (–kBr, r) = y 0 · e– ikBr · r überlagern , d. h. addieren oder subtrahieren (und dabei der Einfachheit halber die Amplituden = 1 setzen).
	Welches Vorzeichen ist bei der Überlagerung das richtige? Zwar behaupten manche Leute, daß Geben seliger denn Nehmen sei, aber mathematisch sind + und – jedoch gleichberechtigt.
		Die Antwort ist also: Beide Vorzeichen sind richtig und gleichberechtigt, denn beide Überlagerungen liefern gleichberechtigte Lösungen für die Schrödingergleichung "mit eingeschalteter Beugung".
		Verallgemeinern wir noch ein bißchen mehr, stellen wir fest, daß es für alle Elektronen mit Wellenvektoren, die auf den Rändern irgendeiner Brillouinzone liegen, zwei mögliche Lösungen der Schrödingergleichung gibt, die wir mit y + und y– bezeichnen wollen. Sie lauten:
		y+  µ   exp æ ç è i · G 2 · x ö ÷ ø  +  exp æ ç è – i · G 2 · x ö ÷ ø y–  µ   exp æ ç è i · G 2 ·x ö ÷ ø  –  exp æ ç è – i · G 2 · x ö ÷ ø
		G ist dabei der jeweilige reziproke Gittervektor, der auf das betrachtete Stück Brillouinzone führt.
	Hübsch, aber noch etwas inhaltsleer. Das ändert sich aber sofort, wenn wir für die mittels y+ und y– beschriebenen Elektronen jetzt mal schnell die Aufenthaltswahrscheinlichkeit ausrechnen, d. h. | y+|2 und |y–|2 bilden.
		Wir erhalten folgendes Ergebnis:
		|y +|2  µ    cos2 æ ç è G 2  · x ö ÷ ø |y– |2  µ   sin2 æ ç è G 2  · x ö ÷ ø
		Wir haben jetzt Maxima und Minima der Aufenthaltswahrscheinlichkeit für die Elektronen, deren Wellenvektoren die Bragg-Bedingung erfüllen (während für all die Elektronen, die von der Beugung nichts merken, die Aufenthaltswahrscheinlichkeit nach wie vor überall konstant ist).
		Für die Stellen im Gitter, bei denen die Maxima/Minima liegen, gilt:
		Maxima der y+-Elektronen:      x+max  =   2n p G         n = 0, 1, 2, 3, ...             Maxima der y–-Elektronen:      x–max  =   (2n +1)p G       n = 0, 1, 2, 3, ...
	Was bedeutet das?
		Zur Veranschaulichung betrachten wir einen besonders einfachen Fall und nehmen für G den ersten reziproken Gittervektor in einem kubischen Gitter, G100 .
		Dessen Betrag ist |G| = 2p/a; a ist die Gitterkonstante.
		Damit erhalten wir für die maximale Aufenthaltswahrscheinlichkeit der Elektronen, die als Welle in den Grundrichtungen der Elementarzelle laufen und die Bragg-Bedingung erfüllen:
		x+max  =   n · a         n = 0, 1, 2, 3, ...           x–max  =   n · a  +  a/2   n = 0, 1, 2, 3, ...
		Machen wir nun aus dem Gitter den einfachstmöglichen Kristall , indem wir auf jeden Gitterpunkt ein Atom setzen, erhalten wir ein bemerkenswertes Ergebnis:
	Die y+-Elektronen haben ihre maximale Aufenthaltswahrscheinlichkeit am Ort der Atome, die y– -Elektronen genau dazwischen. Graphisch sieht das so aus:
		Die Atome sind in Grün eingezeichnet. Die lilafarbene Kurve unten zeigt den lokalen Verlauf der potentiellen Energie V(x) entlang einer <100>-Richtung.
		Die roten und blauen Kurven entsprechen den beiden Lösungen | y+|2 und |y –|2 und beschreiben damit die Aufenthaltswahrscheinlichkeit der Elektronen.
	Das hat jetzt weitreichende Konsequenzen für die Gesamtenergie dieser Elektronen. Sie "spüren" das atomare Potential, d. h. ihre Gesamtenergie ist wohl noch konstant, aber nicht mehr rein kinetisch – im Gegensatz zum Fall der Laufende-Wellen-Elektronen, für die sich das atomare Potential sozusagen wegmittelt.
		Dabei "erleben" die y–- und y+ -Elektronen aber verschiedene Potentiale – und das wird sich dann in ihrer Gesamtenergie bemerkbar machen, weil sich die effektive potentielle Energie der beiden Elektronensorten unterscheidet.
		Die y+-Elektronen befinden sich gewissermaßen "im Potentialtrichter" und spüren daher noch stark die Bindungskräfte der Atome; dadurch ist ihre Gesamtenergie leicht abgesenkt.
		Die y– -Elektronen sind dagegen freier, sie spüren keine oder zumindest nur stark verringerte Bindungskräfte; ihre Gesamtenergie ist daher leicht erhöht.
		Deshalb ist die zum durch kBr charakterisierten Zustand gehörende Gesamtenergie nicht mehr eindeutig, sondern nimmt zwei Werte an!
	Fazit: Die Energie für Wellenvektoren auf den Rändern der BZ nimmt zwei Werte an; wir haben eine Energieaufspaltung.
		Wir werden also in jedem Fall die Energie als Funktion des Wellenvektors an all den Stellen, an denen die Wellenvektoren auf den Rändern (und in der Nähe) einer BZ liegen, modifizieren müsen.
		Für verschiedene Richtungen im reziproken Gitter wird das an verschiedenen Stellen geschehen.
		Das kann qualitativ, in einer Art "Prinzipkurve", nur so aussehen (nach rechts ist eine (100)-Richtung des reziproken Gitters, nach links eine (111)-Richtung gezeigt):
		Die orangefarbene Parabel ist die Energie der quasi-freien Elektronen, denn für diese gilt (wie wir uns im vorigen Modul in Erinnerung gerufen haben) E(k) ~ k 2.
		An den Schnittpunkten der E(k)-Kurve mit den Rändern der BZ haben wir zwei Energiewerte. Falls wir keine pathologisch-unstetige Funktion erhalten wollen, kommen wir nicht umhin, die Parabel wie gezeichnet zu modifizieren.
	Fazit: In einer gewissen Umgebung am Rand einer BZ weichen die E(k)-Kurven von der einfachen Parabel des freien Elektronengases ab, denn für die quasi-freien Kristallelektronen kann es Energiewerte geben, die sie unter keinen Umständen annehmen können – wir haben dann im Spektrum der möglichen Energiewerte eine Energielücke.
		An dieser Stelle sollte uns dämmern, was es in einem Halbleiter mit der fundamentalen Bandlücke auf sich hat. Dies und noch mehr schauen wir uns im nächsten Modul näher an.
		Zu diesem Abschnitt gibt es derzeit weder eine Übungsaufgabe noch schnelle Fragen.

© H. Föll (MaWi für ET&IT - Script)