|
Mehr zu Bändern |
| |
 |
Wir hatten außer dem Fall des Na-Kristalls noch ein weiteres
Beispiel zu den Effekten, die beim Überlagern der Elektronenpotentiale in Atomen auftreten, und den hatten wir
uns beim Silizium angeschaut: |
| |
|
|
 |
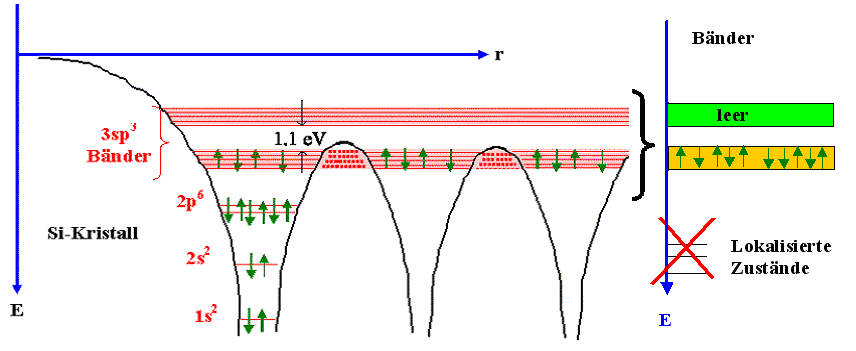
Es ist hier leicht modifiziert gezeigt. Um Zeichenarbeit zu sparen, malen wir zukünftig
nur noch den interessanten Teil – nur die Bänder, die die (im Prinzip beweglichen) Elektronen enthalten, oder
aber auch ganz leer sein können. Den Rest lassen wir weg, elektrisch sind die am Atom lokalisierten Elektronen sowieso
"tot"; sie können nichts tun. |
|
 |
Im Bild oben überlagern sich die letzten besetzten Zustände des einzelnen Si-Atoms (die
sind vom Typ 3sp3) so, daß zwei durch eine Energielücke
der Größe 1,1 eV getrennte Bänder entstehen. Wer mal genauer sehen will, wie das geht, betätigt
den Link. |
 |
Warum macht Si (und Ge und GaAs, und ...) so was? Nun ja – warum
eigentlich nicht? |
|
 |
Wir haben bisher keinerlei Hinweise darauf, was genau passiert, wenn Energieniveaus für
Elektronen von Herrn Pauli gezwungen werden aufzuspalten. Wir werden gleich ohne große Rechnungen (um ein paar kleinere
kommen wir nicht herum) noch einiges dazu lernen; hier nehmen wir aber schon mal zur Kenntnis: |
| |
(Fast) Nichts ist unmöglich!
E. Schrödinger
|
|
|
 |
Eine Bandlücke, d. h. ein Bereich auf der Energieachse
mit Zustandsdichte = null, kann bei der Überlagerung von Atomzuständen auftreten; die Größe
der Energielücke kann Bruchteile von eV oder mehrere eV betragen. |
|  |
Da wir das selbst nicht ausrechnen können, nehmen wir einfach mal hin, daß andere das können
und getan haben; im Zweifel hat man es gemessen. Wir nehmen außerdem auch noch zur Kenntnis, daß typischerweise
in einem Band alle Elektronen Platz haben, die unterzubringen sind, oder sogar doppelt so viele. |
 |
Damit könnten wir jetzt bereits alle Materialien bezüglich ihrer Leitereigenschaften
klassifizieren. Das ist aber nicht die einzige Eigenschaft, die aus der Bandstruktur folgt, daher wollen wir noch etwas
in die Tiefe gehen; auf die Leitereigenschaften kommen wir erst im nächsten Unterkapitel zurück. |
| | |
|
Freies Elektronengas und Beugung am Kristallgitter |
| |
 |
Um zu klären, wie die so überaus wichtige Bandstruktur zustandekommt,
sind die Elektronen vollquantenmechanisch zu behandeln – d. h. als Wellen zu beschreiben; die zugehörige Wellengleichung
ist die Schrödingergleichung. |
|
 |
Die Schrödingergleichung kann alles beschreiben, wofür man das Potential
angeben kann. Bislang hatten wir den allereinfachsten Fall besprochen: ein homogenes Kastenpotential, in dem Elektronen
eingesperrt sind (siehe Übungsaufgabe 2.3-1). |
|
 |
Als Lösungen ergeben sich ebene Wellen mit Wellenvektor k,
der die Rolle einer Quantenzahl hat. Die zugehörigen
Energie-Eigenwerte (Gesamtenergie E) sind (quasi-)kontinuierlich verteilt, wobei die Energie proportional
zu |k|2 =: k2 ist; der Proportionalitätsfaktor ist der
Term 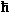 2/(2m) aus der Schrödingergleichung, so daß E = 2/(2m) aus der Schrödingergleichung, so daß E = 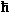 2k2/(2m). 2k2/(2m).
|
|
 |
Dies entspricht freien Teilchen, denn für solche ergibt sich mit dem Impuls
p = 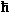 k (nach Herrn de Broglie) die kinetische Energie zu k (nach Herrn de Broglie) die kinetische Energie zu |
| |
Ekin = ½mv2 = p2/(2
m) = 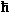 2k2/(2m) = E 2k2/(2m) = E |
|
|
|
 |
Das bedeutet, daß die gesamte Energie der Elektronen,
wie sie anhand der Schrödingergleichung berechnet wurde, als kinetische Energie vorliegt – und das ist nur bei
freien Teilchen der Fall. Denn sobald potentielle Energie beteiligt ist, geht diese auf irgendeine permanente Wechselwirkung
zurück – was bedeutet, daß die Teilchen nicht völlig frei sind. |
 |
Feine Sache – aber was soll das mit unseren Leitungsband- und Valenzbandelektronen
zu tun haben? Die sind ja alles andere als frei, denn zum einen sind sie im Kristall eingesperrt, zum anderen sind ihnen
die Atome im Weg, und mit denen können sie wechselwirken. |
 |
Den ersten Einwand, daß unsere Elektronen im Kristall eingesperrt sind,
haben wir bereits abgehandelt: Das Kastenpotential entspricht ja gerade dem Kristall als "Elektronenkäfig";
nur innerhalb des Kristalls verhalten sich die Elektronen wie freie Teilchen. Um den zweiten Einwand, daß da ständig
Atome im Weg sind, müssen wir uns nun kümmern. |
|
 |
Zum Glück ist das wegen der Symmetrie des Kristalls kein großes Problem:
Innerhalb des Kristalls weist das Potential dort, wo die Atome sitzen, den bekannten atomaren Potentialtrichter auf; oben
war es für Silizium noch einmal gezeigt. Weil es sich um einen Kristall handelt, sind diese Potentialtrichter periodisch
angeordnet, und daher ist das Potential in der Schrödingergleichung periodisch; diese Periodizität wiederum überträgt
sich auf die Lösung der Schrödingergleichung. |
|
 |
Die Lösung der Schrödingergleichung ist bekanntlich die gesuchte Wellenfunktion.
Bei den freien Elektronen sind das ebene Wellen, und diese ebenen Wellen sind bereits periodisch. Durch das periodische
Potential werden sie nur leicht modifiziert; diese modifizierten ebenen Wellen sind als Bloch-Funktionen bekannt. (Wer Näheres
dazu erfahren möchte, betätigt diesen Link;
der Rest braucht sich nicht mal den Namen zu merken.) |
|
 |
Das Fazit ist an dieser Stelle einfach, daß die freien Elektronen eine
gute Näherung für die tatsächlich im Kristall befindlichen Leitungselektronen darstellen. Man spricht daher
immer von den Leitungselektronen im Kristall als quasi-freien Elektronen. |
 |
Halt: Es ist zwar einerseits sehr erfreulich, daß man mit der Vorstellung
von (quasi-)freien Elektronen so weit kommt, es kann aber noch nicht der Weisheit letzter Schluß sein, denn eine Welle,
die sich durch eine periodische Struktur bewegt, wird daran gebeugt – und das gilt auch für Elektronen. |
|
 |
Zur Erinnerung hier noch mal das Bildchen dazu: |
|
|
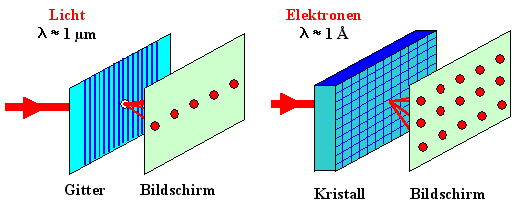 |
| Beugung von Licht am optischen Gitter |
Beugung von Materiewellen am Kristallgitter |
|
 |
Wir kommen also nicht umhin, die Beugung am Kristallgitter näher zu
betrachten – denn auch die Elektronen, die sich im Kristallgitter befinden, werden an demselben gebeugt. |
|
 |
Wir gehen aber nicht voll quantitativ vor und lösen die Schrödingergleichung
für ein periodische Potential, das die reale Situation in einem Kristall widerspiegelt, denn der dazu nötige Aufwand
ist erheblich. Für unsere Zwecke reicht es, die Lage mehr qualitativ zu betrachten, d. h. mit möglichst wenigen
Änderungen im Vergleich zum freien Elektronengas. |
|
 |
Dazu denken wir uns zwar ein periodisches Potential eingeschaltet, aber nur ein
ganz kleines. So klein, daß wir nur mit kleinen Korrekturen zu den Lösungen für ein konstantes Potential
zu rechnen haben, aber nicht mit grundsätzlich neuen Dingen. Wir betrachten dabei ausschließlich die generellen
Effekte, die durch Beugung zustandekommen. |
|
 |
Und wir nutzen vor allem aus, daß wir etwas Periodisches (eine Welle) an
etwas Periodischem (dem Kristallgitter) beugen – dazu gibt es nämlich bereits eine recht übersichtliche
Theorie.
|
|
Die Bragg-Bedingung der Beugung |
| |
 |
Bei der Beugung von Wellen interessiert man sich letztlich nur für die Fälle
konstruktiver Interferenz der von den Atomen ausgesandten Sekundärwellen, die, einzeln betrachtet, Kugelwellen
sind. (Die einfallende Welle, die an den Atomen gestreut wird, ist die Primärwelle.) |
|
 |
Damit ist klar: Es kommt auf den Gangunterschied zwischen den Sekundärwellen
an, und weil wir an etwas Periodischem (dem Kristallgitter) beugen, kann die Interferenz nur dann konstruktiv sein, wenn
der Gangunterschied für alle Atome einer Netzebene den gleichen Wert hat. |
|
 |
Die Erfahrung sagt, daß dann das Reflexionsgesetz "Ausfallswinkel = Einfallswinkel"
gilt. Als Erklärung dafür soll hier ein Plausibilitätsargument genügen (die volle Mathematik wäre
zu aufwendig): Andere Ausfallswinkel treten nicht auf, weil in diesen anderen Richtungen gestreute Wellen mit allen möglichen
Phasen auftreten; addieren wir die auf, ist das Resultat = 0. |
|
 |
Also konkret: Die Primärwelle sei eine ebene Welle mit Wellenvektor k,
und es existiere aufgrund konstruktiver Interferenz eine Sekundärwelle mit Wellenvektor k' –
wie in der folgenden Abbildung gezeigt (durch die Symmetrie haben wir in der Zeichnung das Reflexionsgesetz bereits berücksichtigt): |
| |
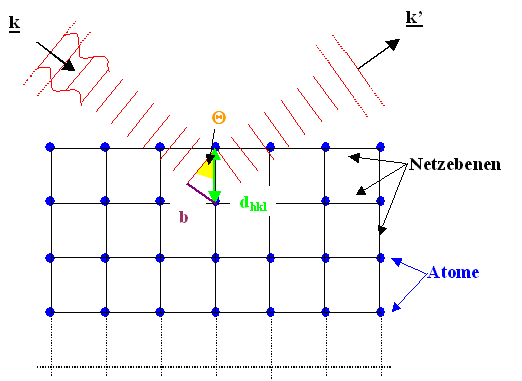 |
| Bragg-Bedingung erfüllt: Sekundärwelle aufgrund konstruktiver Interferenz |
|
|
 |
Der Netzebenenabstand ist dhkl; wir können ihn leicht aus den
Miller-Indizes berechnen. Der Gangunterschied zwischen
Wellen, die an benachbarten Netzebenen gestreut wurden, beträgt 2b; er hängt über den Winkel
Q
mit dem Netzebenenabstand zusammen. Wie hängen diese Größen im Fall konstruktiver Interferenz mit der
Wellenlänge lder zu streuenden Welle zusammen? |
|
 |
Das ist einfach: Konstruktive Interferenz tritt dann und nur dann auf, wenn der Gangunterschied
2b zwischen den an zwei benachbarten Netzebenen gestreuten Wellen genau ein Vielfaches der Wellenlänge
l beträgt. Also: |
|
|
| 2 · b | = |
n· l | |
n=1, 2, 3, ... | | | |
| | | | b |
= | dhkl · sinQ |
| |
|
|
|
 |
Damit ergibt sich für den spezifischen Winkel QB,
bei dem (und nur bei dem) Reflexion stattfindet, die gesuchte Bragg-Bedingung: |
| |
| 2 · dhkl · sinQ
B | = | n · l |
| sinQ B | = |
n · l
2 · dhkl |
|
|
 |
Eine simple, aber bemerkenswerte Gleichung! Bemerkenswert ist vor allem dies: |
|
 |
Wenn die Bragg-Bedingung nicht erfüllt wird, läuft
die Welle unverändert durch den Kristall. Das bedeutet, daß ein Elektron
mit einer solchen Ausbreitungsrichtung dann nichts von den anwesenden Atomen spürt! |
|
 |
Für n · l > 2 · dhkl
können keine Lösungen existieren, d. h. für Wellenlängen, die größer
sind als zweimal die Gitterkonstante a, gibt es schlicht keine Möglichkeit der konstruktiven Interferenz
(denn das größtmögliche dhkl = a haben wir für die {100}-Ebene).
Auch ein solches Elektron spürt nichts von den Atomen. |
|
 |
Wie wir bald sehen werden, betrifft dieses Nichts-von-den-Atomen-Spüren praktisch alle
für uns relevanten Leitungselektronen! |
 |
Außerdem gilt offenbar, daß eine
Ebenenschar viele Sekundärwellen hervorrufen kann – je nachdem, welche ganze
Zahl n wir wählen. |
|
 |
Letzteres können wir aber auch anders interpretieren, indem wir das n dem
dhkl
zuordnen: Für n = 1, 2, 3, ... können wir auch dhkl
, ½dhkl, (1/3)dhkl usw. schreiben. |
|
 |
Die Sekundärwelle 2. Ordnung (d. h. die für n = 2)
schreiben wir damit nicht der Ebenenschar {hkl} zu, sondern der Schar {2h 2k 2l}, die Sekundärwelle 3.
Ordnung (d. h. die für n = 3) der Schar {3h 3k 3l} usw. Auch deswegen wurde bei der
Einführung der Miller-Indizes das "Kürzen"
nicht erlaubt, d. h. wir unterscheiden zwischen der {111}-Ebene und der {222}-Ebene usw.
|
|
Die Bragg-Bedingung in Vektorschreibweise |
|
|
 |
Das Bragg-Gesetz in obiger Formulierung ist eine Skalargleichung, in der statt
dem Wellenvektor die skalare Wellenlänge steht. Eine Vektorgleichung wäre
automatisch sehr viel allgemeiner und mächtiger; wir wollen deshalb jetzt das Bragg-Gesetz auf Wellenvektoren
umschreiben. Das machen wir zunächst etwas unmathematisch durch eine Plausibilitätsbetrachtung.
|
|
 |
Dazu betrachten wir nochmals das obige Prinzipbild: Wir haben eine einfallende Welle, vollständig
charakterisiert durch ihren Wellenvektor k (und die hier uninteressante Amplitude), und eine gebeugte
Welle mit k'. Da wir nur elastische Streuung betrachten, d.
h. keine Energieänderungen zulassen, gilt immer |
|
|
|
|
 |
Eine Vektorbeziehung zwischen k und
k' kann dann im einfachsten Fall zum Beispiel so aussehen: |
| |
|
|
 |
Dabei ist G ein zunächst noch undefinierter Vektor, in dem "irgendwie"
das Gitter steckt, an dem die Welle gebeugt wird. Da die Wellenvektoren aber nicht im "normalen" Raum definiert
sind (denn sie sind vom Typus "1 / Länge" und haben die Maßeinheit m–1), ist
auch G ein Vektor in diesem "anderen Raum". |
 |
Falls wir den Vektor G immer so definieren können, daß
für ein gegebenes Gitter alle Varianten der skalaren Bragg-Bedingung erfüllt sind, haben wir die gesuchte Vektorformulierung
gefunden. |
|
 |
Das ist einfach. Wir müssen nur die Vektorgleichung in Komponenten hinschreiben, um sofort
zu sehen, wie sich G bestimmt. Das folgende Bild hilft dabei: |
| |
|
|
 |
Wir wollen die Situation möglichst einfach beschreiben und wählen dazu das Koordinatensystem
möglichst günstig. Als z-Richtung nehmen wir die Senkrechte auf der betrachteten Ebenenschar, und die x-Richtung
legen wir in die Richtung, in der k von der Senkrechten abweicht. |
|
 |
Wegen des Reflexionsgesetzes gilt für die Komponenten von G offenbar
(da die y-Komponente keine Rolle spielt, lassen wir sie komplett weg): |
| |
æ
è |
Gx
Gz |
ö
ø | = |
æ
è |
kx
kz |
ö
ø | – |
æ
è | k'x
k'z | ö
ø | = |
æ
è | 0
k· sinQ + k · sinQ |
ö
ø | = |
æ
è |
0
2k · sinQ |
ö
ø |
|
|
|
 |
Für sinQ verwenden wir die bereits abgeleitete skalare
Bragg-Bedingung (siehe oben) mit n = 1, weil wir uns hier auf die Ebenenschar {hkl}
beziehen (für n > 1 bezögen wir uns auf Zwischenebenen, siehe oben). Außerdem ersetzen
wir die Wellenlänge via l = 2p/|k| = 2p/k und erhalten so für die z-Komponente des Vektors G |
| |
| Gz = 2k· sinQ
| = | 2k· |
l
2 · dhkl |
= | k · |
2p
k · dhkl | = |
2p
dhkl |
|
|
 |
Die Bragg-Bedingung lautet in vektorieller Form
also vollständig so: |
| |
|
 |
In Worten bedeutet das: |
|
 |
Eine Welle mit einem beliebigen Wellenvektor k wird an der Ebenenschar
{hkl} dann und nur dann gebeugt, falls die Differenz von einfallendem und gebeugtem
Wellenvektor identisch ist zu einem Vektor Ghkl, der die Ebenenschar {hkl} symbolisiert.
|
|
 |
Der Vektor Ghkl hat zwei einfache Eigenschaften,
die ihn eindeutig bestimmen:
1.) Ghkl
steht senkrecht auf der Ebenenschar {hkl}.
2.) Die Länge von Ghkl ist proportional zum reziproken Abstand der Netzebenen, es gilt immer |
| |
|
| |
|
 |
Im nächsten Modul schauen wir uns die Konsequenzen der Eigenschaften von
Ghkl für unsere Elektronenwellen näher an.
|
| |
Zu diesem Abschnitt gibt es derzeit weder eine Übungsaufgabe noch schnelle Fragen.
|
© H. Föll (MaWi für ET&IT - Script)