 |
Das in die Schrödingergleichung einzusetzende Potential haben wir schon
mal gezeichnet: |
| |
|
|
 |
Wir könnten das mal in einer ersten Näherung als eine Sinusfunktion ausdrücken
(oder gleich als Fourierreihe), in die Schrödingergleichung einsetzen und mal sehen, wie weit wir mit dem jetzt rein mathematischen Problem kommen. |
|
 |
Nicht weit. Also machen wir eine radikale Vereinfachung: Wir ersetzen das reale periodische
Potential durch ein mittleres konstantes Potential U = 0 eV, d. h. wir
legen auch den Energienullpunkt auf dieses Potenial. Außerdem schauen wir zunächst nur
die x-Richtung an, d. h. wir behandeln das Problem erst mal eindimensional |
| |
 |
Gegeben ist damit eine auch im 2. Semester lösbare eindimensionale
Schrödingergleichung mit
dem Potential: |
| |
| – |
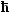 2 2
2me |
· |
d2y(x)
dx2 |
+ U(x) y(x) |
= | E y(x) |
| U(x) | = |
{ | U
0 = const. = 0 eV
¥ |
für 0 £ x
£ Lx
sonst |
|
|
|
 |
Wir haben damit sozusagen einen eindimensionalen "Modellkristall" der Länge
Lx postuliert. |
 |
Nun zur Aufgabe. |
 |
1. Zeige, dass die allgemeine eindimensionale Lösung (unter Benutzung
der Normierungsbedingung) die folgende Form hat: |
| |
| y(r) | = |
æ
ç
è |
1
Lx |
ö
÷
ø | 1/2 |
· exp | (i kx x) |
|
|
|
 |
Immer vorausgesetzt, daß gilt: |
|
|
| E | = |
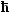 2 kx2 2 kx2
2me
|
|
|
 |
2. Zeige, daß wir damit auch die drei
dimensionale Lösung für einen Kristall der Ausdehnung Lx = Ly = Lz
= L
haben (unter Benutzung der dreidimensionalen Normierungsbedingung
), in der Form |
| |
| y(r) | = |
æ
ç
è |
1
L |
ö
÷
ø | 3/2 |
· exp | (i k · r) |
|
|
|
 |
Mit Wellenvektor k = (kx , ky,
k z) und Ortsvektor r. |
 |
3. Zeige, daß die unten angeführten Gleichungen für
den Wellenvektor
k sich aus den periodischen Randbedingungen
y(r + L) = y(r) ergibt. |
|
 |
(Wer Lust hat, darf auch gern alternativ für feste Randbedingungen
der Form y(0) = y (L) = 0 ausprobieren.) |
| |
| kx = ± | n
x · 2p
L |
| ky = ± |
ny · 2p
L |
| kz = ± |
nz · 2p
L |
|
|
|
 |
Dabei sind die nx,y,z offenbar die Quantenzahlen
mit denen die ¥
vielen Lösung durchnumeriert werden können; ihr Wertebereich ist 0, ±1, ±2, ... |
 |
4. Jetzt zu den schwierigen Fragen: |
|
 |
Was bedeutet diese Lösung für Elektronen im "Kristall" anschaulich? |
|
 |
Wo befindet sich das Elektron eigentlich? |
|
 |
Wo sind die Energeniveaus in diesem rechteckigen Potentialtopf? Die ersten 10
oder so kann man ausrechnen und einzeichnen. Wie groß ist dabei der Entartungsgrad, d. h. wieviel Elektronen haben
auf einem Niveau Platz? |
|
 |
Was passiert, falls wir mehr als ein Elektron betrachten? |
 |
Die Aufgabe mag schwierig erscheinen; das darin codierte "freie
Elektronengasmodell" ist aber das grundlegende Paradigma der gesamten Halbleiterei! Es wird uns nicht erspart
bleiben! |
| |
© H. Föll (MaWi für ET&IT - Script)
![]() 2.3.2 Wellenfunktion und Schroedingergleichung
2.3.2 Wellenfunktion und Schroedingergleichung ![]() 2.3.3 Zustaende, Wellen, Energie und Impuls
2.3.3 Zustaende, Wellen, Energie und Impuls ![]() 2.3.4 Merkpunkte zu Kapitel 2.3
2.3.4 Merkpunkte zu Kapitel 2.3 ![]() 8.2.3 Zustandsdichte und Bandluecke
8.2.3 Zustandsdichte und Bandluecke ![]() 8.2.1 Elektronenwellen im idealen Kristall
8.2.1 Elektronenwellen im idealen Kristall