 |
1. Was für eineWellenlänge l hat ein Teilchen der Masse m,
das mit der Geschwindigkeit v und damit dem Impuls p = mv seines Weges zieht. Die einfache Gleichung
dazu heißt auch de Broglie
Beziehung |
 |
Der Impuls p einer Welle war
p = 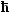 k = (h/2p) · 2p/l
= h/l := mv . k = (h/2p) · 2p/l
= h/l := mv . |
|
 |
Damit gilt für die Wellenlänge |
| |
|
|
 |
Das ist die mit Recht berühmte de Broglie Beziehung. |
|
| |
 |
2. Wie groß ist die Wellenlänge für Elektronen- bzw.
Protonstrahlen mit Energien von 10 eV, 10 keV und 1 MeV?
Was könnte man erwarten wenn diese
Wellen auf einen Kristall fallen? Hinweis: Was erwartet man für Lichtwellen mit l
» 1 µm wenn sie auf periodische Strukturen mit sehr viel größerer, kleinerer,
oder ungefähr passender "Gitterkonstante" fallen? |
 |
Da wir hier über rein kinetische Energie Ekin reden, gilt
E
kin ½ mv2 = p2/2m = eU . U ist
dabei dieBeschleunigungsspannung, eU die gewonnene kinetische Energie nach durchlaufen der Spannung U. |
|
 |
Daraus, und mit der obigen de Broglie Beziehung folgt sofort
|
| |
|
|
 |
Ein paar repräsentative Zahlenwerte für Elektronenstrahlen sind: |
| |
| Ue [V] |
le [nm] |
| 10 | 0.388 |
| 1 000 | 0.0388 |
| 10 000 | 0.0123 |
|
|
 |
Die Wellenlängen bei Protonenstrahlen sind nach der Formel um (mp/me)
½ » 43 mal kleiner |
|
 |
Was wird wohl passieren, wenn die Welle auf periodische Strukturen mit Gitterkonstante ungefähr
Wellenlänge fallen: Kräftige Interferenz und Beugung! |
| | | |
© H. Föll (MaWi für ET&IT - Script)