 |
Mit dem Input "Potential" und der Schrödingergleichung als "Datenverarbeiter"
erhalten wir als Output die möglichen Zustände des Systems, das wir berechnen; bisher war das immer ein
Elektron. |
|
 |
Ein Zustand wird durch eine
von typischerweise ¥ viel möglichen Wellenfunktionen plus
einer zugehörigen Gesamtenergie definiert. Die Sortierung der ¥ vielen Lösungen
erfolgt durch ein mehr oder minder umfangreiches System von Quantenzahlen. |
|
 |
Typischerweise tauchen in der Wellenfunktion Ausdücke der Form exp(ik·r)
auf. In der Reinform haben wir dann eine ebene Welle.
Die Größe k heißt Wellenvektor , sie enthält
die folgenden Informationen: - Ausbreitungsrichtung der Welle (in k-Richtung).
- Die Wellenlänge l = 2p/|k|.
- Den Impuls des durch diese Welle beschriebenen Elektrons; es gilt die De-Broglie-Beziehung
p =
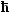 k. k. - Die Energie
E(k) des durch diese Welle beschriebenen Elektrons; aus dem De-Broglie-Impuls folgt die
(rein kinetische) Energie zu E(k) = (
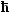 k)2/(2me). k)2/(2me).
|
|
 |
Alle Wellensorten könen durch geeignete Überlagerungen von ebenen Wellen
dargestellt werden. Die Bedeutung des Wellenvektors (oder dann der Wellenvektoren) bleibt erhalten, jedoch kann sich die
Energie-Impuls-Beziehung
, d. h. der funktionelle Zusammenhang E(k ) stark ändern. |
 |
In der formalen Beschreibung eines Zustands taucht die Zeit
nicht auf. Ein Elektron in einem Zustand tut so gesehen nichts, es existiert in zeitlich
unveränderlicher Form; nichts passiert. |
|
 |
Falls was passieren sollte, d.h. falls sich was ändern
sollte, hat sich nicht der Zustand geändert, sondern das Elektron hat seinen Zustand gewechselt
. Es wird jetzt durch eine andere Wellenfunktion beschrieben und hat, wenn sich wirklich was ändern soll, jetzt
auch eine andere Energie. |
|
 |
Die interessanten Zustandsänderungen bedingen damit Energieaufnahme oder -abgabe, und
das immer in Quanten, die zum Abstand der Energieniveaus passen. |
 |
Der Energieerhaltungssatz erzwingt einen Partner für Zustandsänderungen.
Die Energie muss von "jemand" kommen oder an "jemand" gehen. Die Auswahl an Partnern für die uns
interessierenden, im Kristall herumlaufenden "freien Elektornen" ist aber begrenzt; wir haben nur :
- Atomkerne (aus Protonen und Neutronen zusammengesetzt) + Elektronen = Atome oder Ionen = "der Kristall" für
uns.
- Andere (freie) Elektronen.
- Photonen = "Lichtteilchen".
|
 |
Das war's. In den drei Möglichkeiten steckt alles, was uns in dieser Vorlesung
interessiert: |
|
 |
Die Nummer 1 koppelt die Vibrationen der Kristallatome oder ihre thermische Energie an die freien Elektronen, die im Leiter und Halbleiter den Strom tragen. Hier kommt die
Temperatur als wesentlicher Parameter ins Spiel. |
|
 |
Die Nummer 2 ist trickreich. Unser
Elektron muss die anderen Elektronen vermeiden wie die Pest – es gilt das Pauli-Prinzip. Das ist entscheidend für die Stromleitung und viele andere Materialeigenschaften. |
|
 |
Hinter der Nummer 3 verbirgt sich die Solarzelle, die "light emitting diode"
oder LED, der Halbleiter-Laser und so ziemlich alles, was entfernt mit Licht zu tun hat. |
 |
Deswegen müssen wir uns mit den Grundlagen der Quantentheorie beschäftigen.
Man (und frau) kann moderne ET&IT sonst nicht mal ansatzweise verstehen. |
| | |
|
Laufende ebene Wellen
|
| | |
 |
Dieser Abschnitt gibt die Essenz dieses bereits mehrfach
empfohlenen Links wieder. |
 |
In der Übungsaufgabe 2.3-1
haben wir für die Wellenfunktion eines Elektrons, multipliziert mit dem Phasenfaktor
±exp(i w t), eine laufende ebene Welle bekommen, beschrieben durch
|
| |
| y(r,t) | =
|
A exp(i k · r) exp(±i wt) |
= |
A exp[i (k · r ± wt)]
|
|
|
|
 |
Je nach Vorzeichen ± innerhalb des Phasenfaktors läuft die Welle
nach links oder rechts (selbst überlegen, warum). Wir nehmen jetzt das Minuszeichen. |
 |
Wir nehmen das mal als typisch für Wellenfunktionen und schauen uns an, was
das bedeutet. Falls wir erst mal nur den Realteil verwerten, erhalten wir |
| |
| Re y (r ,t) | = |
A cos(k · r – wt)
|
|
|
|
 |
Es handelt sich um eine laufende ebene Welle,
da sich die Phase wt linear mit der Zeit ändert. Zu jedem Zeitpunkt ti
sieht man eine Momentaufnahme der Welle; etwas später, zum Zeitpunkt
ti + Dt, hat sich der Cosinus etwas "verschoben" –
die Welle "läuft", wie weiter unten dargestellt. |
|
 |
Für den Imaginärteil gilt natürlich im Prinzip dasselbe; davon
lernen wir nichts Neues. |
 |
In der Quantenmechanik betrachten wir nicht nur den Realteil, denn die Wellenfunktion
ist eine intrinsisch komplexe Funktion, d.h. nicht nur aus Gründen der Schreibökonomie. |
|
 |
Physikalische Bedeutung hat aber (für uns) nur das Betragsquadrat
der Wellenfunktion , |y|2 = y
y*; und das ist eine reelle Funktion oder Zahl. Wir
erhalten: |
| |
|
 |
Das Betragsquadrat dieser Wellenfunktion ist
also eine Konstante, r und t "fliegen raus". Deswegen kann man den Phasenfaktor
getrost immer gleich weglassen. |
|
 |
Damit ist die Aufenthaltwahrscheinlichkeit des Elektrons im betrachteten Raum überall
gleich. Unten ist die Wellenfunktion für zwei verschiedene Zeiten und die Aufenthaltswahrscheinlichkeitsdichte
|y|2 dargestellt. |
|
|
|
| | |
|
Stehende Wellen |
| | |
 |
Wer die Übungsaufgabe 2.3-1
auch für feste Randbedingungen (richtig)
gerechnet hat, wird als Lösung der Schrödingergleichung stehende Wellen bekommen
haben. |
|
 |
Stehende Wellen erhält man immer, indem man zwei in entgegengesetzte Richtungen laufende
Wellen überlagert. Die Formel dazu sieht so aus: |
|
|
| y( r,t) | = |
exp( + i k · r) exp(iw
t) ± exp(– i k · r ) exp(iwt) |
|
|
 |
Wie man die Überlagerung macht, ist egal – daher das "±"-Zeichen.
|
|
 |
Betrachten wir den Fall mit der additiven Überlagerung der beiden Wellen, so ergibt
sich |
| |
| y(r,t) | = |
2 cos(k · r) exp(iw t) |
|
|
|
 |
Der Realteil dieser Funktion zeigt wiederum die Eigenschaften dieser Welle: |
| |
| Re y(r,t) | = |
2 cos(k · r) cos(wt) |
|
|
|
 |
Das Betragsquadrat der Wellenfunktion , also die quantenmechanische
Aufenthaltwahrscheinlichkeit(sdichte) von z. B. einem Elektron, ist nun nicht mehr konstant im Raum, sondern gegeben durch |
| |
|
|
 |
Und das sieht für zwei stehende Wellen y
1 und y2, mit Frequenzen n1
und n2 = 2n1 (oder k2 =
2k1), so aus (die rote Kurve ist y1): |
| |
|
|
 |
Die Wahrscheinlichkeitsdichte hat jetzt Maxima und Minima, an denen sie = 0 ist. |
| |
|
|
Kugelwellen
|
| |
|
 |
Kugelwellen sind Wellen, die sich von einem Punkt aus in alle Richtungen gleichförmig
ausbreiten. Zweidimensional kennt das jede und jeder, die/der schon mal einen Stein ins Wasser geworfen hat. |
|
 |
In der Welt der Physik/Materialwissenschaft treten Kugelwellen aber auch auf, wenn man z.B.
Licht (oder Elektronenwellen oder Phononen [= Gitterschwingungen] oder ...) an einem "punkt"förmigen Streuzentrum
(ein Atom, ein anderes Elementarteilchen, eine Ausscheidung ...) – nun ja, halt streut.
|
|
 |
Jedes denkbare Streuzentrum ist hinreichend punktförmig, sobald es viel kleiner ist als
die Wellenlänge der Welle, die gestreut wird. |
 |
Die gestreute Welle wird im Nahfeld, d.h. in der Nähe des Streuzentrums,
beschrieben durch |
| |
| y (| r |, t) = |
1
| r | |
exp [i (|k | | r| + wt)] |
|
|
|
 |
Und das sieht so aus: |
|
|
|
| |
|
|
Elektron als Wellenpaket |
| | |
 |
Wie beschreibt man nun ein einzelnes Elektron,
Proton, Neutron (oder, falls wir gleich verallgemeinern: ein Atom, viele Atome; Herrn Schröder, das Universum), das
wir nicht als Lösung der Schrödingergleichung bekommen, sondern von dem wir einfach wissen
, daß es sich irgendwo (d.h. an einem halbwegs definierten Ort) befindet und
das keinesfalls überall gleichzeitig sein kann. Außerdem wird es evtl. auch noch mit einem halbwegs definierten
Impuls herumlaufen. |
|
 |
Eine unendlich ausgedehnte ebene Welle mit überall konstanter Aufenthaltswahrscheinlichkeit
kann das einfach nicht leisten. |
 |
Wir beschreiben das so, dass wir den Ebene-Welle-Term exp(ik·r
) beibehalten, aber das Teilchen trotzdem halbwegs lokalisieren. |
|
 |
Wir betrachten jetzt also ein Elektron, das aus irgendwelchen Gründen nicht mehr gleichmäßig
über den ganzen Raum verschmiert ist, sondern in einem mehr oder weniger präzise definierten Raumbereich lokalisiert ist. |
|
 |
Es hat dann keinen reinen Wellencharakter mehr, sondern
es verhält sich auch wie ein Teilchen, da es nur in einem bestimmten Raumbereich eine endliche Aufenthaltswahrscheinlichkeit hat.
|
 |
Rein mathematisch beschreiben wir das mit einem Wellenpaket
, das wir durch eine Überlagerung von ¥ vielen Wellen erhalten. |
|
 |
Dazu nehmen wir Wellenvektoren mit verschiedenen Amplituden; d.h. A = A(k)
aus einem Intervall [k – Dk/2 , k + Dk/2]
|
|
 |
Die ¥ vielen Wellen werden aufaddiert oder integriert;
wir erhalten |
| |
| y(| r |, t) = |
k + Dk/2
ó
õ
k – Dk/2 |
A(k') exp[i (k' · r + wt)] dk' |
|
|
|
 |
Jetzt darf es im Kopf klingeln: Das sieht nicht nur wie eine Fouriertransformierte aus, sondern das ist die Fouriertransformierte des "Spektrums", der Verteilung
der Amplituden auf die k-Werte (und damit auch auf die Frequenzwerte). Wer nun die Fouriertransformation (noch)
nicht kennt, hat allerdings keinen Nachteil davon, daß es bei ihm nicht klingelt. |
 |
Was dabei rauskommt, sieht etwa so aus: |
| |
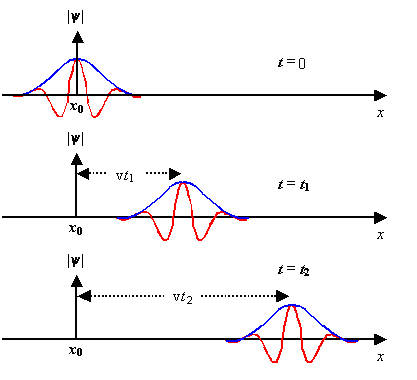 |
Elektron als Wellenpaket zu verschiedenen Zeiten.
Der Realteil
der Wellenfunktion ist rot dargestellt,
die Wahrscheinlichkeitsdichte (= Betrag yy*) ist blau. |
|
|
 |
Kann man das einfach verstehen? Ja - wir brauchen nur einen Haufen Cosinüsse
mit verschiedenen Wellenlängen zu nehmen, die wir so überlagern, daß bei x = 0 alle den Wert
1 haben. |
|
 |
Die Überlagerung produziert dann bei x = 0 einen ziemlich großen
Wert, aber etwas entfernt davon gibt es nur noch ein wildes Gewusel aller möglichen Werte, die sich gegenseitig aufheben. |
|
 |
Etwas vornehmer (und möglicherweise für Zweitsemester unverständlich) ausgedrückt:
Die Fouriertransformierte einer Deltafunktion enthält alle Frequenzen von 0 bis ¥
mit gleicher Amplitude. Engen wir den Frequenzraum ein (indem wir z.B. die Amplitude mit wachsendem Abstand von einer Grundfrequenz
auf 0 fahren), ergibt sich ein Wellenpaket. |
 |
Das Wellenpaket beruht also darauf, daß ein Bereich von Wellenvektoren
mit einer "spektralen Breite" von Dk
beiträgt. Im Ortsraum hat das Wellenpaket eine laterale Ausdehnung von Dx.
|
|
 |
Im Sinne der Quantenmechanik handelt es sich dabei um die Unschärfen der jeweiligen
Größen. Bemerkenswerterweise liefert die Theorie der Fouriertransformation, daß das Produkt dieser Unschärfen
bei einem sog. Gaußschen
Wellenpaket konstant ist. Diese Tatsache kann physikalisch sofort verstanden werden: Mit Dk
ist die Impulsunschärfe D
p = 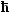 Dk verbunden, und nach der Unschärferelation
ist das Elektron daher auf einen endlichen Raumbereich Dx beschränkt. Dk verbunden, und nach der Unschärferelation
ist das Elektron daher auf einen endlichen Raumbereich Dx beschränkt.
|
|
 |
Dies steht im Gegensatz zum Elektron als laufende Welle, das im gesamten Raum verteilt ist
– denn mit Dk
® 0 ist Dx ®
¥ verbunden. |
|
|
|
Was können Wellen, was Teilchen nicht
können? |
| |
|
 |
In der klassischen Physik gibt es nicht nur Teilchen, es gab immer auch schon
Wellen – z. B. elektromagnetische Wellen, Wellen in Wasser und akustische Wellen. |
|
 |
In der Tat: Bläst man in eine Orgelpfeife oder Flöte
der Länge L , regt man eine stehende Welle im Druck
p der folgenden Form an: |
|
|
| p(x , t) | = |
p0 |
exp(+ i k x) exp(i w
t) ± exp(– i k x) exp(i w t) |
| | | | |
| k | = |
2 pn /L oder nl = L |
| | | | |
| n | = |
1, 2, 3, 4, ... |
|
|
|
 |
In anderen Worten: In der Orgelpfeife (oder auf der Violinsaite) können nur Wellen "leben",
deren Wellenlängen l exakt in die Länge L der Pfeife (bzw. der
Saite) passen. |
|
 |
Bläst man in ein kugelförmiges Musikinstrument (z. B. eine Okarina), regt man ... – genau! Man regt nahe Verwandte der Kugelflächenfunktionen
des Wasserstoffatoms an! Deshalb war die Mathematik des Wasserstoffatoms schon vor seiner "Erfindung"
bekannt! |
|
 |
Was also ist neu? Nun – alles! Teilchen können jetzt einiges, was sie klassisch
niemals könnten:
- Sie können interferieren, d. h. sich gegenseitig verstärken oder auslöschen – auch mit sich selbst!
- Sie können an periodischen Strukturen gebeugt werden.
- Sie werden von Hindernissen beeinflusst, die sie auf ihrer Flugbahn gar nicht tangieren.
- Sie können durch massive Wände einfache "tunneln".
- Sie können "überall" gleichzeitig sein (wo genau "ist" denn eineWelle?).
- Sie können auf Randbedingungen wie "Flötenlänge" reagieren und nur noch diskrete Zustände
einnehmen.
|
 |
Eine Frage müßte sich aufdrängen: Was für eine Wellenlänge
hat denn ein Teilchen (wie z. B. ein Elektron)? Das kann man mit dem schon Gelernten selbst herausfinden! |
| |
|
 |
OK – gehen wir mal ganz kurz durch die obige Liste. Und was folgt, sind
nicht Spekulationen, sondern durch zahllose Experimente bis ins Kleinste bestätigte Fakten. |
 |
Interferenz von Teilchen
|
|
 |
Teilchen als Teilchen laufen mit konstantem v
gegen eine Wand mit zwei schmalen Schlitzen. Entweder laufen sie durch die Schlitze, oder sie werden reflektiert. Hinter
der Wand findet man Teilchen nur exakt hinter den Schlitzen (mit "Wahrscheinlichkeit" w = 1) und
sonst nirgendwo (d. h. mit "Wahrscheinlichkeit" w = 0). |
| |
|
|
 |
Teilchen als (ebene) Welle (oder wer's lieber hat: als
Wellenpakete) laufen mit konstantem k gegen eine Wand mit zwei schmalen Schlitzen. Jedes Teilchen läuft
gleichzeitig durch beide Schlitze und interferiert mit sich selbst. Die Wahrscheinlichkeit,
das Teilchen hinter der geschlitzten Wand zu finden, sieht aus wie ein typisches Interferenzmuster, denn es ist ein Interferenzmuster. |
 |
Beugung an periodischen Strukturen
|
|
 |
Ein optisches Gitter ist eine periodische Struktur; Licht wird daran gebeugt
, falls die Gitterkonstante und die Wellenlänge ähnliche Größenordnungen
haben – d. h. beide im µm-Bereich liegen. |
|
 |
Ein Kristall ist eine periodische Struktur mit einer Gitterkonstante im Ongström-Bereich
(1 Å= 0.1 nm). Materiewellen werden daran gebeugt, falls ihre Wellenlänge
ebenfalls in diesem Bereich liegt – was sie für Elektronen tut, wie wir wissen, falls wir Aufgabe
2.3-2 gemacht haben. |
| |
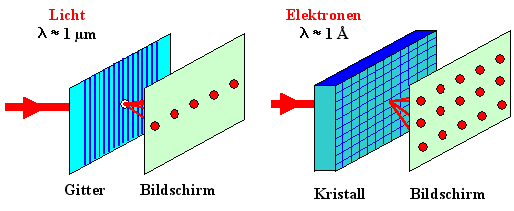 |
| Beugung von Licht am optischen Gitter |
Beugung von Materiewellen am Kristallgitter |
|
|
 |
Was für die Elektrotechnik der Oszillograph, ist für die Materialwissenschaft die
Beugung von "Teilchenwellen" oder Materiewellen am Kristall. Wir werden das später brauchen und ausführlicher
besprechen. |
 |
Eigentlich nicht vorhandene Hindernisse und der Tunneleffekt |
|
 |
Kommt ein Teilchen geflogen, auf der Höhe h0
, mit der kostanten Geschwindigkeit v. Dann ist da noch eine knallharte Mauer mit der Höhe h <
h0
(Bilder oben) oder h > h0 (Bilder unten). Schaun' mer mal, was klassischen Teilchen
und Teilchenwellen dabei so passiert. |
|
|
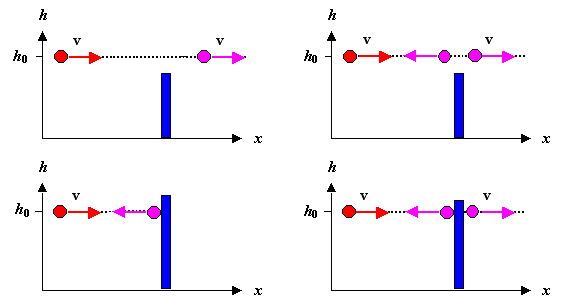 |
| Klassisches Teilchen und Mauer |
Materiewelle und Mauer |
|
|
 |
Was ein klassisches Teilchen macht, ist völlig klar: Es fliegt entweder über die
Mauer und nimmt sie dann überhaupt nicht wahr, oder es knallt dagegen und wird reflektiert. Eine Materiewellen dagegen
macht sehr merkwürdige Dinge:
- Es nimmt die Mauer auch dann wahr, wenn es problemlos drüberfliegen könnte. Ein Teil der Welle wird reflektiert,
der Rest fliegt weiter.
- Falls es tief genug fliegt, um gegen die Mauer zu knallen, wird es zwar reflektiert, aber nur zum Teil, der Rest "tunnelt"
durch die Mauer und fliegt auf der anderen Seite weiter. Wir haben den Tunneleffekt
.
|
|
 |
Wie darf man das verstehen? Schlicht und ergreifend so, dass die Betragsquadrate der Wellenfunktionen
für die Zustände "Reflektiert, obwohl es drüber
paßt" (= y
r, d) und "Durchgetunnelt, obwohl es k nallt"
(= yd, k) nicht null sind. Es besteht eine endliche Wahrscheinlichkeit dafür,
das (ganze) Teilchen mit v oder –v rechts oder links der Mauer zu finden. Wie groß diese Wahrscheinlichkeiten
sind (d. h. die Zahlenwerte von |yr, d|2 und |yd,
k|2), hängt von der Höhe und (vor allem) der Dicke der Mauer ab (sowie von der Masse des
Teilchens!). |
|
 |
Der Tunneleffekt scheint ziemlich exotisch zu sein. Der Schein trügt! Er kommt in jedem
modernen Mikroelektronik-Chip und in vielen anderen ET-Produkten sehr stark zum Tragen! |
 |
Wellen können überall gleichzeitig sein |
|
 |
Ein klassisches Teilchen ist entweder hier oder dort – mit hoher Präzision. Von
hier nach dort kommt es durch eine entsprechende Bewegung; dazu braucht es eine Zeit Dt,
die man ausrechnen kann – und die nicht beliebig klein sein kann, sagt A. Einstein. |
|
 |
Wo ist denn eine ebene Welle y
0 ~ exp(i k · r) gerade? Oder Dt
später? Wie wir in Übung 2.3-1 (hoffentlich) ausgerechnet
haben, ist die Aufenthaltswahrscheinlichkeit y0
y0* = |y
0|2 für das zugehörige Teilchen überall konstant. |
|
 |
Was bedeutet konkret eine Aussage wie "die Aufenthaltswahrscheinlichkeit ist überall
konstat und = 0,1"? Wenn ich eine Messung an einem definierten Ort mache, finde ich ja keine Zehntelteilchen,
sondern mein Messinstrument sagt mir eindeutig, "das Teilchen war zum Zeitpunkt t0 der Messung
bei (x0, y 0, z0) entweder komplett da oder komplett nicht
da". So ist das auch – der Detektor registriert entweder ein komplettes Teilchen oder gar keines. Wenn ich für
unser Beispiel 1000mal messe, wird es etwa 100mal da sein und 900mal nicht. Genau wie auch sonst in
der Stochastik: Ein Würfel gibt jede Zahl auf seinen Seitenflächen mit der gleicher Wahrscheinlichkeit 1/6,
aber bei jedem Wurf eben nur eine einzige wohldefinierte Zahl. |
|
 |
Wie ist das bei anderen Wellen? Exakt so wie bei "gezinkten" Würfeln. Die Wahrscheinlichkeiten
sind nicht mehr überall gleich, sondern wir haben jetzt eine Aufenthaltswahrscheinlickeit
|y0(x, y, z, t)|2
, die eine Funktion des Ortes und vielleicht auch der Zeit ist. |
|
 |
Man könnte sich natürlich ein Wellenpaket nach obigem
Vorbild auch so konstruieren, dass nur ein scharfer Peak vorhanden ist (mit minimalen "Unterschwingern").
Dann weiß man ziemlich genau, wo sich das Teilchen befindet; man hat es bis auf ein kleines Dx
lokalisiert. Aber je schärfer defniert, desto mehr Wellen mit exp(i kn
x) mit verschiedenen kn muss ich überlagern (für eine sog. d
-Funktion ¥ viele). Das heißt, bei einem solchen scharfen Wellenpaket weiß
ich leider fast nichts mehr über seinen Wellenvektor k
und damit über den Impuls p = 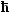 k. Er ist bestenfalls noch bis auf ein Dk
bestimmbar. Rechnet man das durch, erhält man Dx · Dk
> h als grundsätzliche Eigenschaft aller Wellen – und das sollte
uns bekannt vorkommen! k. Er ist bestenfalls noch bis auf ein Dk
bestimmbar. Rechnet man das durch, erhält man Dx · Dk
> h als grundsätzliche Eigenschaft aller Wellen – und das sollte
uns bekannt vorkommen! |
 |
Wellen können auf Randbedingungen wie "Flötenlänge"
reagieren und dann nur noch diskrete Zustände einnehmen |
|
 |
Das ist eine gute Nachricht! Die Quantisierung kommt in der Regel durch die Randbedingungen
zustande (siehe Übung 2.3-1). Ein akustisches Musikinstrument
(eine Orgelpfeife, eine Violinsaite, eine Tuba, ...) kann halt nicht alle Töne hervorbringen – sondern nur die,
die geometriebedingt passen. |
|
 |
Richtig zu bemerken ist das aber nur in Bereichen, in denen Wellenlänge und Geometrie
die gleiche Größenordung haben. In das "Instrument Hörsaal" passen jede Menge Wellen mit nahezu
beliebigen Wellenlängen, die sehr viel kleiner sind als die Ausdehnung des Raums; von der Quantisierung merkt man dann
nichts mehr. Lärm mit beliebigen Frequenzen ist möglich. In anderen Worten: In der halbwegs makroskopischen Welt
wird man von der Quantisierung bei Teilchenwellen mit sehr kleiner Wellenlänge (Aufgabe 2.3-2
) nicht mehr viel merken – es gilt die klassische Physik als sehr gute Näherung! |
|
 |
An dieser Stelle sieht man, warum die Quantentheorie (fälschlicherweise) als Theorie
"nur" für das sehr Kleine gesehen wurde (und wird): Die Quantisierung ist bei Randbedingungen für "große"
Systeme nicht mehr wahrnehmbar. Sie ist aber trotzdem da, und sie definiert die Zustände, auch wenn die Parameter wie
Energie usw. unmessbar dicht nebeneinander sitzen. |
| |
| |
|
Stay cool, (wo)man! |
| |
|
 |
Man kann jetzt leicht zum Schluss kommen:
- Die Quantentheorie kann man nicht verstehen, sondern allenfalls in Form vom Mathematik nachvollziehen und ausrechnen.
- Die einschlägige Mathematik ist grundsätzlich aufwendiger als bei der klassischen Physik.
|
|
 |
Ja, schon – aber ...
- ... das "Verstehen" dauert ja immer ein Weilchen, wenn man mit etwas völlig Neuem konfrontiert wird.
- ... wir können die aufwendige Mathematik (Hilbertraum, Eigenwertprobleme, Operatoralgebra, ...) weitgehend vermeiden.
- ... es gibt eine Vereinfachung derart, dass man die altbekanten klassischen Formeln und Begriffe (sowie die "Denke")
weiter benutzen darf, vorausgesetzt man hat den einen oder anderen Parameter geeignet umdefiniert.
|
|
 |
Punkt 3 beschreibt, was wir hier weitgehend tun werden. |
 |
Also: Kein Grund zur Panik. Wer z. B. den klassischen,
angetriebenen, harmonische Oszillator mit Reibung beherrscht, braucht keine Angst vor dem zu haben, was kommt! Wir werden
ihn nicht quantenmechanisch angehen! |
© H. Föll (MaWi für ET&IT - Script)