The Driven, Damped, Harmonic Oscillator

	In this module we just recall the essentials of the driven and damped harmonic oscillator - for full details see any textbook of physics, e.g. the Feynman lectures I-21 - I-25.
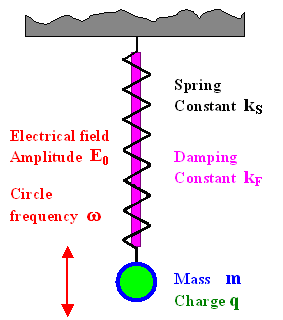
		We are looking at a system that can be visualized as shown .
		We have a mass m hanging on a spring in the gravitational potential of the earth. We assume in addition that the mass is carrying a fixed charge q.
		The system is harmonic, if the force law for he spring is linear, i.e. Hooke's law applies:
		F =  ks · x
		With F = force acting on the spring, x = elongation caused by F, and ks = spring constant.
		In other words: The potential U that m "sees" must be parabolic since we always have F = – dU/dx.
		We also assume that the system is damped, e.g. by a "shock absorber" that is inside the spring like in the suspension system of your car. This is described by damping constant kF ("F" signifies "friction") and makes sure that an oscillation, once started, will not go on forever.
	Finally, we drive the system, i.e. we apply a periodically changing driving force - in this example by an oscillating electrical field characterized by its amplitude E0 and its (circle) frequency w.
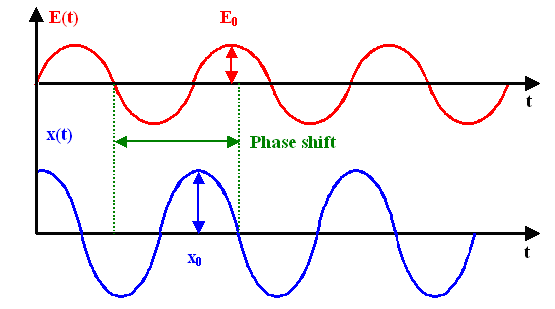
	We are interested in two things, as shown below:
		1. The amplitude x0 of the oscillation as a function of the system parameters, in particular as a function of the frequency of the driving force.
		2. The phase of the oscillation relative to the phase of the driving force.
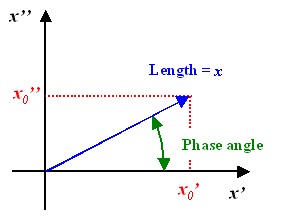
	We can rephrase these questions by describing the amplitude of the oscillations as a sum of two sinus function, one exactly in phase with the driving fore, and the other one shifted by 90o (which simply makes it a cosine function relative to the in-phase sin function)
		In this case we ask for the in-phase amplitude x0' and the out-of-phase amplitude x0''. The total amplitude x0 then follows most easily from the "pointer" diagram as shown on the right, we have (with f = phase angle)
		x  =  æ è x'  +  x'' ö ø 1/2  =   x'' sin f  =  x' cosf
		By now you realize (it is hoped) that this leads up to the complex notation generally employed for periodic phenomena (otherwise read up on complex numbers and pointer diagrams, or use the (German) link).
	Anyway, first we have to write down the differential equation for the system. It follows (almost) straight from Newtonian mechanics, we have
		m · d2x dt2  +  kF · m · d x d t  +  ks · x   =  q · E0 · cos(wt)

	This is simply the force equilibrium and the only non-trivial force in this equation is the term kF · m · dx/dt
		This is the damping or friction term, we simply assume that it is proportional to the mass m and its velocity dx/dt. The proportionality constant is our damping constant kF times the mass.
		Often the friction term is just written as k*F · dx/dt, i.e. the mass is included in k*F, but our approach has a certain advantage as we will see below.
		While all other terms come from ironclad first principle physical law (always assuming harmonic potentials), the friction term is a bit arbitrary; its exact formulation depends on the specific problem.
		However, if you have a system where the amplitude "decays" exponentially after the driving force is switched off, you must have a damping term as given. Essentially you are back to the very general model of relaxation into the ground state as employed for the frequency dependence of the orientation polarization.
	We are now stuck with solving a linear second order differential equation - and we know how that is done.
		Usually, we would move step by step, first looking at a simplified system without damping and driving forces, and then adding the complications.
		What we would find for the simplified system is that there is a special frequency w0 called the resonance frequency or "Eigenfrequency", which is the simply the frequency with which the system will oscillate by itself if started once. The resonance frequency without damping we call w0'; it is given by
		w0'  =  æ ç è kS m  ö ÷ ø 1/2
		With damping added, the resonance frequency changes somewhat, and the amplitude will decrease with time after some initial push started an oscillation. This is described by the following equations
		x(t)  =  x0 · cos(w0t) · exp –   kF 2   · t w0  =  æ ç è kS  m   –  kF2 4  ö ÷ ø 1/2
	If, for a moment, we apply these equations to an ion sitting in a lattice, we will notice two interesting points:
	1. The "spring constant" follows from the binding potential. It is - of course - related to Youngs modulus Y which tells us how much the length of a specimen changes under an applied force, or more precisely, how stress applied to a material creates (elastic) strain. For a homogeneous isotropic material we actually have
		kS  = Y  · a0
		With a0 = bond length » lattice constant. In other words, we know a lot about the spring constant for the systems we are treating here.
		What that means is that we also have a good idea for the order of magnitude of the resonance frequency. It will come out to be roughly 1013 Hz.
	2. The damping or friction constant kF for a single atom, which is coupled by "bond springs" to some other atoms, which are coupled by bond springs ... and so on, is far more difficult to assess. Off hand, most of us probably do not have the faintest idea about a possible numerical value, or if kF relates somehow to some quantities we already know, like the spring constant.
		However, realizing that the dimension of the damping constant is [kF] = 1/s, and that it takes just a few reciprocal kF's before the oscillation dies out, we can make an educated guess:
		If you "snap" just one atom of a huge collection of more or less identical atoms, all connected by more or less identical springs, pretty soon all atoms will oscillate. And the original energy, initially contained in the amplitude of the "snapped" atom, is now spread out over all atoms - which means that their amplitudes will be far smaller than the original one. To get the idea, just look at the picture.
		In other words: There is no doubt that it will just take a few - say 5 or maybe 50 - oscillations of the primary atom, before the orderly energy contained in the oscillation of that one atom will have spread and became diluted and disordered.
		In yet other words: excess energy contained in the oscillations of one atom will turn into thermal energy (= random vibrations of all the atoms); it becomes thermalized rather quickly - in the time it takes to oscillate back and forth a few times.
		kFw is thus tied to w0, we expect it to be very roughly in the order of 5w0 .... 50w0.
	So far so good. But now we must go all the way and switch on "driving", in our example an electrical field that pulls at the charged mass with a force that oscillates with some arbitrary frequency w
		However, we will not even try to write down the solution the full differential equation given above in "straight" terms - it is too complicated, and there is a better way. We will, however, consider the solution qualitatively.
		We (should) know that the mass oscillates with the frequency of the driving force and an amplitude that depends on the frequency (and the damping constant and so on), and that there will be a phase shift between the driving force and the oscillating mass that also depends on the frequency, and so on.
		We also (should) know what all of this looks like - qualitatively. Here it is:
	What we are going to do, of course, is to describe the driven damped harmonic oscillator in complex notation. The basic equation than is
		m · d2x dt2  +  kF · m · d x d t  +  ks · x   =  q · E0 · exp(iwt)
	The solutions are most easily obtained for the in-phase amplitude x0' and the out-of-phase amplitude x0''.
		The total amplitude x0 and the phase shift f are contained in these amplitudes. If we want to have them, we simply calculate them as outlined above.
	The solution we will obtain is
		x(w, t)   =   x(w) · exp (iwt) x(w)  =   q · E0 m æ ç è æ è w02 – w2 (w02 – w2)2 + kF2 w2 ö ø   –  i · æ è kF w (w02 – w2)2 + kF2 w2 ö ø ö ÷ ø   x'(w)  =   q · E0 m æ ç è w02 – w2 (w02 – w2)2 + kF2 w2 ö ÷ ø   x''(w)  =   q · E0 m æ ç è kF w (w02 – w2)2 + kF2 w2 ö ÷ ø
		This looks complicated, but is, in fact, far more elegant than the description without complex numbers. If we plot x'(w) and x''(w), we obtain the following curves
	These curves are purely qualitative. A quantitative rendering can be obtained by the JAVA module below
		Instead of the spring constant, you may enter Youngs modulus directly. Typical numbers (in GPa) are: Diamond: 1000 Carbides, Oxides, Nitrides: » 300 - 600 Glas: 70 Quartz: 100 Alkali halides: 15 - 70 Wood: 10 Polymers: 1 - 10 Rubber: 0.001 - 0.1
		The damping constant enters with its reciprocal value normalized to w, i.e. roughly the number of cycles it takes to dampen out an oscillation.
		You can compare two sets of parameters, because the last curve will always be shown with the new curve.
		You can also enlarge any portion of the diagram by simply drawing a window on the part you like to see enlarged.

With frame

3.3.3 Resonance for Ionic and Atomic Polarization

Solution to 3.2-3

© H. Föll (Electronic Materials - Script)