3.2.3 Ionic Polarization

Consider a simple ionic crystal, e.g. NaCl.

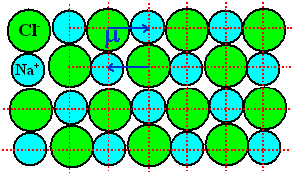
The lattice can be considered to consist of Na⁺ - Cl^– dipoles as shown below.

Each Na⁺ - Cl^– pair is a natural dipole, no matter how you pair up two atoms.

The polarization of a given volume, however, is exactly zero because for every dipole moment there is a neighboring one with exactly the same magnitude, but opposite sign.

Note that the dipoles can not rotate; their direction is fixed.

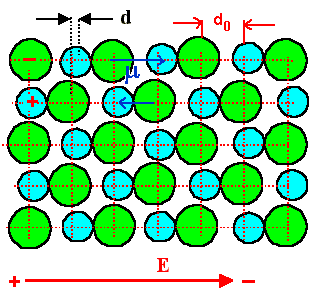
In an electric field, the ions feel forces in opposite directions. For a field acting as shown, the lattice distorts a little bit (hugely exaggerated in the drawing)

The Na⁺ ions moved a bit to the right, the Cl^– ions to the left.

The dipole moments between adjacent NaCl - pairs in field direction are now different and there is a net dipole moment in a finite volume now.

From the picture it can be seen that it is sufficient to consider one dipole in field direction. We have the following situation:

Shown is the situation where the distance between the ions increases by d; the symmetrical situation, where the distance decreases by d, is obvious.

How large is d? That is easy to calculate:

The force F₁ increasing the distance is given by

F₁ = q · E

With q = net charge of the ion.

The restoring force F₂ comes from the binding force, it is given as the derivative of the binding potential. Assuming a linear relation between binding force and deviation from the equilibrium distance d₀, which is a good approximation for d << d₀, we can write

F₂ = k_IP · d

With k_IP being the "spring constant" of the bond. k_IP can be calculated from the bond structure, it may also be expressed in terms of other constants that are directly related to the shape of the interatomic potential, e.g. the modulus of elasticity or Youngs modulus.

If we do that we simply find

k_IP = Y · d₀

With Y = Youngs Modulus, and d₀ = equilibrium distance between atoms.

From force equilibrium. i.e. F₁ – F₂ = 0, we immediately obtain the following relations:

Equilibrium distance d

d =	q · E Y · d₀

Induced dipole moment m (on top of the existing one)

m =	q² · E Y · d₀

Polarization P

P =	N · q ² · E Y · d₀

Of course, this is only a very rough approximation for an idealized material and just for the case of increasing the distance. Adding up the various moments - some larger, some smaller - will introduce a factor 2 or so; but here we only go for the principle.

For real ionic crystals we also may have to consider:

More complicated geometries (e.g. CaF₂, with ions carrying different amount of charge).

This example was deliberatly chosen: The dielectric constant of CaF₂ is of paramount interest to the semiconductor industry of the 21st century, because CaF₂ is pretty much the only usable material with an index of refraction n (which is directly tied to the DK via e_r = n²) that can be used for making lenses for lithography machines enabling dimensions of about 0,1 mm.

If the field is not parallel to a major axis of the crystal (this is automatically the case in polycrystals), you have to look at the components of m in the field direction and average over the ensemble.

Still, the basic effects is the same and ionic polarization can lead to respectable dielectric constants e_r or susceptibilities c.

Some values are given in the link.

Questionaire
Multiple Choice questions to 3.2.3