|
Für alle Rechnungen sieht das Schema so aus:
- " Input" ist das Potential U(r).
- "Output" ist die komplexe Wellenfunktion
y(r) plus die zugehörige Gesamtenergie
E.
- Die Verknüpfung von Input und Output leistet die Schrödingergleichung,
rechts in Kurzform notiert (mit dem Skalarprodukt
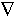 · ·
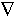 = Summe der zweiten partiellen Ableitungen nach allen drei Ortskoordinaten). = Summe der zweiten partiellen Ableitungen nach allen drei Ortskoordinaten).
- Das Betragsquadrat
y · y* · dV gibt die Wahrscheinlichkeit
an, das behandelte Teilchen im Volumenelement dV zu finden.
|
|
| – |
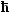 2 2
2m |
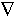 · · 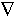 y y |
+ (U – E)y |
= 0 |
|
|
| |
| |
|
 |
Im allgemeinen gibt es viele (meist ¥
viele) Lösungen, die mit Quantenzahlen n, m, ... durchnumeriert werden. |
|
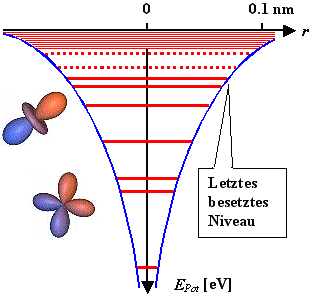 |
| Die Ionisierungsenergie I ist im Bild enthalten! (Die Energieachse muß natürlich
nach oben zeigen.) |
|
|
 |
Eine der Lösungen = ein
möglicher Zustand des Systems. |
|
|
 |
Zu jedem Zustand yn, m, ... gehört eine
Energie En, m, ... | |
|
 |
Verschiedene Zustäden können dieselbe Energie
haben. Die Energie ist dann bezüglich der zustandsbeschreibenden Quantenzahlen entartet. |
|
 |
Was man erhält, z. B. für ein Atom, kann wieder in einem Potentialtopfmodell
visualisiert werden Þ |
|
|
 |
Gezeigt sind zwei Wellenfunktionen = 2 Zustände mit zugehörigen E-Werten
und weitere Energieniveaus ohne Wellenfunktionsbild. | |
|
 |
Welche Lösungen realisiert werden (= welche Zustände mit
Elektronen besetzt werden), entscheidet - die Natur der betrachteten Teilchen sowie
- die "Temperatur" oder die Einbettung in die "Umwelt" (in der Regel das Prinzip der Minimierung der
Energie).
| |
| | |
| |
 |
Alle Teilchen haben auch Welleneigenschaften und können interferieren, im
Extremfall mit sich selber (Doppelschlitzexperiment). | |
| p | = |
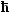 k k | | l | = |
2p
|k| |
|
|
|
 |
Entscheidende Größen sind die Wellenlänge l,
der Wellenvektor k und der Impuls p . |
|
|
 |
Sie sind durch die de Broglie-Beziehung
gekoppelt. | |
| | |
| |
 |
Es gibt zwei fundamentale Teilchensorten:
- Bosonen; mit ganzzahligem Spin
(s = 0, ±1, ±2, ...); z. B. Photonen: s = ±1
- Fermionen; mit halbzahligem Spin (s = ±½,
±3/2, ...); z. B. Elektronen, Protonen, Neutronen: s = ±½
|
|
Elektronen in einem
System können
nie
denselben Zustand einnehmen |
|
|
 |
Für Fermionen (und nur für Fermionen) gilt das
unglaublich wichtige Pauli-Prinzip Þ |
|
|
| |
| |
 |
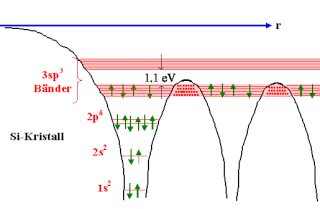
Wichtig ist, was passiert, wenn man aus einzelnen Potentialtöpfen für
Elektronen einen Kristall macht – durch Überlappung der Einzeltöpfe. |
|
|
|
 |
Das Pauli-Prinzip erzwingt die Aufspaltung von überlappenden
Einzelniveaus in Bänder (bei gleichzeitiger Energieabsenkung; sonst tritt keine
Bindung auf). | |
|
 |
Wie diese Bänder genau aussehen, d.h. wieviele Plätze (= Zustände) sie Elektronen
bei der Energie E bieten, entscheidet über die wesentlichen elektronischen Eigenschaften
des Materials (Leiter, Halbleiter, Isolator, ...). | |
| | |
| |
 |
Aufgaben: | |
|
|
 |
Diese beiden Aufgaben sind sehr lehrreich. Þ
Man sollte sie zumindest nachvollziehen! | |
|
|
| |
| |
| |
| |
|
| |
|
 |
Hier noch ein "Multiple Choice"-Test, der zwar etwas über den Stoff
hinausgeht, aber man kann es ja mal probieren! | |
| | |
|
|
|
| |
|
| |
| |
© H. Föll (MaWi für ET&IT - Script)
 ·
·
 = Summe der zweiten partiellen Ableitungen nach allen drei Ortskoordinaten).
= Summe der zweiten partiellen Ableitungen nach allen drei Ortskoordinaten).