 |
1. Zeige, dass die allgemeine eindimensionale Lösung (unter Benutzung
der Normierungsbedingung) die folgende Form hat: |
 |
Wir starten mit zweimaliger Differentiation der zu verifizierenden Lösung in einer Dimension.
Wir erhalten |
| |
| y(x) | = |
æ
ç
è |
1
L |
ö
÷
ø | 1/2 |
· exp | (i · k · x) |
|
dy
dx |
= | æ
ç
è
| 1
L |
ö
÷
ø | 1/2 |
· i · k · exp | (i · k · x)
| |
d2 y
dx2 |
= | æ
ç
è
| 1
L |
ö
÷
ø | 1/2 |
· (– 1) · k2 · exp |
(i · k · x) |
|
|
|
 |
Eingesetzt in die Schrödingergleichung und mit (1/L) 1/2 = L* (um Schreibarbeit
zu sparen), ergibt sich im Gebiet mit U = 0 eV |
|
|
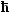 2 2
2me | · |
L* · k2 · exp(i · k · x) |
= |
E · L* · exp(i · k · x) |
|
|
 |
Unser Lösungsansatz ist also dann, und nur dann eine
Lösung, falls folgende Bedingung erfüllt ist: |
|
|
| E | = |
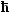 2 · k2 2 · k2
2me |
|
|
|
 |
Das ist die postulierte Gleichung für die Gesamtenergie; der erste Teil der Aufgabe ist
damit erledigt. |
|
 |
Die Normierungsbedingung schenken wir uns hier; sie kommt gleich noch dreidimensional. |
 |
2. Zeige, daß wir damit auch die dreidimensionale
Lösung für einen Kristall der Ausdehnung Lx = Ly = Lz
= L haben (unter Benutzung der dreidimensionalen Normierungsbedingung),
in der Form |
|
 |
Die dreidimensionale Schrödingergleichung kann wegen des gegebenen Potentials durch einen Produktansatz
der Form y(r) = y1(x) · y2(y ) · y3(z) gelöst werden.
|
|
 |
Was für die x-Richtung galt, gilt auch für die y- und z-Richtung,
also für die Komponenten eines Ortsvektors r = (x, y, z) und eines Vektors
k = (kx, ky, kz), der notwendigerweise die Dimension
[1/cm] hat und den wir Wellenvektor nennen. |
|
 |
Wir haben also |
| |
| y(r) | = |
L** | · exp |
(i · k · r) |
|
|
|
 |
Der Vorfaktor L** muss jetzt aus der dreidimensionalen
Normierungsbedingng bestimmt werden: |
| |
L
ó
õ
0 |
L
ó
õ
0 |
L
ó
õ
0 |
(L**)2 · exp(i · k · x) · exp(– i · k
· x) · dxdydz != 1 |
= (L**)2 · | L
ó
õ
0 | L
ó
õ
0 | L
ó
õ
0 |
dxdydz |
|
|
|
 |
Das Integral ist natürlich schlicht = L3; wir erhalten |
| |
| L3 · (L**)2 | = 1 |
| L** = |
æ
ç
è |
1
L |
ö
÷
ø |
3/2 |
q.e.d. |
|
|
 |
Wir sehen auch, wo die lästigen Potenzen 3/2 etc. herkommen, die fast jede Formel
der Quantentheorie verunstalten: |
|
 |
Die 2 kommt von der immer erforderlichen Quadrierung der Vorfaktoren bei der Betragsquadratbildung
der Wellenfunktion, und die 3 oder was immer von den Dimensionen des betrachteten Problems. |
|
 |
Lästig, unschön, zu Fehlern verführend - aber eigentlich trivial. |
| | |
 |
3. Zeige, daß die unten angeführten Gleichungen für
den Wellenvektor
k sich aus der (periodischen) Randbedingung y (r + L)
= y(r) ergibt. |
 |
Für den dritten Teil müssen wir die Randbedingungen in die Lösung einsetzen,
d.h. |
| |
| L* · exp(i · kx · x) |
= |
L* · exp[i · kx · (x + L)] |
| | |
| = |
L* · exp(i · kx · x) · exp(i ·
kx · L) |
|
|
 |
Die Gleichungen für ky und kz
sind natürlich entsprechend. Diese Gleichungen können nur befriedigt werden, falls gilt |
| |
| L* · exp(i · kx, y, z · L) |
= | 1 |
| | |
|
| kx, y, z | = |
nx, y, z · |
2p
L | |
| | |
| |
| nx, y, z | = |
0, ±1, ±2, ±3, .... |
|
|
 |
Die Quantenzahlen, die unsere Lösungsmannigfaltigkeit
sortieren, kommen also aus den Randbedingungen! |
|
|
 |
4. Jetzt zu den schwierigen Fragen: |
 |
Was bedeutet diese Lösung für Elektronen im "Kristall"
anschaulich? |
 |
Ein Ausdruck der Form
A = A0 · expi(kr) beschreibt grundsätzlich eine ebene
Welle, die in k-Richtung mit der Wellenlänge l= 2p/|k|.
Damit die Welle "läuft", multipliziert man noch mit dem Phasenfaktor
exp(iwt). Unbedingt
nachlesen! |
|
 |
Was "wellt" ist y, die dimensionslose
Wellenfunktion. Was das bedeutet erschließt sich erst, wenn man aus der Wellenfuntion meßbare Parameter ableitet. |
|
 |
Die möglichen Richtungen im Kristall, in denen es "wellen" darf, sind durch
die gequantelten Werte für k vorgegeben. |
 |
Wo befindet sich das Elektron eigentlich? |
|
 |
Das ist einfach: Die Aufenthaltswahrscheinlichkeitsdichte
W ist |
| |
|
W = y(r) · y*( r ) |
= | æ
ç
è
| 1
L |
ö
÷
ø | 3 |
· exp | (i · k · r) |
· exp | –(i · k · r) |
= | æ
ç
è
| 1
L |
ö
÷
ø |
3 |
|
|
|
 |
Die Wahrscheinlickeit, das Elektron irgendwo im Kristall zu finden ist überall gleich
groß! Es "gehört" damit dem ganzen Kristall und hat sich "gleichmäßig verteilt". |
 |
Wo sind die Energieniveaus in diesem rechteckigen Potentialtopf? Die ersten
10 oder so kann man ja leicht ausrechnen und einzeichnen. |
|
 |
Das macht jetzt Arbeit. Am besten wir machen eine Tabelle und schauen mal, was wir für größer
werdende Quantenzahlen nx, y, z so bekommen: |
|
|
| Quantenzustand |
Energie
(× Konstante ) |
Zustände |
Zahl der e–
pro E
| | nx |
ny |
nz |
| 0 | 0 | 0 |
0 |
|
1 | 2 |
±1
0
0 | 0
±1
0 |
0
0
±1 |
1 |
2
2
2 |
6 |
12 | ±1
±1
0
| ±1
0
±1 |
0
±1
±1 |
2 |
4
4
4 |
12 |
24 | | ±1 |
±1 | ±1 |
3 | |
8 | 16 |
±2
0
0 | 0
±2
0 |
0
0
±2 |
4 |
2
2
2 |
6 |
12 |
| Weiter ohne Details | | 2
| 1 | 0 |
5 | |
| 48 |
| 2 | 1 | 1 |
6 | |
| ? |
| 2 | 2 | 0 |
8 | |
| ? |
| 2 | 2 | 1 |
9 | |
|
? |
| 3 | 0 | 0 |
| |
und so wie weiter? |
|
|
 |
Damit können wir die Energieniveaus und die Maximalzahl an Elektronen pro Niveau (= Entartungsgrad)
für kleine Quantenzahlen mal einzeichnen: |
|
|
|
|
 |
Schon merkwürdig. Ein einfach erkennbares Bildungsgesetz gibt es nicht - es fehlt z. B. das Energieniveau
bei "7"; vom Entartungsgrad mal ganz zu schweigen.
Daran werden wir noch arbeiten müssen! |
 |
Was passiert, falls wir mehr als ein Elektron betrachten? |
|
 |
Immer dieselbe Leier. Wir betrachten immer nur das "letzte", alle anderen schlagen wir gemittelt
dem Grundpotential zu. Damit bleibt die Struktur der Lösung erhalten, während Zahlenwerte sich vielleicht ändern. |
|
 |
Wir haben weiterhin diskrete Niveaus mit irgendeinem Entartungsgrad, und diese Niveaus füllen wir
"von unten her kommend" mit Elektronen auf, bis das letzte untergerbracht ist. |
|
 |
Falls es jemand nicht gemerkt haben sollte: Wir haben hier erstmalig in primitiver Form die
bereits postulierten Energiebänder
für die bindenden Elektronen im Kristall ausgerechnet! |
|
| |
© H. Föll (MaWi für ET&IT - Script)
![]() Übung 2.3-2: Wellenlänge von Teilchen
Übung 2.3-2: Wellenlänge von Teilchen