|
In den vorhergehenden Kapiteln haben wir zwei sehr mächtige Prinzipien kennengelernt,
codiert in den simplen Formeln (die man wissen muss!) |
| |
| Si | = |
kB · ln pi | | |
| | | G | = |
U – TS |
|
|
|
 |
Das Rechnen mit diesen Formeln war aber mühsam, dies galt insbesondere für die Entropieformel. |
 |
Nun sind aber Atome und Elektronen nicht besondere intelligent, sie haben, ähnlich
wie Erstsemester oder Banker, von diesen Formeln noch nie etwas gehört – trotzdem kennen sie für jede Situation
die exakte Lösung! Wir stellen uns damit mal die Frage: Was tut so ein Atom oder Elektron
eigentlich , um ein System, das im Gleichgewicht ist, herzustellen? |
|
 |
Die Antwort, schon oft angeklungen, ist einfach: Das Teilchen "besetzt" einen möglichen
Zustand mit einer definierten Energie. Das Wort "besetzt" meint
damit keinesfalls "irgendwo im Raum zu sitzen", also ortsfest zu sein. Das Gasatom, das den Zustand v = (34,
16, -321) m/s besetzt hat, also mit der vektoriellen Geschwindigkeit wie angegeben durch die Gegend fliegt, ist gerade
"irgendwo", aber es "sitzt" fest auf dem Energieniveau E1 = ½
mv2. |
|
 |
Nimmt man die Komponenten des Geschwindigkeitsvektors v = (v x,
vy, vz) als Definition eines Zustandes (wie hier geschehen),
haben alle
Zustände, für die vx2 + vy2 + vz2 = const
gilt, offenbar dieselbe Energie, und damit liegt hier Entartung vor. |
 |
Statt dem Begriff "Entartung
", der vor allem bei diskreten Energieniveaus sinnvoll ist, definieren wir jetzt eine neue Größe, die
Zustandsdichte
D(E ) . Sie bestimmt im Grunde dasselbe wie die Entartung, aber macht das sehr viel eleganter, insbesondere
für sehr dicht benachbarte Energieniveaus oder sogar für Energiekontinua. |
|
 |
Wir definieren einfach für die (differentiell kleine) Zahl der Zustände dN(E)
in einem Energieintervall dE |
| |
| dN(E ) = D(E) · dE = |
Zahl der Zustände im
Energieintervall von E bis E + dE |
pro cm3 |
|
|
 |
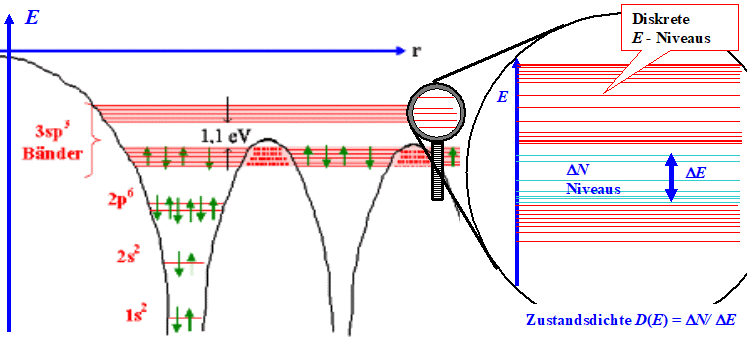
Hier ist das Bild dazu – bezogen auf das schon bekannte
Bild, das die Enststehung der Energiebänder aus den diskreten
Niveaus der Atome beim Silizium zeigt: |
|
|
|
 |
Das ist im Grunde sehr einfach. Die Zustandsdichte mal dE gibt einfach nur die
Zahl oder, genauer gesagt, Volumendichte der verfügbaren
Plätze in einem (kleinen) Energieintervall dE an (D(E) = dN/d
E), die durch die betreffenden Teilchen besetzt werden können, und das auch noch pro cm3.
Wir haben also sowohl eine Dichte bezogen auf die Energie (D(E) = dN/dE) als
auch bezogen auf das Volumen. |
 |
Zu jedem System gibt es eine Zustandsdichte D(E). Wie die
damit beschriebene Funktion genau aussieht, ist von System zu System verschieden. D(E) ist auch nicht
unbedingt eine einfache Funktion. Sie kann sehr kompliziert aussehen; häufig (z.B. für Elektronen in Halbleitern)
ist sie auch sehr kompliziert. Der Link zeigt ein Beispiel. |
|
 |
Aber was soll's – die Zustandsdichte ist für ein gegebenes System oder Material
(z.B. für die Elektronen in Halbleiterkristallen) eine Material"konstante". Hat man sie einmal berechnet
oder gemessen, hat man sie für alle Zeiten. |
 |
Unser Problem kann damit neu formuliert werden: Wir haben ein System (wir denken
jetzt immer an Halbleiter), dessen Zustandsdichte wir kennen. Die einzige Frage, die
man jetzt noch stellen kann, ist: |
|
|
| Wie verteilen sich die Teilchen des Systems im Gleichgewicht auf die vorhandenen Zustände
und damit Energien? |
|
|
 |
Haben wir die Antwort einmal gefunden, gilt sie für alle Zeiten, denn im Gleichgewicht
ändert sich (im Mittel) per definitionem nichts mehr! |
 |
Die Frage läßt sich auch anders stellen. Wir fragen: |
| |
| Mit welcher Wahrscheinlichkeit w(E) ist im Gleichgewicht ein Platz bei der
Energie E mit einem Teilchen des Systems besetzt? |
|
 |
Die Dichte n(E) (= Zahl Teilchen pro
cm3) der Teilchen mit Energien zwischen E und E + DE
ist dann gegeben durch |
|
|
| n(E) | = |
Zustandsdichte mal
Wahrscheinlichkeit der Besetzung mal
Energieintervall |
| | | | | = |
D(E) · w(E) · DE |
|
|
| |
Das ist eine im Prinzip einfache, aber ungeheuer wichtige Beziehung,
die wir noch oft brauchen werden!
|
|
| |
|
 |
Jetzt aber zu den guten Nachrichten: |
 |
1. gute Nachricht: Mit nur zwei
Verteilungsfunktionen
w(E) kann man alle
Systeme auf der Welt (und im gesamten Universum) beschreiben! |
|
 |
Wir brauchen zwei Verteilungsfunktionen, denn wir haben
zwei grundverschiedene Teilchensorten: Die Bosonen
und die Fermionen
! Jetzt sollte man unbedingt noch mal nachschauen , worin
der fundamentale Unterschied zwischen den beiden Arten besteht! Wir fassen schnell zusammen:
- Auf einem Zustand kann immer nur ein Fermion (z.B. ein Elektron) sitzen.
- Auf einem Zustand können beliebig viele Bosonen oder klassische Teilchen sitzen.
|
|
 |
Dieser fundamentale Unterschied in den Möglichkeiten, sich auf gegeben Energiplätze
zu verteilen, spiegelt sich in der zugehörigen Verteilungsfunktion wider; es gibt also zwei
davon. |
 |
2. gute Nachricht: Falls die Teilchen eines gegebenen Systems auf die verfügbaren
Plätze (gegeben durch die Zustandsdichte des betreffenden Systems) nach Maßgabe der zuständigen Verteilungsfunktion
aufgeteilt sind, ist das System immer und "automatisch" im Minimum seiner freien Energie
(und damit im Gleichgewicht). |
|
 |
Wenn das mal keine gute Nachricht ist! Nie mehr Kombinatorik mit Fakultäten usw., um
Entropien auszurechnen. Aber halt! Haben wir uns statt der Pest jetzt die Cholera eingehandelt? Sind die beiden Verteilungsfunktionen
möglicherweise wahnsinnig kompliziert? Sind sie nicht! |
 |
3. gute Nachricht:Die beiden Verteilungsfunktionen für Fermionen bzw.
Bosonen sind mathematisch so einfach, wie es gerade noch geht, um die benötigte Funktionalität darstellen zu können. |
 |
4. gute Nachricht: Oft, d. h. unter Umständen, die wir noch genauer
anschauen werden, kann man diese beiden Verteilungsfunktionen in sehr guter Näherung durch eine
einzige mathematisch noch einfachere Verteilungsfunktion beschreiben, nämlich der für klassische
Teilchen – und das ist die Boltzmann-Verteilung, die wir etwas weiter unten
ausführlich einführen. |
|
 |
Klassische Teilchen gibt es "eigentlich"
ja gar nicht. Mit dem hier gegebenen Hintergrund können wir sie aber sehr einfach definieren: |
| |
"Klassische" Teilchen sind Bosonen oder Fermionen unter Umständen,
bei
denen die
Boltzmann-Verteilung
zur näherungsweisen Beschreibung vollkommen ausreicht. |
|
 |
Es wird jetzt Zeit, diese Verteilungsfunktionen so weit als erforderlich zu konkretisieren. |
|
|
|
Die Boltzmann-Verteilung für klassische
Teilchen |
| |
|
 |
Die Überschrift sagt es schon: Klassische Teilchen gehorchen der Boltzmann-Verteilung , der
wir im übrigen schon mehrfach begegnet sind. |
|
 |
Hier ist der entsprechende Teil aus dem Kapitel "4.2.2
Diffusion mit atomaren Fehlstellen und Ficksche Gesetze": |
| |
| Falls ein "thermodynamisches System" |
| wie ein Kristall |
verschiedene angeregte Energiezustände E i
| | |
| relativ zum Grundzustand E0 hat |
| |
| (mit E0 = Zustand mit der kleinsten Energie),
| |
:= 0 = alle Plätze mit Atomen besetzt
| | dann ist im thermodynamischen Gleichgewicht |
| |
| die Zahl der "Teilchen" Ni |
| wie z.B. Leerstellen
= Atome "weg" |
| bei der Energie Ei |
|
= Bildungsenergie EF |
| gegeben durch | |
|
|
Ni
N0 |
= exp ( – |
Ei
kB T
| ) |
|
|
|
 |
Falls die weitaus überwiegende Zahl der Teilchen auf dem Grundniveau
(per definitionem bei E = 0 eV) sitzt, kann man das noch vereinfachen zu |
| |
| Ni |
= Ntotal · exp ( – |
Ei
kBT |
) |
|
|
|
 |
Mehr braucht eigentlich nicht gesagt zu werden. Einige Beispiele haben wir im Vorgriff auf
die grundlegende Thermodynamik, die wir hier kurz anschauen, schon behandelt, nämlich Weitere Beispiele werden folgen! |
 |
Da wir die Verteilungsfunktion für Bosonen
(die sog. Bose-Einstein-Verteilungsfunktion
) nicht brauchen werden, lassen wir sie einfach weg. |
|
 |
Damit bleibt nur noch, die Verteilungsfunktion für Fermionen
zu bestimmen, die wir unbedingt brauchen werden. Das werden wir im nächsten Unterkapitel tun. |
© H. Föll (MaWi für ET&IT - Script)