5.3.2 Die Fermi-Dirac-Verteilung

Die Grundlagen zur "Ableitung" der Fermi-Dirac-Statistik

	Was genau ist die Frage? Als ET&IT-Studis wollen wir in erster Linie wissen, wie sich die Elektronen der Halbleiterkristalle auf die Energiebänder verteilen, die wir immer bekommen, wenn wir aus einzelnen Atomen einen Kristall machen.
		Dazu sollte man sich vielleicht nochmal das betreffende Potentialbild anschauen.
	Als Einstieg in die Thematik betrachten wir ein Modellsystem mit konstanter Zustandsdichte. Wir geben 10 Plätze pro eV über den ganzen Energiebereich vor (d.h. D = 10 eV–1 (wir schenken uns das m–3 in der Dimension). In dieses System stecken wir 90 Elektronen. Wir könnten auch D = 10 11 eV–1 und 1012 Elektronen (oder jede beliebige ander sinnvolle Kombination) nehmen, aber das muss dann jemand anders zeichnen.
		Also immer wieder: Prinzipzeichnungen nicht mit der "Realität" verwechseln!
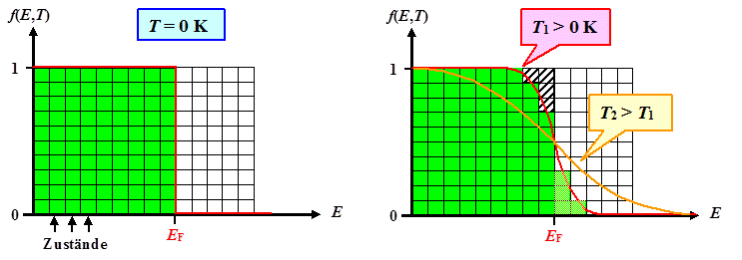
		Wir schau'n dann mal, was bei T = 0 K und T > 0 K in unserem System passiert.
		In jedem Zustand, gekennzeichnet durch eine Energie E, kann man also maximal 10 Elektronen unterbringen. In Diagramm entspricht ein Platz für ein Elektron damit einem Kästchen.
	Die Verteilung der Elektronen auf die Zustände bei T = 0 K ist klar.
		Für ein Minimum der freien Energie G ist jetzt nur die Energie zu minimieren, da in G = E – TS der Entropieterm = 0 ist. Das machen wir, indem wir erst mal alle Plätze bei der niedrigsten Energie besetzen, dann alle Plätze bei der zweitniedrigsten Energie usw, bis wir alle 90 Elektronen energiegünstigst untergebracht haben - so wie oben links gezeigt.
		Bei irgendeiner Energie sitzt das "letzte" Elektron. Dieser Energie geben wir einen Namen, sie heißt ab sofort Fermienergie EF. Auch das kam schon mal vor. Per definitionem sind bei T = 0 K alle Zustände bis zur Fermienergie besetzt; danach ist alles leer.
		Für ein gegebenes System (d.h. wir kennen die Zustandsdichte und die Zahl der Teilchen), z. B. ein Stück Si-Kristall, liegt die Fermienergie damit fest, man kann sie als einen Materialparameter betrachten.
	Jetzt schauen wir uns mal an, wie ordentlich oder unordentlich wir die Elektronen verteilt haben.
		Insgesamt gibt es offenbar genau eine Möglichkeit, alle 90 Elektronen unterhalb der Fermienergie unterzubringen.
		Wir haben also größtmögliche Ordnung erzeugt, da wir nur einen Mikrozustand haben, um die gewünschte Anordung mit minimaler Energie zu realisieren. Das ist gleichbedeutend mit einem Zustand minimaler Entropie. Bei T = 0 K ist das ja auch "in Ordnung".
	Jetzt machen wir mal das gleiche Spielchen bei einer endlichen Temperatur T1. Dann liegt aber im Minimum der freien Energie etwas Unordnung vor - bei möglichst minimaler Energieerhöhung.
		"Unordnung" bedeutet hier, aus einem besetzten Energieniveau einige Elektronen herauszunehmen und diese (ungern, aber notgedrungen) auf bisher unbesetzten Niveaus bei höheren Energien unterzubringen. Das schafft insofern Unordnung, da wir jetzt mehr als eine Möglichkeit haben, um z. B. 8 bzw. 2 Elektronen auf den verfügbaren 10 Plätzen (bei einer bestimmten Energie) unterzubringen.
		Es ist klar, daß wir das Herausnehmen bei den höchsten besetzten Energieniveaus machen und die freigesetzten Elektronen auf die niedrigsten unbesetzten Niveaus bringen - das minmiert den Energie"preis" für die Transaktion. Qualitativ wird das so aussehen, wie mit der roten Kurve gezeigt - wir haben insgesamt vier Elektronen umgeordnet.
		Die orangefarbene Kurve zeigt das Ganze bei noch höherer höherer Temperatur und deshalb mit noch mehr Unordnung. Offenbar wird die Einhüllkurve (= unsere gesuchte Verteilungsfunktion) mit steigender Temperatur immer "weicher".
		Dass wir jetzt zunehmend Unordnung erzeugen, ist auch klar. Die Elektronen um die Fermienergie herum sind nicht mehr ordentlich aufgeräumt; je weicher die Einhüllkurve = Verteilungsfunktion um die Fermieenergie herum wird, desto mehr Unordnung wird erzeugt.
	Das war's dann auch schon. Die im Bild oben gezeigten rote / orangefarbene Kurven stellen ganz offensichtlich die gesuchte Verteilungsfunktion dar. Diese Verteilungsfunktion nennen wir Fermi-Dirac-Verteilung oder in Kurzform schlicht Fermi-Verteilung.
		Wir haben aber ein kleines Problem, erkennbar wenn wir das Bild rechts betrachten: Bei T = 0 K ist die Fermiverteilung unstetig; sie macht einen Sprung von w(E <  EF) = 1 auf w(E  > EF) = 0 . Bei höheren Temperaturen macht sie den Übergang stetig wie gezeigt.
		Welche mathematische Funktion w(E; EF , T) kann das leisten? Wiederum ist die echte Variable die Energie E; EF und T sind Systemparameter. Noch genauer gesagt, ist eigentlich E – EF die Variable, denn es kommt immer nur dieser Ausdruck vor.
		Ein bißchen komplizierter als die Boltzmannverteilung ist die Fermiverteilung wohl schon. Da sie fundamental ist, bezeichnen wir sie auch nicht mehr mit w(E; EF, T) , sondern mit f(E; EF, T). Aber genug des Vorspiels: Die Fermiverteilung ist wie folgt definiert:
		f(E ; EF, T)  =  1  exp æ è E  –  EF kBT ö ø + 1

		Keine beliebig einfache Funktion, aber die einfachste, die das tut, was nötig ist! Man muss diese Formel nicht unbedingt auswendig können, man muss sie aber auf jeden Fall qualitativ zeichnen können!
	Wir machen das ganze nicht zum Spaß: Fermiverteilung und Fermienergie sind fundamental für Halbleiterbauelemente, wir werden uns deshalb die Eigenschaften der Fermiverteilung in nächsten Unterkapitel auch noch etwas genauer anschauen.
	Hier sind die schnellen Fragen:
		Fragebogen Schnelle Fragen zu 5.1.2

© H. Föll (MaWi für ET&IT - Script)