|
Zunächst betrachten wir das Grenzverhalten für T
® 0 K. Das sollte beim Überschreiten der Fermienergie eine abrupte Stufe von 1
auf 0 ergeben. |
|
 |
Wir bekommen in einer Fallunterschiedung: |
| |
| für E – EF
= DE < 0 : | |
f(E, 0K) = |
1
exp (– ¥ ) + 1 |
= 1 | | | | |
| |
| für E – EF = D
E > 0 : | |
f(E, 0K) = |
1
exp (+ ¥) + 1 |
= 0 |
|
|
|
 |
Das ist genau das, was wir brauchen. |
 |
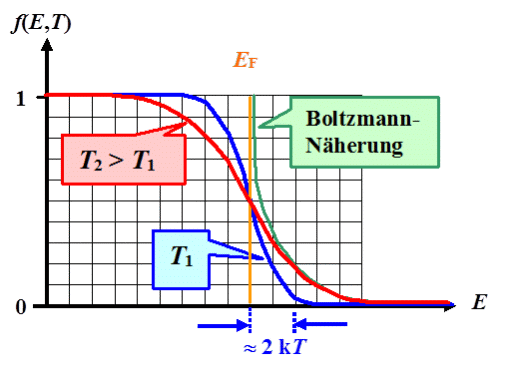
Es ist nun verhältnismäßig einfach, die Fermiverteilung für
eine gegebene Temperatur und Fermienergie auszurechnen. Man erhält Kurven wie folgt: |
| |
|
|
 |
Das Rechteck bei T = 0 K bekommt mit steigender Temperatur zunehmend
eine weiche Flanke; genau so, wie wir es uns überlegt hatten. |
|
 |
Der "weiche" Bereich oder die "Aufweichungszone"
hat dabei eine Breite von ungefähr 4 kBT. Auch das entspricht der Vorhersage - aber jetzt
können wir es ausrechnen; wir werden das auch in einer Übungsaufgabe tun. |
 |
Eine weitere Eigenschaft wird unmittelbar sichtbar (oder ausrechenbar): |
| |
|
|
 |
Die Fermienergie liegt per definitionem bei der Energie, bei der die Wahrscheinlichkeit, dass die Elektronen
die Plätze dort besetzen, gleich 1/2 ist. Das ist eine viel bessere, weil allgemeinere Definition der Fermienergie , die wir noch oft brauchen werden. Sie ist vollständig kompatibel
mit unserer alten Definition, nur besser. |
 |
Wir können weiterhin vermuten, daß der "Hochenergieschwanz" der Fermiverteilung, also die Wahrscheinlichkeit, dass Plätze
bei E >> EF besetzt sind, durch die Boltzmannverteilung
approximiert werden kann; auch das ist oben eingezeichnet. |
|
 |
Das läßt sich leicht zeigen: Für E – EF
>> kBT gilt in der Tat: |
|
|
| f(E, T) » exp ( |
– | E – EF
kBT | ) |
|
|
|
 |
Das ist die Boltzmannverteilung, nur der Energienullpunkt liegt jetzt bei EF.
Dass diese Beziehung stimmt, wird in der folgenden Übungsaufgabe geprüft. |
| |
|
 |
Zum Schluß noch eine auf den ersten Blick etwas seltsam anmutende Beziehung,
die wir aber noch oft brauchen werden: |
|
 |
Die Wahrscheinlichkeit wh dafür,
daß ein Platz bei der Energie E
nicht mit einem Elektron besetzt ist (wir auf diesem Platz sozusagen ein "Loch " [engl. "hole"] haben), ist gegeben durch |
| |
|
|
 |
Wir schauen uns das noch schnell in einer Graphik an: |
| |
|
 |
Damit haben wir jetzt ein mächtiges Werkzeug, um den elektronisch bedingten
Eigenschaften der Materialien und insbesondere der Halbleiter nachgehen zu können. Denn elektronische
Eigenschaften kommen von dem, was die Elektronen im Kristall so treiben, und die sind
nun mal Fermionen. |
|
 |
Das ist übrigens auch gut so: Falls sie Bosonen wären, hätten wir arge Probleme
(die damit anfangen, dass es uns gar nicht geben würde). |
|
| |
 |
Hier sind die schnellen Fragen: |
| |
|
© H. Föll (MaWi für ET&IT - Script)