|
Alle Systeme sind durch eine Zustandsdichte
D(E) gekennzeichnet | |
| D(E) = |
dN
dE | = |
Differentielle Zahl dN der
Zustände im Energieintervall
[E, E +
dE] pro cm3 |
|
|
|
 |
D(E) wäre für ein diskretes Energieniveau der Entartungsgrad. | |
|
 |
Die Zustandsdichte ist eine "doppelte" Dichte: 1. bezüglich der Energie,
und 2. bezüglich des Volumens (trivial). | |
|
 |
[D] = eV–1 · cm–3 |
|
|
| |
| |
 |
Bei gegebener Zustandsdichte entscheidet nur
die Besetzung der daduch gebenen Energieniveaus darüber was das System "tut". |
|
Wie groß ist die Wahrscheinlichkeit dafür, dass ein Platz bei der Energie E besetzt
ist?
(für gegebene Paramter wie Temperatur T, Teilchengesamtzahl N0,
...) |
|
|
 |
Zum Gleichgewicht, d.h. dem Minimum der freien Energie G = U –
TS, gehört eine bestimmte Besetzungssystematik. |
|
|
 |
Die Grund- und Schlüsselfrage ist: Þ |
|
|
| |
| |
 |
Die Antwort auf diese Frage muss eine Verteilungsfunktion
sein | |
Bose-Einstein-Verteilungsfunktion (für Bosonen):
Es können beliebig viele Teilchen = Bosonen auf einem Platz sitzen
(z.B. alle bei E = 0
eV bei T = 0 K)
Fermi-Dirac-Verteilungsfunktion für Fermionen (z. B. Elektronen):
Es
können maximal 2 Elektronen = Fermionen (Spin rauf und runter) auf einem Platz sitzen
(z.B. nicht alle bei E = 0 eV bei T = 0 K) |
|
|
 |
Es gibt genau zwei Verteilungsfunktionen w(E): |
|
|
 |
eine für Bosonen und eine für Fermionen. |
|
| |
| |
| |
 |
Damit ergibt sich als Haupt- und Grundformel für die Konzentration n(E)
an Teilchen bei der Energie E Þ |
|
| n (E ) | = |
Dichte der Plätze mal
Wahrscheinlichkeit der Besetzung mal
Energieintervall |
| = |
D(E) · w(E) · DE
|
|
|
| | |
| |
|
 |
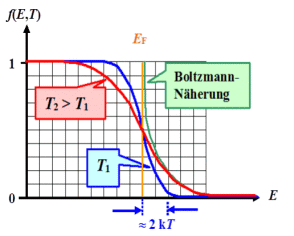
Uns interessiert nur die Fermi-Verteilung: wir nennen sie immer f(E;
EF, T) | |
f(E; EF, T) =
|
1
| | exp |
æ
è |
E – EF
kBT |
ö
ø |
+ 1 |
|
|
|
 |
Wir habe eine Funktion der Energie E mit der Temperatur T und
der Fermienergie EF als Parameter. | |
|
 |
Die Fermienergie ist eine Systemgröße. Sie ist diejenige Energie, bei der die Wahrscheinlichkeit
einer Besetzung = ½ ist. (Bei T = 0 K und einer kontinuierlichen Zustandsdichte
entspricht das der Energie, bei der das letzte Elektron untergebracht werden kann.) |
|
| |
| |
|
| |
|
| | |
| | |
| |
|
 |
Der Graph der Fermiverteilung sieht - leicht erratbar - so aus Þ |
|
|
 |
Die folgende Eigenschafte machen das Arbeiten mit der Fermiverteilung einfach: |
|
|
 |
Die "Aufweichungszone" ist » 4 kBT
breit. | |
|
 |
Für den "Hochenergieschwanz", d. h. für Energien einige kBT
oberhalb der Fermienergie, kann die Boltzmann-Näherung verwendet werden: |
|
|
| |
|
|
|
| f(E,T) » exp |
( – |
E – EF
kBT | ) |
|
| |
|
| |
|
|
 |
Die Boltzmann-Näherung bedeutet immer: Die Teilchen können jetzt "klassisch" beschrieben werden. |
|
|
| |
| |
 |
Die Quintessenz des Ganzen ist: |
| |
| |
| |
|
Die Verteilung von Teilchen auf die verfügbaren
Energieplätzen mit der
Fermiverteilung
oder, in klassischer Näherung,
mit der Boltzmannverteilung , beschreibt immer
den Zustand kleinster freier Energie und damit
thermodynamisches Gleichgewicht
(bei der gegebenen Temperatur T).
|
|
| | |
| |
© H. Föll (MaWi für ET&IT - Script)