|
Als wir uns mit Band-Band-Übergängen
beschäftigt haben, haben wir bereits den Begriff der Ladungsträgerlebensdauer kennengelernt. |
|
 |
Dazu haben wir den Elementarprozeß der Erzeugung oder Generation eines Elektron-Lochpaares, der
anschließenden Thermalisierung und Rekombination angeschaut. |
|
 |
Diese beiden Begriffe sind neben der Dotierung der Schlüssel zur Halbleiterphysik und
-technik. Es schadet nicht, an dieser Stelle die beiden früheren Unterkapitel
noch einmal durchzulesen. |
 |
Wir betrachten jetzt aber dotierte Halbleiter,
d.h. wir haben Minoritäts- und Majoritätsladungsträger mit sehr verschiedenen Konzentrationen, und wir müssen
die Stichworte "Generation", "Rekombination",
"Lebensdauer" und "Diffusionslänge"
unter diesem Aspekt noch einmal betrachten. |
|
 |
Es lohnt sich, für diesen Fall noch einmal den gesamten Zyklus von der
Geburt bis zum Tod eines Ladungsträgers zu betrachten. Wir führen dazu eine Bildbetrachtung durch und interpretieren
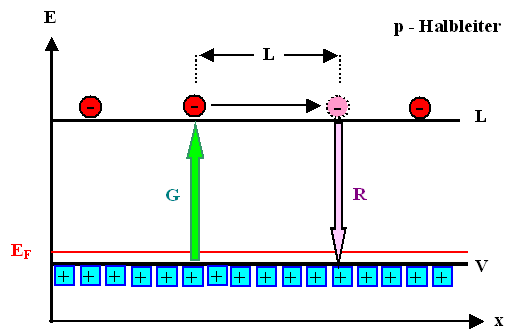
das Banddiagramm des Lebenslaufs einer Minorität in einem p-Typ
Halbleiter. |
| |
|
 |
Aus einer eingehenden Kontemplation dieses Bildes lassen sich folgende Schlußfolgerungen
ziehen: |
|
 |
1. Es enthält redundante Information. Sowohl
die Lage der Fermienergie, als auch die symbolisch eingezeichneten Majoritätsladungsträger "Löcher",
als auch die Beschriftung sagen alle dasselbe: Wir haben einen p-Typ Halbleiter.
|
|
 |
2. Das Verhältnis Majoritäten : Minoritäten ist ungefähr 4 :
1. Damit hätten wir nur eine sehr schwache Dotierung. Es liegt damit nahe, daß der Künstler die Zahl
der Löcher und Elektronen symbolisch meint. Denn ein realistisches Verhältnis
von z.B. 1 000 000 : 1 ist in dieser Kunstform offenbar nicht darstellbar. |
|
 |
3. Im linken Bereich ist ein Generationsereignis
zu sehen. Während der neu erzeugte Minoritätsladungsträger - das Elektron
- eindeutig zu identifizieren ist, bleibt der zugehörige Majoritätsladungsträger "Loch" anonym,
er ist in der Masse der anderen Löcher nicht zu identifizieren. Der Künstler will wohl einen Hinweis darauf geben,
daß sich bei einer leichten Abweichung vom Gleichgewicht bei den Majoritäten
so gut wie nichts ändert, während bei den Minoritäten die Änderungen
deutlich spürbar sind. |
|
 |
4. Im Zentrum des Bildes folgen wir dem Schicksal des frisch generierten Minoritätsladungsträger.
Nachdem er sich eine Länge L von seinem Geburtsort entfernt hat, geht er durch Rekombination wieder ins
Nirwana ein - das Elektron ist (im Leitungsband) spurlos weg. Wiederum fehlt jeder Hinweis auf den Rekombinationspartner
aus der Masse der Löcher. |
|
 |
5. Es läßt sich noch ein letzter Hinweis auf die Vorgänge in und zwischen
den Bändern finden: Alle Minoritäten (und auch die Majoritäten) sind
sich völlig gleich - wir sehen rote Kreise, die für sich genommen völlig ununterscheidbar sind. |
 |
Soviel Information steckt in einem simplen Banddiagramm - man muß sie nur
zu interpretieren wissen! Nüchtern betrachtet nehmen wir jetzt folgende Punkte zur Kenntnis: |
|
 |
1. Ganz offensichtlich ist das, was sich bei den Minoritäten
abspielt, viel wichtiger als die Vorgänge bei den Majoritäten. Denn jede Änderung bei Ladungsträgerkonzentrationen
bewirkt bei den Minoritäten immer sehr viel größere Abweichungen vom Gleichgewicht, als bei den Majoritäten.
Und es sind immer die Abweichung vom Gleichgewicht, die Reaktionen aller Art antreiben! |
|
 |
2. Obwohl wir bisher immer nur einen
Generationsvorgang mit anschließender Rekombination betrachtet haben, muß uns doch klar sein, daß wenn
ein wie auch immer generiertes Elektron nach einer Zeit t
rekombiniert, das dann notwendigerweise für alle Elektronen gelten muß! Denn
alle Elektronen sind gleich und keine sind gleicher! |
|
 |
Damit würden praktisch alle Minoritätsladungsträger
nach ein paar Lebensdauern t verschwunden sein (denn die "Abbaurate" folgt natürlich
dem allgemeinen Gesetz zum Zerfall angeregter Zustände).
Die Rekombinationsrate
R,
d.h. die Zahl der pro Sekunde (und cm –3) rekombinierenden Minoritätsladungsträger, ist
damit einfach |
| |
|
 |
Da aber im Gleichgewicht die Konzentration aller Ladungsträger
konstant sein muß, können wir eine erste, sehr wichtige Schlußfolgerung ziehen: |
|
 |
Im Gleichgewicht muß die Generationsrate
G, d.h.
die Zahl der pro Sekunde (und cm –3) generierten Minoritätsladungsträger genau gleich
groß sein wie die Rekombinationsrate, d.h. |
| |
|
|
 |
Das läßt sich leicht verstehen: Wenn von einem Bankkonto ein bestimmter Betrag
pro Zeiteinheit abgehoben wird - z.B 1 € pro Tag oder 1 000 000 € pro Tag - dann wird der Kontostand
(im Mittel) nur dann konstant bleiben (im Mittel), wenn genausoviel Geld pro Zeiteinheit überwiesen wird. Das hatten wir übrigens schon mal in einem anderen Zusammenhang! |
|
 |
Das Beispiel paßt genau! Und es sagt uns darüberhinaus ganz plastisch, daß
aus der Größe der Ab- und Zuflüsse kein wie auch immer gearteter Schluß auf den Kontostand
gezogen werden kann, wie auch umgekehrt ein wie auch immer gearteter unveränderter Kontostand nichts über die
Höhe der Zu- und Abflüsse aussagt. |
 |
Damit haben wir im (nur so rumliegenden) Halbleiter nicht nur
ein Gleichgewicht, wir haben immer ein dynamisches
Gleichgewicht. |
|
 |
Jeder Minoritätsladungsträger wird irgendwann (und irgendwo) generiert,
läuft (im Mittel) eine Diffusionslänge durch den Kristall, und verschwindet dann wieder durch Rekombination. |
|
 |
Das gilt natürlich im Prinzip auch für die Majoritätsladungsträger. Von
denen ist aber die weitaus überwiegende Anzahl im (dynamischen) Gleichgewicht mit den Dotieratomen
und die paar, die sich mit Minoritäten abgeben, spielen für die Gesamtanzahl keine Rolle. |
| | |
|
Lebensdauer, Diffusionslänge und Beweglichkeit |
| | |
 |
Zum obigen Thema haben wir schon früher (und einige Zeilen weiter oben) schon viel gelernt. Wir wiederholen obige Aussage mal etwas ausführlicher:
|
|
 |
Jeder Minoritätsladungsträger wird generiert, und läuft dann (im Mittel) eine
Diffusionslänge
L durch den Kristall. Dazu braucht er (im Mittel) die Zeit t, die wir ab
jetzt Minoritätsladungsträgerlebensdauer oder kurz Lebensdauer nennen, und verschwindet
dann wieder durch Rekombination. |
|
 |
Der Zusammenhang zwischen Lebensdauer und Diffusionslänge wird dabei
wie bei jedem "Random walk" durch die
folgende Beziehung gegeben: |
| |
|
|
 |
D ist dabei der Diffusionskoeffizient
der Elektronen oder Löcher. |
 |
Den Diffusionskoeffizienten der Elektronen
oder Löcher haben wir schon mal kurz kennengelernt, er wurde als "formal
immer definierbar" bezeichnet. Aber das ist nun doch ein wenig unbefriedigend. Einge Fragen drängen sich auf: |
|
 |
Wieso diffundieren die Elektronen oder Löcher jetzt?
Bisher haben wir ihre Bewegung im Kristall ganz anders, nämlich auf zwei Weisen betrachtet: |
|
 |
- Elektronen wurden durch ebene, stehende, oder sonstige Wellen
beschrieben. Dabei haben wir nur Aufenthaltswahrscheinlichkeiten betrachtet; eine Bewegung war allenfalls indirekt über
den mit dem Wellenvektor
k verknüpften Impuls vorhanden. "Random walk" kam gar
nicht vor.
- Elektronen wurden als Teilchen betrachtet, die wegen des
Pauli Prinzips mit mit relativ hoher Geschwindigkeit durch den Kristall rasen müssen. "Random
walk" kam indirekt vor: Bei jedem "random" Stoß, wechseln sie "random" Richtung
und Geschwindigkeit. Die entscheidende Größe war aber die Driftgeschwindigkeit
vD, die wiederum mit der treibenden Kraft "elektrisches Feld"
E über die Materialkonstante Beweglichkeit m verknüpft war
|
| |
|
|
 |
Die Beweglichkeit war eine Materialkonstante, die pauschal
die im jeweiligen Material vorliegende Situation bezüglich der Stöße von Elektronen mit z.B. Defekten und
Phononen wiedergab. Mehr zu diesem durchaus nicht trivialem Thema im Link. |
 |
Die Diffusionkonstante, wie wir sie bei der
Beschreibung der Diffusion durch die Fickschen Gesetze
kennengelernt haben, macht aber im Grunde dasselbe für irgendein Teilchen, das sich in einem Medium bewegt und als
treibende Kraft einen Konzentrationsgradienten sieht. |
|
 |
Es bedurfte des Genies von Albert Einstein,
um zu erkennen, daß ein Diffusionskoeffizient oder eine Beweglichkeit
im Grunde dasselbe Elementarphänomen beschreiben: |
|
 |
Sie sind einfach Zahlen, in denen alle Einflüsse
statistisch zusammengefaßt sind, die ein Teilchen spürt, das unter der Wirkung
irgendeiner treibenden Kraft in einem Material herumgeschubst wird. |
|
 |
Einstein (und Nernst,
und Smoluchowski) leitete dann mit einigem, aber überschaubarem
Aufwand folgende einfache Beziehung ab (bekannt als Einstein-Beziehung, Einstein-Smoluchowski-Beziehung,
oder auch Einstein-Nernst-Beziehung) |
| |
|
|
 |
Abgesehen von dem Faktor kT/e sind Diffusionskoeffizient und Beweglichkeit also
identisch. Wer sich die Herleitung
anschauen möchte, kann das über den Link tun. |
 |
Da wir µ
kennen, kennen wir jetzt auch D. Damit können wir bei Kenntnis
von L oder
t die jeweils andere Größe berechnen. |
|
 |
Was noch bleibt, ist eine etwas quantitativere Vorstellung davon zu bekommen, wie groß
L oder t in einem gegebenen Material sein wird. |
 |
Unsere Grunderkenntnis von Kapitel 4 gilt natürlich immer noch: In
direkten Halbleitern ist t
klein (Größenordnung ns); in indirekten Halbleitern
ist sie groß (Größenordnung ms). |
|
 |
Wie groß oder klein genau? Das ist eine der "guten"
Fragen, die nicht so leicht zu beantworten ist. Wer sich traut, schaut via Link in eine Vorlesung
für Fortgeschrittene, der Rest (und die Mutigen) merkt sich nur einen einzigen
Zusammenhang: |
|
 |
Die Lebensdauer in indirekten Halbleitern, inbesondere
also in Silizium, ist extrem sensitiv auf Kristallgitterdefekte, insbesondere atomare Fehlstellen. Wir schauen uns das an einem Beispiel an |
| |
|
 |
Die Lebensdauer verringert sich linear mit der Goldkonzentration. Selbst bei der
kleinen Konzentration von 1014 cm –3 (» 2
ppb)
beträgt sie nur 1 µs. Bis zu einer Lebendauer von 1 ms (das
war die Behauptung) fehlen noch drei Größenordnungen – die Goldkonzentration müßte also
bei 2 ppt
liegen, um die Millisekunde zu erreichen. |
|
 |
So ist es auch! "Life time killer" wie Gold
(und viele andere metallische Fremdatome, am schlimmsten Fe, Ni, Cu) sind allesamt "tiefe Störstellen" mit Energieniveaus für
Elektronen, die tief in der Bandlücke liegen. Der Halbleitertechnologe fürchtet sie wie der Teufel das Weihwasser.
|
|
 |
An dieser Stelle liegt eine der Wurzeln der extremen Reinheits- und Perfektionsanforderungen
der Si-Technologie. Kristalle
verschmutzen gern (bei höherer Temperatur). Der Kampf für Reinheit ist deshalb immer ein Kampf gegen die Entropie – und das kostet Energie (und vor allem viel Geld).
|
|
 |
Hier steckt auch das Grundproblem der Si-Solarik:
Gute Solarzellen kann man nur aus Si mit möglichst großer Diffusionslänge und damit Lebensdauer machen.
Und diese Sorte Si kann einfach nicht billig sein! |
| |
|
© H. Föll (MaWi 2 Skript)