5.3 Vom idealen zum realen Halbleiter

5.3.1 Beweglichkeit und Leitfähigkeit bei dotierten Halbleitern

Beweglichkeit

	Um von der Ladungsträgerdichte n zur Leitfähigkeit s = q · n · µ zu kommen, brauchen wir noch die Beweglichkeit µ der Ladungsträger.
		Die Beweglichkeit µ wurde schon mehrfach angesprochen; wir hatten:
		Die Definition von µ. Den Zusammenhang zwischen µ und fundamentalen Größen wie Driftgeschwindigkeit, mittlere freie Weglänge oder Zeit zwischen zwei Stößen. Die Berechnung von µ für mehrere gleichzeitig vorliegende Stoßprozesse. Die experimentelle Bestimmung von µ mit Hilfe des Hall Effekts. Den Zusammenhang zwischen maximaler Frequenz eines Bauelementes und µ.
		Ebenfalls angesprochen wurde, daß die Beweglichkeit ein fundamentaler Materialparameter ist, und nicht nur in Formeln für die Leitfähigkeit vorkommt.
		Außerdem haben wir bereits bedauert, daß wir hier nicht in der Lage sind, Formeln für Beweglichkeiten zu finden.
	Dies alles, plus einige weiterführende Betrachtungen sind in einem eigenen Modul noch einmal zusammengestellt.
		Wie auch immer, hier müssen wir nur zwei Dinge betrachten:
		Die Beweglichkeit nimmt mit zunehmender Temperatur ab. Das haben wir bereits für den intrinsischen Fall betrachtet, und daran wird sich auch bei dotierten Halbleitern nicht viel ändern können. Die Beweglichkeit wird durch Stöße mit Fremdatomen verringert. Dotieratome sind Fremdatome, wir müssen uns also fragen ob Dotierung die Beweglichkeit beeinflußt.
		Die Antwort auf die Frage in Punkt 2 ist: Ja!. Die Beweglichkeit wird durch Dotieren herabgesetzt (das ist schlecht, da wir damit offenbar auch die Grenzfrequenz eines Bauelementes herabsetzen).
		Aber gleichzeitig wird die Temperaturabhängigkeit der Beweglichkeit verringert, da Stöße mit Phononen mit zunehmender Dotierkonzentration eine immer kleinere Rolle spielen.
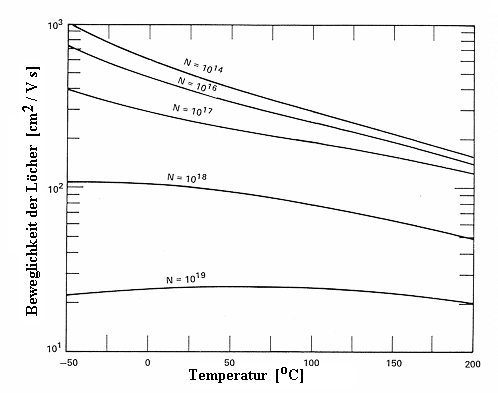
	Was wir insgesamt erhalten, sieht typischerweise so aus:
		Die Beweglichkeit wird durch Dotieren bei Raumtemperatur im Extremfall um etwa eine Größenordnung reduziert; dabei ist die Abnahme von µ erst bei höheren Dotierstoffkonzentrationen (> 1017 cm –3) richtig spürbar.
		Die Kurven für Elektronen sind ähnlich, aber im Absolutwert kann schon mal ein Faktor 10 auftauchen - je nach Halbleiter und detaillierter Bandstruktur. Die Beweglichkeit der Elektronen im Silizium ist beispielsweise ungefähr einen Faktor 3 größer als die der Löcher.

	Leitfähigkeit
	Nehmen wir die ungefähr lineare Abhängigkeit der Ladungsträgerdichte, und die vergleichweise kleine, aber nichtlineare Abhängigkeit der Beweglichkeit von der Dotierstoffkonzentration und multiplizieren beides miteinander, erhalten wir die spezifische Leitfähigkeit s oder den spezifischen Widerstand r = 1/s als Funktion der Dotierstoffkonzentration.
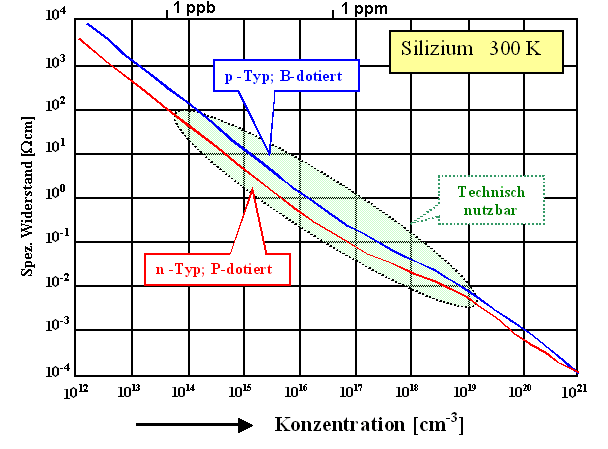
		Für Silizium sieht das dann so aus:
	Das sind so mit die wichtigsten Kurven der modernen Menschheit. Auf ihnen beruht die komplette Silizium Technologie.
		Jede Produktherstellung in der Si Technologie beginnt mit einer sorgfältigen Überlegung, mit welchem Dotiertyp und welcher Grunddotierung man startet (i.d.R. so im Bereich (10 - 0,5) Wcm)
		Bei der Herstellung eines Chips, also einer integrierten Schaltung, wird dann lokal noch bis zu 10 mal anders dotiert - darauf beruht die Funktion der Bauemente.
		Die Funktion des Systems, nur um das hier gleich mal zu unterscheiden, beruht dann darauf, wie man die Bauelemente miteinander verbindet. Das findet dann im wesentlichen nicht mehr im Si statt, sondern auf dem Si.
		Fragebogen / Questionaire Multiple Choice Fragen zu 5.3.1

© H. Föll (MaWi 2 Skript)