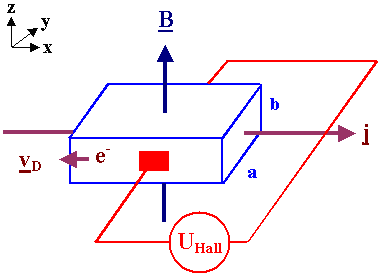
|
It is relatively easy to calculate the magnitude of the Hall
voltage UHall that is induced by the magnetic field B. |
|
 |
First we note that we must also have an electrical field E parallel to
j because it is the driving force for the current. |
|
 |
Second, we know that a magnetic field at right angles to a current causes a force
on the moving carriers, the so-called Lorentz
force
FL, that is given by
|
| |
|
|
 |
We have to take the drift velocity vD of the carriers,
because the other velocities (and the forces caused by these componentes) cancel to zero on average. The vector product
assures that FL is perpendicular to vD and B. |
|
 |
Note that instead the usual word "electron" the neutral term carrier is used, because in principle an electrical current could also be carried by charged
particles other than electrons, e.g. positively charged ions. Remember a simple but important
picture given before! |
 |
For the geometry above, the Lorentz force FL
has only a component in y - direction and we can use a scalar equation for it. Fy
is given by |
| |
|
|
 |
We have to be a bit careful: We know that the force is in y-direction,
but we do no longer know the sign. It changes if either q, vD, or Bz
changes direction and we have to be aware of that. |
|
 |
However, it is important to note that for a fixed current density jx
the direction of the Lorentz force is independent of the sign of the charge carriers – the sign of the charge and
the sign of the drift velocity just cancel each other. |
 |
With vD = µ · E and µ
=
mobility of
the carriers, we obtain a rather simple equation for the force |
|
|
|
 |
This means that the current of carriers will be deflected from a straight line
in y-direction. In other words, there is a component of the velocity in y-direction and the
surfaces perpendicular to the y-direction will become charged as soon as the current (or the magnetic field)
is switched on. The flow-lines of the carriers will look like this: |
| |
|
|
 |
The charging of the surfaces is unavoidable, because some of the carriers eventually will
end up at the surface where they are "stuck". |
|
 |
Notice that the sign of the charge for a given surface depends on the sign of the charge of
the carriers. Negatively charged electrons (e- in the picture) end up on the surface opposite to posively
charged carriers (called h+ in the picture). |
|
 |
Notice, too, that the direction of the force Fy is the same
for both types of carriers, simply because both q and vD change signs in the force
formula |
 |
The surface charge then induces an electrical field Ey
in y-direction which opposes the Lorentz force; it tries to move the carriers back. |
|
 |
In
equilibrium, the Lorentz force Fy and the force from
the electrical field Ey in y-direction (which is of course simply q ·
Ey) must be equal with opposite signs. We therefore obtain |
| |
| – q · Ey |
= |
– |q| · µ · Ex · Bz
| | | |
| | Ey |
= |
sgn(q) · µ · Ex · Bz |
|
|
 |
The Hall voltage UHall now is simply the
field in y-direction multiplied by the dimension dy in y-direction. |
|
 |
It is clear then that the (easily measured) Hall voltage is a direct
measure of the mobility µ of the carriers involved, and that its sign
or polarity will change if the sign of the charges flowing changes. |
 |
It is customary to define a Hall coefficient
RHall for a given material. |
|
 |
This can be done in different, but equivalent ways. In the link
we look at a definition that is particularly suited for measurements. Here we use the following definition: |
| |
|
 |
In other words, we expect that the Hall voltage Ey
· dy (with dy = dimension in y-direction) is proportional
to the current(density) j and the magnetic field strength B, which are, after all, the main
experimental parameters (besides the trivial dimensions of the specimen): |
| |
|
 |
The Hall coefficient is a material parameter, indeed, because we
will get different numbers for RHall if we do experiments with identical magnetic fields and current
densities, but different materials. The Hall coefficient, as mentioned before, has interesting properties: |
|
 |
RHall will change its sign, if the sign of the carriers
is changed because then Ey changes its sign, too. It thus indicates in the most unambiguous way
imaginable if positive or negative charges carry the current. |
|
 |
RHall allows to obtain the mobility µ of
the carriers, too, as we will see immediately. |
 |
RHall is easily calculated:
Using the equation for Ey from above, and the basic equation
jx = s · Ex, we obtain for negatively
charged carriers: |
| |
| RHall |
= – |
µ · Ex · Bz
s · Ex · Bz |
= – | µ
s | = |
– µ
|q| · n · µ |
= |
– 1
|q| · n |
|
|
 |
The blue part corresponds to the derivation given in the link;
n is (obviously) the carrier concentration. |
|
 |
If one knows the Hall coefficient or the carrier concentration,
the Hall effect can be used to measure magnetic field strengths B ( not so easily done otherwise!). |
 |
Measurements of the Hall coefficient of materials with a known
conductivity (something easily measurable) thus give us directly the mobility of the
carriers responsible for the conductance. |
|
 |
The minus sign above is obtained for electrons,
i.e. negative charges. |
|
 |
If positively charged carriers would be involved, the Hall constant would be positive.
|
|
 |
Note that while it is not always easy to measure the numerical value of the Hall voltage and
thus of R with good precision, it is the easiest thing in the world to measure the polarity
of a voltage. |
 |
Let's look at a few experimental data: |
| |
| Material |
Li | Cu |
Ag | Au |
Al | Be |
In |
Semiconductors
(e.g. Si, Ge, GaAs, InP,...) |
R
(× 10–24)
cgs units |
–1,89 | –0,6 |
–1,0 | –0,8 |
+1,136 |
+2,7 |
+1,774 |
positive or negative values,
depending on "doping" | Comments:
1. the positive values for the metals were measured under somewhat special conditions
(low temperatures; single crystals with special orientations), for other conditions negative values can be obtained, too.
2. The units are not important in the case, but multiplying with 9 · 1013 yields the
value in m3/Coulomb |
|
© H. Föll (MaWi 2 Skript)