4.3.2 Direkte und indirekte Halbleiter

Zwei Möglichkeiten des Banddiagramms

Zeichen wir ein E(k)-Diagramm in einem reduzierten Bandschema, gibt es genau zwei Möglichkeiten für dieBandkanten:

1. Das Maximum des Valenzbandes (definiert die Lage der Valenzbandkante) sitzt im k-Raum genau unter dem Minimum des Leitungsbandes (Die Maxima und Minima definieren dann die Lage der Leitungsbandkante).

2. Das Maximum des Valenzbandes und das Minimum des Leitungsbandes liegen bei verschiedenen k -Werten.

Wir schauen uns mal an, wie das (schematisch) in realen Materialien aussieht:

In der oberen Reihe sind Minima und Maxima übereinander; wir nennen Materialien mit dieser Eigenschaft direkte Halbleiter. Das freie Elektronengas als Referenz gehört formal auch dazu.

Die untere Reihe zeigt die indirekten Halbleiter (wir zählen den Diamant mal dazu, obwohl er eigentlich ein Isolator ist). Man beachte, daß auch Germanium ein indirekter Halbleiter ist, denn Maximum und Minimum liegen eben nicht beim selbem k-Wert und lassen sich auch nicht durch Addition oder Subtraktion von reziproken Gittervektoren untereinander bringen.

Möglichkeiten der Rekombination

Wie kommt ein Elektron im Leitungsband wieder zurück ins Valenzband? Muß es überhaupt wieder zurück?

Wir machen ein Gedankenexperiment und bestrahlen einen Halbleiter dauerhaft mit Licht. Jedes Photon wirft ein Elektron ins Leitungsband, und es gibt keine Rekombination.

Dann sind irgendwann alle Elektronen im Valenzband "ausgeräumt" und befinden sich im Leitungsband, wo sie auch bleiben. Das Material hat jetzt eine gute Leitfähigkeit und würde sie auch auch nach Abschalten des Lichts behalten. Falls das Material bei Tageslicht eine Zeit lang herumlag, wäre es für immer ein Leiter.

Das klingt sehr, sehr unwahrscheinlich. Während wir beleuchten haben wir zwar eine gewisse Leitfähigkeit s_L (wir könnten jetzt also schon einen Photowiderstand bauen), aber sobald das Licht ausgeschaltet wird, geht sie erfahrungsgemäß sehr schnell wieder auf den Dunkelwert s_D zurück.

Ab Ausschaltzeitpunkt finden wir dann das übliche exponentielle Abklingen mit

s(t)	= s_D + s_L · exp –	æ ç è	t t	ö ÷ ø

Wie schnell ist schnell? In anderen Worten wie groß ist die Zeitkonstante t des Prozesses und was bestimmt sie?

Da das Abklingen der Leitfähigkeit das Verschwinden der Elektronen im Leitungsband via Rekombination widerspiegelt, ist t schlicht und ergreifend die mittlere Lebensdauer der Elektronen im Leitungsband.

In anderen Worten: Nachdem ein Elektron ins Leitungsband befördert wurde, (wobei es natürlich nicht darauf ankommt, wie genau das geschah) wird es sich dort (im Mittel) eine gewisse Zeit lang herumtreiben (im Ortsraum, es ist ja beweglich), und dann per Rekombination wieder verschwinden. Und diese Zeit des Verbleibens im Leitungsband heißt passenderweise "Lebensdauer".

Für die Löcher im Valenzband gilt natürlich exakt dasselbe. Ihre Lebensdauer ist identisch zu der der Elektronen.

Soweit ist eine Beobachtung beschrieben - und sie gilt für direkte und indirekte Halbleiter. Rekombination wird erfolgen, und wir können auch schon eine erste Zahl damit verbinden.

Wie genau erfolgt nun Rekombination und was passiert dabei? Wir haben immer noch Energie und Kristallimpulserhaltungssatz zu beachten.

Für direkte Halbleiter ist die Antwort einfach: Elektron und Loch können sich jederzeit nach der Thermalisierung wieder vereinigen; der Kristallimpulserhaltungssatz ist gewahrt. Die freiwerdende Energie ist auch kein Problem: Sie wird zu Licht, d.h. zu einer elektromagnetischen Welle.

Es gibt auch keinen Grund, warum das nicht recht zügig passieren soll - die Lebensdauer der Elektronen ist entsprechend klein und liegt im Nanosekundenbereich.

Wir können für direkte Halbleiter den Kreis jetzt also schließen:

Wenige Nanosekunden nachdem ein Photon mit irgendeiner Energie ³ E_G ein Elektron - Loch Paar generiert hat, ist es auch schon wieder verschwunden - unter Aussendung eines Photons mit der präzisen Energie hn = E_G. Die Differenz der Photonenenergien vorher - nachher geht als Wärme ins Gitter.

Wir reden auch dann von Rekombination - und es ist wichtig, sich darüber klar zu sein - wenn irgendein Elektron aus dem Leitungsband mit irgendeinem Loch imValenzband rekombiniert.

Wie die Elektronen und Löcher ursprünglich entstanden sind ist unerheblich. Spätestens nach der Thermalisierung gibt es keine "Erinnerung" mehr an den Entstehungsprozeß. Was für photogenerierte Elektronen (und Löcher) gilt, gilt für jedes Elektron (und Loch)!

Wir merken uns: In direkten Halbleitern kann man durch Rekombination von Elektronen und Löchern Licht erzeugen. Direkte Halbleiter sind die Materialien der Optoelektronik!

Wie sieht der gesamte Prozeß in einer Bandiagrammdarstellung aus?

Das kommt darauf an, was für eine Variable man an die Abszisse schreibt. Schaun' mer mal:

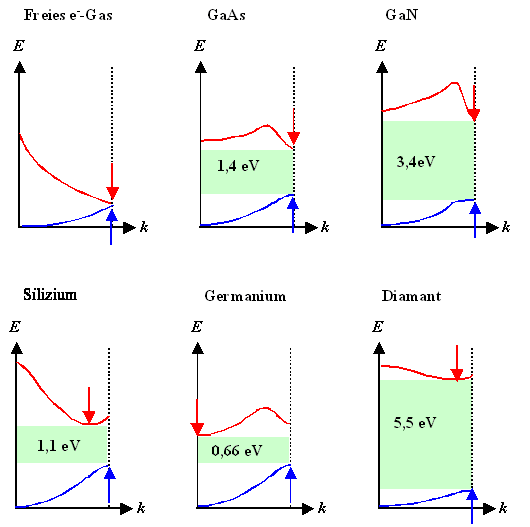
Links eine Auftragung über den Wellenvektor. Dann sieht das Ganze ähnlich aus wie im Bild oben mit den Dispersionskurven.

Rechts nehmen wir als Abszisse mal den Ort (oder die Zeit). Und realisieren, dass Elektron und Loch nur im k-Raum "ortsfest" sind. Im realen Raum werden sie herumvagabundieren, in einem uns bereits bekannten "random walk". Bis zur Rekombination vergeht im Mittel die Zeit t; die zurückgelegte Strecke ist eine Diffusionslänge L. Das ist so richtig nicht darstellbar, wir behelfen uns mit den "gezackten" Kurven. Wir werden diese Thematik weiter unten noch einmal aufgreifen.

Schon das Vorhandenseins eines Wellenvektors bedeutet ja, daß die "Elektronenwelle" sich i. a. bewegt. Was wir hier aber stillschweigend gemacht haben, ist der Übergang vom Wellenbild (des freien Elektronengases) zum Teilchenbild der Banddiagramme. Das kann man schlicht ignorieren; beide "Bilder" sind gleichberechtigt, welches man nimmt ist Geschmackssache oder eben durch Zweckmäßigkeit diktiert. Mehr dazu in einem extra Modul.

Beide Übergänge müssen wieder senkrecht nach oben oder unten stattfinden, denn beide beteiligte Teilchen müssen zur selben Zeit am selben Ort sein, damit sie was miteinander haben können. Im rechten Bild ist sofort klar, daß der Rekombinationspartner eher nicht der Generationspartner war. Denn es ist ziemlich unwahrscheinlich, dass die beiden sich jemals wieder begegnen.

Im Bild ist deshalb auch ein anderes Loch - woher auch immer stammend - gezeigt. Unser Elektron interessiert sich aber auch gar nicht dafür, mit welchem Loch es sich vereinigt, denn alle Elektronen und damit auch alle Löcher sind gleich, sie sind prinzipiell ununterscheidbar. Nur der Zustand, in dem sie sich befinden, kann unterschiedlich sein!

Zunächst aber: Was aber passiert in indirekten Halbleitern? Offenbar muß es auch in diesen Materialien Mechanismen der Rekombination geben.

Einfach: Wenn zwei Teilchen miteinander agieren sollen, das aber aus (Kristall)impulserhaltungsgründen nicht können, braucht man eben einen dritten Partner.

Der Kristall kann es nicht sein; bleiben nur noch Kristallgitterdefekte. Genau so ist es auch: In Si, Ge, und so weiter, erfolgt Rekombination über Defekte, vorzugsweise Fremdatome. Der Defekt kann Impuls und Energie aufnehmen; es wird dann aber kein Licht emittiert.

Wir können sofort eine Vorhersage machen:

Bei indirekten Halbleitern ist die Lebensdauer von Elektronen im Leitungsband tendenziell hoch und wird unmittelbar und stark von der Defektkonzentration abhängen.

Genauso ist es. Im handelsüblichen sehr perfekten und ultrareinem Silizium ist die Lebensdauer t von Unendlich kaum zu unterscheiden (aus Sicht des Elektrons): Sie liegt bei einigen Millisekunden. In dieser extrem langen Zeit (aus Sicht eines Elektrons), läuft das Elektron in einem "random walk" durchs Gitter.

Dabei kommt es sehr weit. Bis zu seinem Ableben nach (im Mittel) t Sekunden legt es (im Mittel) eine Strecke L zurück, die Diffusionslänge heißt

L	=	æ è	D_e,h · t	ö ø	1/2

zurück; D_e,h ist der formal immer definierbare Diffusionskoeffizient der Elektronen oder Löcher; ein neuer Materialparameter wenn man so will. Wir können aber schon jetzt erwarten, daß der hiermit eingeführte Diffusionkoeffizient der Elektronen und Löcher irgenwie mit der schon früher definierten Beweglichkeit m und ihrer mittleren Geschwindigkeit v₀ zusammenhängt - all diese Größen beschreiben ja "irgendwie" die Bewegung der Teilchen. Einen Zusammenhang zwischen m und v₀ hatten wir im übrigen schon mal gefunden.

Die gemessenen Werte für L liegen für ultrareines Si in der Größenordnung Millimeter - wahrlich eine lange Strecke für ein kleines Elektron! In direkten Halbleitern, in denen die Elektronen und Löcher selbstverständlich auch herumdiffundieren, liegt die Diffusionslänge im nm Bereich.

In völlig verdrecktem, d.h. nach chemischer Nomenklatur aber evtl. immer noch höchstreinem Si, sind Lebensdauer und Diffusionlänge reduziert auf µs und µm; und dies wird unmittelbare Auswirkungen auf Halbleiterbauelemente wie z.B Solarzellen haben.

Wir merken uns: Indirekte Halbleiter sind nicht als Leuchtquellen geeignet. Die Rekombination wird sehr stark von Kristallgitterdefekten beeinflußt.

Kann ich einem Stück Halbleiter "ansehen" ob es eine direkte oder indirekte Bandlücke hat? Nun ja - mit Einschränkungen schon.

Ich muß nur schauen, wie die Lichtabsorption als Funktion der Frequenz läuft. Setzt sie bei einer bestimmtem Frequenz schlagartig und kräftig ein, habe ich einen direkten Halbleiter. Denn sobald hn = E_G wird Absorption möglich.

In einem indirekten Halbleiter kann bei hn = E_G nicht kräftig absorbiert werden, denn es gibt bei dieser Energie ja keinen direkten Übergang. Erst bei höheren Photonenenergien, die hn_direkt, dem direkten Übergang mit der kleinsten Energie entsprechen, wird Absorption kräftig einsetzen. Im Frequenzbereich zwischen hn = E_G und hn_direkt wird zwar auch absorbiert (über komplexere Mechanismen), aber eher verhalten.

Messungen des Absorptionskoeffizientens a sehen so aus; a definiert sich über das übliche "Abklinggesetz":

Intensität(x)	= Intensität(x = 0) · exp –a · x

Si und Ge sind die einzigen indirekten Halbleiter in diesem Diagramm, man sieht den weichen Einsatz der Absorption sehr deutlich.

Fragebogen / Questionaire
Multiple Choice Fragen zu 4.3.2