|
Band-Band Übergänge werden möglich, falls ein Elektron im Valenzband
mindestens die Energie EG "zur Verfügung" hat. Dies folgt aus dem Energieerhaltungssatz. |
|
 |
Die notwendige Energiezufuhr kann sowohl von Phononen
(= thermische Energie kT) als auch von Photonen (= Licht) stammen. |
|
 |
Das dann im Leitungsband "sitzende" Elektron kann sich über die
vielen freien Plätze sehr schnell "nach unten" in das Leitungsbandenergieminimum begeben; die Überschußenergie geht als Wärme ans Gitter. Dieser Prozeß
heißt "Thermalisierung" oder dielektrische Relaxation;
er benötigt typischerweise 10–12 s. |
 |
Im Valenzband ist jetzt ein freier Platz; ein "Loch".
Diese Loch wandert ebenfalls sehr schnell "nach oben" zum Valenzbandenergiemaximum - indem Elektronen "nach unten" in das Loch fallen. |
 |
Bei Band-Band-Übergängen ist aber wie immer
außer der Energieerhaltung auch die Impulserhaltung zu beachten. |
|
 |
Die Differenz aus Impuls vorher - Impuls nachher ist proportional zu k
– k'; sie muß vom Kristall "übernommen" werden. |
|
 |
Der (quantenmechanische) Kristallimpulserhaltungssatz
ist einfach die Braggbedingung aber jetzt auch für unelastische
Streuung:: |
| |
k – k' = G
|k| ¹ |k'|
G = reziproker Gittervektor |
|
|
 |
Damit sind Band-Band-Übergänge in der Dispersionkurvendarstellung "geometrisch"
festgelegt; nur Übergänge zwischen exakt definierten Zuständen sind möglich. |
 |
Das läßt sich graphisch sehr leicht darstellen indem man die Dispersionskurven
in ein reduziertes Banddiagramm einträgt. |
|
 |
Jeder Zweig der Dispersionkurve wird um den zur BZ gehörenden reziproken
Gittervektor Richtung Ursprung verschoben; dann landet jeder Zweig in der 1.BZ |
|
 |
Man spart damit nicht nur Platz, sondern hat eine einfache Darstellung der Kristallimpulserhaltung:
Nur "senkrechte" Übergänge sind erlaubt. |
 |
Je nach genauer Struktur der Dispersionkurven gibt es für die reduzierte
Bandstrukturdarstellung zwei grundsätzlich verschiedene Grundstrukturen: |
|
 |
1. Valenzbandenergiemaximum und Leitungsbandenergieminimum liegen senkrecht übereinander. Das sind dann die direkten Halbleiter.
|
|
 |
2. Valenzbandenergiemaximum und Leitungsbandenergieminimum liegen nicht senkrecht übereinander. Das sind
dann die indirekten Halbleiter. |
 |
Elektronen werden nicht für ewig im Leitungsband bleiben - sie rekombinieren
nach einer typischen Zeit die Lebensdauer heißt mit einem Loch im Valenzband.
Auch für diese Rekombination gilt der Energie- und (Kristall)impulserhaltungsatz. |
|
 |
Für direkte Halbleiter ist Rekombination problemlos möglich. Impulserhaltung
ist gegeben, da der Rekombinationsübergang senkrecht nach unten führt, Energieerhaltung wird durch Aussendung
eines Photons gewährleistet. |
|
 |
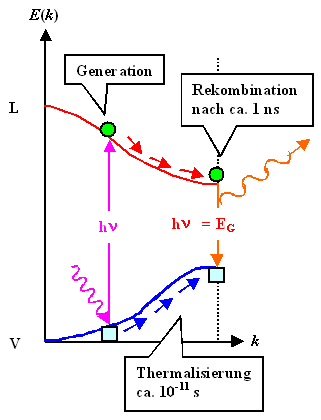
Der gesamte Kreisprozeß aus Generation, Thermalisierung und Rekombination
ist im Bild unten in allen Details dargestellt. |
|
|
|
 |
Nach der Thermalisierung steht das Elektron (und das Loch ) nicht still, sondern
"diffundiert" mit einem "random walk" durch den Kristall. |
|
 |
Wir sind jetzt im "Teilchenbild", aber auch im "Wellenbild"
läuft das Elektron hin und her; der "Zufall " des Random walks kommt durch ständige Streuprozesse an
den im realen Kristall vorhandenen Defekten. Das Teilchenbild ist jetzt vorteilhafter als das im freien Elektronengas bemühte
Wellenbild. |
 |
Nochmal: Während ihrer Lebensdauer t stehen
die Teilchen nicht still, sondern laufen in einem "random walk" durch den Kristall. Es gelten die alten Beziehungen
zwischen Zeit der Wanderung (= Lebensdauer
t), Diffusionskoeffizient
De,h (ein neuer Materialparameter) und Diffusionslänge
L (= zurückgelegte Strecke zwischen Geburt und Tod) |
|
|
|
 |
Bei indirekten Halbleitern ist t und L klein
(ns und nm), bei indirekten Halbeitern tendenziell groß (ms und mm). Allerdings sind beide
Größe extrem sensitiv auf geringste Spuren von Defekten/Verunreinigungen; "dreckiges" Si (mit
Verunreingigungsgehalten im ppb - ppm Bereich) hat sehr viel kleinere Lebensdauern und Diffusionslängen. |
 |
Ob ein Halbleiter direkt oder indirekt ist, zeigt sich auch in seinem Absorptionsverhalten
als Funktion der Wellenlänge. |
© H. Föll (MaWi 2 Skript)