|
Wir betrachten jetzt nur noch Halbleiter.
Sie unterscheiden sich von Isolatoren zunächst nur durch die Möglichkeit,
daß die bei Raumtemperatur verfügbare thermische Energie kTRT
» 1/40 eV ausreicht, um einigen Elektronen den Sprung vom (vollen) Valenzband ins Leitungsband
zu ermöglichen. |
|
 |
Der Übergang von Elektronen vom Valenzband ins Leitungsband sowie der umgekehrte
Prozeß, der Übergang von Elektronen im Leitungsband zu freien Plätzen im Valenzband, sogenannte Band-Band-Übergänge, sind also unmittelbar verantwortlich für die elektrische
Leitfähigkeit der Halbleiter. Wir müssen sie etwas näher betrachten. |
|
 |
Jeder solcher Übergang bedeutet einen Wechsel von einem Zustand mit einem Wellenvektor
k zu einem neuen Zustand mit einem Wellenvektor k'. Dabei ändert sich die
Energie und der Impuls des Elektrons. |
|
 |
Da aber der Energie- und Impulserhaltungssatz auch in der Quantentheorie gilt, müssen
wir uns mit den damit verbunden Konsequenzen beschäftigen. |
 |
Wir betrachten zunächst den Energieerhaltungssatz.
Um von der etwas undeutlichen "thermischen Energie" wegzukommen, nehmen wir Photonen,
also Licht, mit der eindeutig definierten Energie EPhoton=h · n,
um Elektronen aus dem Valenz- ins Leitungsband zu lupfen. |
|
 |
Wir betrachten nun das Schicksal eines von einem Photon getroffenen Elektrons
im Detail, sowohl im E(k)-Diagramm als auch im Banddiagramm. |
| |
|
 |
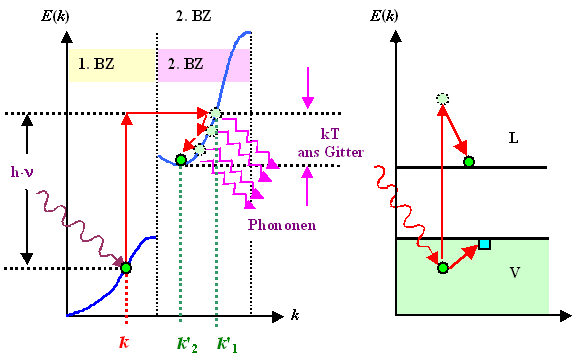
Das Photon trifft ein Elektron irgend"wo" im Valenzband. Das "wo"
bezieht sich dabei sowohl auf den Ort im Ortsraum als auch im k-Raum. In der Zeichnung hat das "getroffene"
Elektron den Zustand k; damit ist alles über den Zustand "vorher" gesagt. Es gibt nun
zwei Möglichkeiten: |
 |
1. Die Energie des Photons hn reicht
aus, um das Elektron mindestens bis zur Leitungsbandunterkante zu heben. Dann wird das mit einer gewissen Wahrscheinlichkeit
auch passieren. Im Bild reicht die Energie sogar um ein Elektron deutlich über die Leitungsbandkante zu heben (roter
Pfeil nach oben). |
|
 |
Im E(k)-Diagramm gibt es aber hn über
dem Zustand k gar keinen Zustand; wir müssen das Elektron also in
den energetisch passenden Zustand in der 2.
BZ "transferieren" (roter Pfeil nach rechts). Dadurch hat das Elektron jetzt aber einen anderen (größeren)
Wellenvektor. |
|
 |
Wir folgen den beiden roten Pfeilen; das Elektron sitzt nun im Zustand k'1
im sonst leeren Leitungsband. |
|
 |
Es gibt jetzt jede Menge freie Plätze bei kleineren Energien für unser Elektron
- es wird also nicht lange auf seinem ersten Platz bleiben, sondern sich von Platz zu Platz "nach unten" sinken
lassen, bis es das Energieminimum des Leitungsbandes bei k'2
erreicht hat; angedeutet durch die kleinen roten Pfeile nach unten. |
|
 |
Die Überschußenergie geht dabei portionsweise ins Gitter - der Kristall wird ein
bißchen wärmer. In der Zeichnung ist das formal-abstrakt so dargestellt, daß das Elektron beim Hinunterhüpfen
ins Leitungsband Phononen emittiert. |
|
 |
Dieser Prozeß heißt Thermalisierung oder dielektrische Relaxation. Er
erfolgt sehr schnell - in (10– 11 - 10– 13) s
ist alles vorbei. |
 |
2. Die Energie des Photons ist zu klein; sie reicht nicht
aus, um einen Übergang Valenzband - Leitungsband zu induzieren. |
|
 |
Dies bedeutet, daß es für hn <
EG
keine Absorption des Photons geben kann. Für Photonen mit kleinerer Energie ist
der (perfekte) Kristall komplett durchsichtig. |
|
 |
Wir haben also auch fundamentale optische Eigenschaften im Banddiagramm enthalten! |
 |
Die Darstellung im Banddiagramm rechts ist natürlich viel einfacher, weil
wir uns nicht um die k-Werte kümmern. Wir können dafür eine andere wichtige Sache besser
wiedergeben als im E(k)-Diagramm: |
|
 |
Das ins Leitungsband transferierte Elektron hinterläßt einen unbesetzten
Platz im Valenzband, ein "Loch"; als kleines blaues Quadrat
eingezeichnet. |
|
 |
Das gibt dem energetisch direkt über dem Loch sitzenden
Elektron die Möglichkeit, energetisch etwas tiefer zu sinken, indem es den freien Platz besetzt. Die freiwerdende Energie
geht wieder als Wärme ins Gitter. |
|
 |
Das Loch ist jetzt energetisch eins höher gerutscht.
Das direkt darübersitzende Elektron.... - der Prozeß wiederholt sich, bis das Loch an der Valenzbandoberkante sitzt. |
|
 |
Im Banddiagramm haben wir jetzt ein Elektron an der Leitungsbandkante
(wir meinen dann immer die untere Kante) und ein Loch an der Valenzbandkante
(wir meinen dann immer die obere Kante). |
|
 |
Die Position von Loch und Elektron ist dann irgend"wo" - denn die Ordinate des Banddiagramms
trägt keine Bezeichnung; wir lassen alles unspezifiziert. Das ist auch richtig, denn obwohl Elektron und Loch gleich
nach der Generation einen definierten Ort besitzen, sind sie ja beweglich und laufen - per "random walk" - irgendwo
hin. |
 |
Damit haben wir energetisch alles im Griff.
Der Energiesatz ist in jedem Moment erfüllt, die Energie des gesamten System aus Photon, Elektron und Kristall (mit
Phononen) ist konstant. |
|
 |
Wie steht es mit dem Impulserhaltungssatz?
|
| |
|
|
Impulserhaltung beim Band
- Band Übergang |
| |
|
 |
Wir müssen nun den Impuls des Systems
vorher und nachher betrachten. Das ist erheblich
schwieriger als die Betrachtung der Energie, da der quantenmechanische Impuls von Photon, Kristall und Elektron nicht so
unmittelbar klar ist wie die Energie. |
|
 |
Wir müssen hier etwas an der Oberfläche bleiben, und werden einige "Dinge"
einfach postulieren. Trotzdem läßt sich eine wichtige Beziehung leicht verständlich
machen. |
|
 |
In der Quantenmechanik ist der Impuls immer gegeben durch |
| |
| Impuls |
= p = 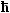 · k · k |
|
|
|
 |
- und das gilt für Elektronen, Photonen und Phononen. Da die Wellenlängen von (Licht)Photonen
immer sehr viel gößer sind als die der Elektronen und Phononen
(Photonen liegen im 1 µm Bereich, Elektronen und (die hier wichtigen) Phonen eher im nm Bereich); der
Wellenvektor dann entsprechend viel kleiner, können wir den Impuls der Photonen in 1.
Näherung schlicht vernachlässigen. |
|
 |
Im Link ist das ein bißchen genauer
aufgeführt. Es ist hilfreich, sich in diesem Zusammenhang schlicht folgende Regel zu merken: |
| |
Photonen haben Energie, aber kaum Impuls.
Phononen haben Impuls, aber kaum Energie.
Elektronen haben Impuls und Energie. |
|
|
 |
Damit können wir den Impuls der Photonen erst mal "vergessen";
und Phononen sind bei der primären Generation auch noch nicht beteiligt. Es geht damit nur noch um den Impuls des Elektrons
vorher (im Valenzband; Wellenvektor k) und nachher (im Leitungsband; Wellenvektor k');
dafür schreiben wir Dp, die Differenz des Impulses vorher – nachher.
|
|
 |
Wir haben |
|
|
| Dp = |
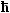 · (k – k') · (k – k') |
|
|
|
 |
Diese Differenz ist auf jeden Fall ungleich Null, d.h. der Impulserhaltungssatz ist für
das Elektron ohne dritten Partner nicht zu erfüllen. |
 |
Der dritte Partner in einem perfekten Kristall kann aber nur der Kristall selbst
sein. Er hat die Masse ¥ verglichen mit einem Elektron, und könnte eigentlich
damit jeden beliebigen Impuls aufnehmen - so wie die Hauswand beim Ballspiel. |
|
 |
Kann er aber nicht. In der Quantenmechanik sind die Dinge
gequantelt, und die Differenz (k – k') kann nur diskrete
Werte annehmen. |
|
 |
Welche das sind können wir hier nicht herleiten. Wir können aber das Ergebnis, auch
als Kristallimpulserhaltungssatz bekannt, zur Kenntnis nehmen; es lautet |
| |
k – k' = G
G = reziproker Gittervektor |
|
 |
Das sollte uns nun sehr bekannt vorkommen. Es ist die gute alte Bragg-Bedingung mit einer Verallgemeinerung:
|
|
 |
|k|=|k'| muß nicht mehr
erfüllt sein!, wir lassen jetzt auch inelastische Streuung zu. |
|
 |
Das ist nun wirklich einfach, hat aber einschneidende Konsequenzen. |
 |
Wenn wir die Darstellung des Band-Band-Übergangs im E(k)-Diagramm
oben wieder betrachten, bedeutet Impulserhaltung nun, daß der nach rechts weisende
rote Pfeil die Länge eines reziproken Gittervektors haben muß. |
|
 |
Das hat er aber sicher nicht, denn in der Zeichnung wäre der kürzestmögliche
reziproke Gittervektor so lang wie beide Brillouinzonen zusammen (man betrachte ein früheres
Bild, falls das nicht unmittelbar einsichtig ist). |
|
 |
Die Konsequenz is einfach: der oben gezeichnete Band-Band-Übergang kann gar nicht stattfinden, er verletzt den Kristallimpulserhaltungssatz! |
 |
Um Energie- und Kristallimpulserhaltung gleichzeitig
zu erfüllen. müssen wir nun im E(k)- Diagramm solange mit zwei
vorgegeben Strecken (den beiden roten Pfeilen) an der Dispersionskurve rauf- und runterfahren, bis wir einen k-Wert
finden, bei dem alles paßt. |
|
 |
Das tun wir aber nicht, sondern wir lassen uns etwas einfallen, was die Arbeit sehr stark
erleichtert: Wir benutzen ab sofort ein reduziertes Bandschema oder Banddiagramm. |
|
| |
| |
Reduziertes Banddiagramm
|
| | |
 |
Die
E(k)-Diagramme wie schon mehrfach gezeigt, lassen sich sehr viel platzsparender zeichnen, wenn man
eine kleine Vereinbarung bezüglich eines zeichentechnischen "Tricks" trifft: |
|
 |
Wir malen alle Zweige der E(k) Kurven in den diversen Brillouin
Zonen in die 1. Brillouin Zone. Man weiß ja, zu welcher BZ irgendein Ast gehört - man muß
nur von unten kommen abzählen. |
|
 |
Praktisch geht das ganz einfach: Wir verschieben jeden Ast solange um reziproke Gittervektoren
nach innen, bis er in die 1. BZ fällt. Das sieht so aus: |
| |
|
 |
Diese "Spar"version der Dispersionkurven heißt reduzierte Darstellung oder reduziertes Banddiagramm. |
|
 |
Nebenbei erwähnt: Die reduzierte Darstellung des Banddiagramms ist nicht nur ein Zeichentrick,
sondern geht etwas tiefer. Man kann zeigen, dass die Addition eines reziproken Gittervektors zum Wellenvektor einer beliebigen
Kristallwellenfunktion (fast) nichts ändert. Das ist hier aber nicht so wichtig, wer will kann sich das Ganze im Link noch etwas genauer anschauen. |
 |
Damit sparen wir nicht nur eine Menge Platz, sondern die von Impuls- und Energieerhaltungssatz
aus erlaubten Übergänge liegen jetzt einfach senkrecht übereinander. |
| |
| |
|
 |
Das ist leicht einzusehen: Jeder Übergang der energetisch paßt, erfüllt
automatisch den Kristallimpulserhaltungssatz, denn die diversen Äste der E(k) Kurve unterscheiden
sich ja genau durch einen reziproken Gittervektor. |
|
|
 |
Die Absorption eines Photons sieht jetzt also so aus wie links dargestellt. Die Länge
des Pfeils mit der Energie hn muß nur noch an die passende Stelle zwischen den zwei
Ästen gezeichnet werden. |
 |
Wir wollen diese Vereinbarung, für Band-Band-Übergänge das reduzierte
Bandschema zu verwenden, zukünftig automatisch einhalten. Sie ist im übrigen auch durch die harte Theorie zu rechtfertigen,
die unter der Bezeichnung "Bloch
Theorem" bekannt ist. |
 |
Band-Band-Übergänge zeichnen wir zukünftig auch im einfachen Banddiagramm nur
noch senkrecht nach oben - und nach unten. |
| |
 |
Die typischen Kurve eines reduzierten Banddiagramms wie nebenstehend gezeigt, taucht in der
Natur häufiger auf. Wir beobachten sie bei genauem Hinsehen auch bei Objekten,
die der Halbleiterphysik eher fern stehen. Ein aufmerksamer Betrachter kann auch noch Hinweise auf Komplikationen finden,
die wir erst in den folgende Kapiteln behandeln werden. |
|
|
|
 |
Denn alles was wir bisher gelernt haben gilt selbstverständlich
nicht nur für die Generation von Elektronen, d.h. für
die Schaffung eines Elektron-Loch Paares durch den Übergang eines Elektrons vom Valenz- ins Leitungsband, sondern auch
für die Rekombination, die Wiedervereinigung von Elektron und Loch.
|
|
 |
Versuchen wir, das im obigen Bild einzutragen, bekommen
wir ein Problem. |
|
 |
Nach der Thermalisierung
von Elektron und Loch, sitzen sie im gezeichneten Beispiel nicht mehr senkrecht übereinander!
Ein Übergang nach unten und damit Rekombination ist ohne Verletzung des Kristallimpulserhaltungssatzes nicht möglich! |
 |
Das ist eine ziemlich aufregende Erkenntnis - mit weitreichenden Konsequenzen.
Wir werden ihr ein eigenes Unterkapitel widmen. |
|
|
|
© H. Föll (MaWi 2 Skript)