 |
Wir haben mehrfach direkt oder indirekt gelernt, dass für alle (freien) Teilchen
oder Quasiteilchen, die dann immer durch eine ebene Welle mit Wellenvektor k = 2w/l und einer Kreisfrequenz w beschreibbar sind, in der Quantentheorie
für Gesamtenergie E und Impuls p sehr einfache Gleichungen gelten: |
| |
| E | = |
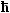 · w · w |
| p | = |
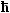 · k · k |
|
|
|
 |
Heißt das, dass alle Teilchem mit demselben Wellenvektor auch dieselbe
Energie haben? Nein - heißt es nicht, denn die Beziehung zwischen w
und k ist die Dispersionsrelation, und die kann für verschiedene
Teilchen sehr verschieden sein. |
 |
Schauen wir uns das mal konkret an - für unsere Teilchen Elektron
und Photon, sowie für das Quasiteilchen Phonon. |
|
 |
Was wissen wir über die Wellenvektoren, Frequenzen und Dispersionsrelationen für
dieses Dreigestirn? Eine ganze Menge, aber wir haben das nie so ganz systematisch dargestellt. Schaun' mer mal; aber nur
ganz grob - wir betrachten ausschließlich Größenordnungen. |
 |
Photonen. Wir interessieren uns hier
nur für Infrarot (IR) - Ultraviolett (UV), also das Spektrum rund ums sichtbare Licht. Wir haben folgende
Eigenschaften: |
|
 |
Wellenlängen von Licht, wie oben definiert,
weiß man einfach. Sie liegen so um 5 µm - 0.1 µm. Damit haben
wir Wellenvektoren im Bereich (106 - 5 · 107) m–1.
|
|
 |
Frequenzen weiß man nicht einfach, man kann
aber nachschauen, oder sie mit der nachfolgenden Gleichung berechnen. Wir haben jedenfalls w
» (4 · 1014 – 2 · 1016) s–1. |
|
 |
Die Dispersionsrelation des Lichtes kennen wir vielleicht nicht unter diesem Namen, aber was wir kennen müssen
ist die elementare Beziehung |
| |
| c = n · l = |
w
2p | · |
2p
k | = |
w
k |
|
|
|
 |
Dabei ist c natürlich die Lichtgeschindigkeit, also im Vakuum ca. 3 ·
108 m/s - das weiß man. Und - hey- wir haben hier ja schon eine Dispersionsrelation,
eine Beziehung zwischen w und k für elektromagnetische Wellen (im Vakuum). |
 |
Die freien Elektronen des
Kristalls tummeln sich alle in den ersten Brillouinzonen. Damit wissen
wir: |
|
 |
Die Wellenvektoren liegen maximal
so um (einige) p/a; Mit einer Gitterkonstanten a so um 0.3 nm
(weiß man), haben die energiereichen Elektronen Wellenvektoren so um k
= 1010 m–1, und damit Wellenlängen im nm Bereich. |
|
 |
Selbstverständlich kann man im Rahmen des freien Elektronengasmodells auch kleine k's
bis k = 0 haben, aber diese Elektronen sind verhältnismäßig uninteressant. |
|
 |
Die Dispersionsrelation
- diesmal für die Energie - kennen wir, sie lautet |
|
|
Ek = 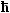 · wk = · wk = |
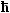 2 · k2 2 · k2
2me |
|
|
|
 |
Daraus können wir die Frequenzen berechnen und erhalten
|
| |
| wk = |
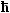 · k2 · k2
2me |
» |
10–34 · 1020 J · s
2 · 9.1 · 10–31
kg · m2 |
» 5 · 1015 |
kg · m2 · s
s2 · kg · m2 |
» 5 · 1015 Hz |
|
|
|
 |
Wie der Zufall (???) so spielt, ist das dieselbe Größenordnung
wie bei den Photonen. |
 |
Bleiben noch die Phononen. Hier wissen
wir gar nichts, es sei denn wir haben den entsprechenden Fortgeschrittenen
Modul gelesen. Falls nicht, tun wir das jetzt. Dann können wir folgende Angaben machen: |
|
 |
Wellenvektor: Ist ähnlich wie bei den
Elektronen maximal p/a, d.h. er liegt in der ersten Brillouinzone. |
|
 |
Frequenz: Maximal ca. 1013 Hz;
die Kreisfrequenz kann dann 1014 Hz sein. |
|
 |
Die Dispersionsrelation für den den einfachst möglichen Fall (nur ein Atom in der
Basis) lautet (und das muss man hier einfach glauben): |
|
|
| w | = |
æ
ç
è |
2Y · a
ma |
æ
è | 1 – cos(ka) |
ö
ø | ö
÷
ø
| 1/2 |
|
|
|
 |
Dabei ist Y der Elastizitätsmodul und ma die Masse
des Atoms. |
| |
|
 |
Mit den obigen Zahlen können wir jetzt die Größenordnungen für
Energie und Impuls unserer drei Teilchen berechen. |
|
 |
Dazu legen wir eine Tabelle an |
| |
| | Photon |
Elektron | Phonon |
| Wellenvektor k |
107 m–1 |
1010 m–1 |
1010 m–1 |
| Frequenz w |
4 · 1015 Hz | 4 · 1015 Hz |
1014 Hz |
Energie E = 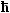 · w · w |
2.4 eV | 2.4 eV | 0.06 eV |
Impuls p = 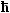 · k · k |
107 · 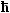 · m–1 · m–1 |
1010 · 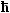 · m–1 · m–1 |
1010 · 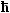 · m–1 · m–1 |
 » 6 · 10–16 eV/s
» 6 · 10–16 eV/s |
|
 |
Was lernen wir daraus? Etwas sehr wichtiges: Salopp ausgedrückt gilt: |
|
 |
Photonen haben Energie, aber kaum Impuls. |
|
 |
Phononen haben Impuls, aber kaum Energie. |
|
 |
Elektronen haben Impuls und
Energie. |
 |
Daraus folgt sofort: |
|
 |
Bei einer Wechselwirkung von nur zwei der drei Teilchen, kann der Impuls- und Energieerhaltungssatz
i.a. nicht erfüllt werden. |
|
 |
Deshalb sind z.B. bei der Interaktion von Licht (= Photonen) mit einem Kristall (= freie Elektronen)
fast immer auch Phononen beteiligt. |
|
| |
© H. Föll (MaWi 2 Skript)
![]() 4.3.1 Grundsaetzliche Ueberlegungen und reduziertes Bandschema
4.3.1 Grundsaetzliche Ueberlegungen und reduziertes Bandschema