|
Die Beweglichkeit der Ladungsträger ist ein Maß für die Stöße
mit Defekten aller Art (inkl. "Phononen", den Quasipartikeln der quantisierten thermischen Vibrationen). |
|
 |
Dotieratome sind Defekte, die Beweglichkeit
wird also mit steigender Dotierstoffkonzentration abnehmen (das ist schlecht). |
|
 |
Gleichzeitig wird aber die Temperaturabhängigkeit schwächer (das ist
gut). |
 |
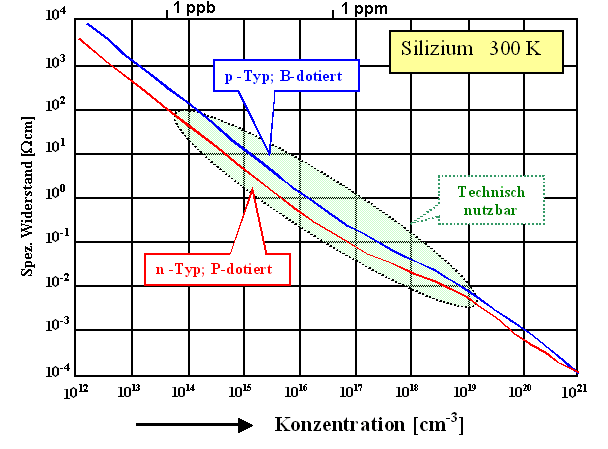
Die Leitfähigkeit
s = q · n · µ ist damit fast nur noch von der (Majoritäts)ladungsträgerdichte
abhängig; es ergeben sich für Si die folgenden (für die Menschheit sehr wichtigen) Kurven für
den spez. Widerstand r = 1/s. |
| |
|
 |
Bei der Betrachtung von Generations und Rekombinationsprozessen zwischen Valenz-
und Leitungsband sind jetzt die Minoritätsladungsträger viel interessanter als die Majoritäten, da bei letzeren
die Konzentrationsänderungen durch diese Prozesse viel kleiner sind. |
|
 |
Im Gleichgewicht gilt nach wie vor |
| |
|
 |
Während ihrer Lebensdauer t entfernen sich
die Minoritäten im Mittel um die Diffusionslänge L von ihrem "Geburtsplatz", es gilt wie
bei jedem "random walk" |
|
|
|
|
 |
Die in dieser Gleichung formal auftauchende Diffusionskonstante D
spiegelt wie die Beweglichkeit µ die Stoßprozesse wieder, denn ohne viele (statistische) Stöße
gibt es keinen "random walk". |
|
 |
Beweglichkeit und Diffusionkonstante müssen deshalb korreliert sein, es
gilt die Einstein-Smoluchowski Beziehung |
| |
|
 |
Lebensdauern, und damit Diffusionslängen, sind in indirekten Halbleitern
sehr stark von Defekten bestimmt und in vielen Größenordnungen variierbar. |
|
 |
Konzentrationen von atomaren Fehlstellen im ppt (= 10–12)
Bereich können bereits die Lebensdauer von Halbleiter (i.d.R. Si) "versauen", d.h. so stark reduzieren,
dass die Bauelementfunktion leidet. |
© H. Föll (MaWi 2 Skript)