|
Die bisher behandelten intrinsischen Halbleiter sind zwar faszinierende Materialien
zur Entwicklung der vollen Theorie der elektronischen Eigenschaften von Festkörpern, aber nicht so furchtbar spannend
für Anwendungen. Das hat zwei Gründe |
|
 |
1. Die Leitfähigkeit ist extrem temperaturabhängig. Das ist
sehr nachteilig für Anwendungen - außer man will ein Thermometer bauen. |
|
 |
2. Man muß die intrinsischen Halbleiter nehmen wie man sie bekommt - die Eigenschaften
sind was sie sind. Das ist natürlich auch ganz schlecht - wir wollen schließlich Eigenschaften in möglichst
weiten Grenzen so einstellen, wie wir sie haben möchten (das nennt man Technologie). |
 |
Der zweite Punkt ist sogar zweifach schlecht.
Erstens, weil wir die Eigenschaften des idealen intrinsischen Kristalls (über den
wir hier immer noch reden) so nehmen müssen wie sie sind, und zweitens, weil wir
gar keinen idealen Kristall bekommen, sondern immer einen mit mehr oder weniger viel Defekten. Und was für elektronische Eigenschaftsänderungen mit den Defekten mitgeliefert werden, wissen wir noch
nicht. |
|
 |
Wir kommen also nicht umhin, uns den elektronischen Eigenschaften eines Kristalls mit Defekten zu widmen, den Eigenschaften des Realkristalls.
Dabei können uns maximal drei Fälle unterlaufen: |
|
 |
1. irgendwelche Defekte
(Leerstellen, Fremdatome, Korngrenzen, ...) beeinflussen Ladungsgträgerdichte und Beweglichkeiten
gar nicht oder kaum. Nicht sehr wahrscheinlich, aber auch nicht verboten. |
|
 |
2. Defekte nehmen Einfluß - in einer Art und Weise, die uns nicht
gefällt. Das hört sich nicht nur realistisch an, das ist sehr real!
|
|
 |
2. Defekte nehmen Einfluß - in einer Art und Weise, die uns gefällt.
Das gibt es glücklicherweise auch - hier liegt die Quelle der gesamten Festkörperelektronik. |
 |
Der Einbau einer genau passenden Menge
einer geeigneten Defektart in den richtigen Teilbereich
eines Halbleiterkristalls heißt "den Kristall dotieren"; alles andere heißt
"den Kristall versauen". |
|
 |
Man kann es gar nicht drastisch genug ausdrücken: Dotieren,
das A und O der Halbleitertechnik, ist eine schwierige Sache, auch wenn es dafür inzwischen viele ausgereifte
Techniken gibt. Versauen, dagegen, ist immer einfach. |
 |
Dotiert wird (fast) immer bei allen Halbleitern, indem substitutionelle Fremdatome eingebaut werden, die Dotieratome. Wir betrachten
aber im folgenden nur noch Silizium, um die Übersichtlichkeit zu gewährleisten. Das Prinzip
ist aber für alle Halbleiter gleich. |
|
 |
Das Prinzip besteht darin, ein Si Atom durch ein Gruppe
III oder Gruppe V Atom
zu ersetzen. In anderen Worten: Es wird ein Atom eingebaut, das ein Elektron weniger oder mehr hat als ein Si
Atom. Und damit auch ein Elektron zu wenig oder eins zu viel um die sp3 Hybridorbitale absättigen zu können. |
|
 |
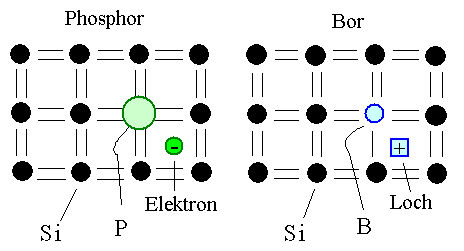
Das schauen wir uns in einem schematischen Kristallbindungsbild mal an |
| |
|
|
 |
Selbstverständlich ist Si kein Kristall mit einer Atomanordnung in der Fläche
wie gezeigt (sondern ???), aber so lassen sich die
zwei Elektronen in den vier Bindungen am besten zeichnen (als Strich). |
 |
Wo immer nun ein Gruppe V Atom sitzt - und in der Si Praxis werden
das immer entweder ein P- oder ein As-Atom sein; eher selten mal noch Sb - gibt es ein Elektron zuviel. Dieses überzählige Elektron ist noch (locker) an das Dotieratom gebunden |
|
 |
Falls wir diesem Elektron einen Stoß geben, z.B. durch thermische Energie, wird es sich
losreißen können - und dann gehört es nicht mehr zum Dotieratom, sondern zum Kristall und ist frei beweglich. |
|
 |
In anderen Worten: Wird genügend Energie zugeführt, um das Überschußelektron
aus seiner noch bestehenden Bindung herauslösen zu können, "sitzt" es jetzt im Leitungsband
- wo sonst? |
|
 |
Denn nur im Leitungsband gibt es überhaupt freie Plätze für Elektronen - und
ein Elektron ist ein Elektron ist ein Elektron - der Kristall weiß nicht, wem es mal "gehörte". Sitzen tut es im übrigen nur energetisch - auf einem Platz in Zustandsraum - ansonsten kann
sich "frei" bewegen. |
|
 |
Zurück bleibt ein einfach positiv
geladenes P+- oder As+- Ion. Es ist ortsfest (wir
vernachlässigen Diffusion). Ladungsneutralität
ist jetzt nur noch für den Gesamtkristall gewahrt; nicht mehr lokal. |
 |
Wo immer nun ein Gruppe III Atom sitzt - und in der Si Praxis wird
das immer nur ein B-Atom sein - gibt es ein Elektron zu wenig. Dieses freie Bindung
ist am Dotieratom lokalisiert. |
|
 |
Falls wir aber einem der Elektronen in einer benachbarten Bindung einen Stoß geben,
z.B. durch thermische Energie, wird es auf den freien Platz in der Nachbarbindung springen können. Der freie Platz
ist jetzt in der Nachbarbindung und nicht mehr am B-Atom. |
|
 |
In den normalen Bindungen aber, können Elektronen einfach so zwischen den 4
sp3 Keulen hin- und herwechseln, denn die 8 zur Verfügung stehenden Elektronen sind ja nicht
einer der Keulen fest zugeordnet. Dier freie Platz, der jetzt in einer Si-Si Bindung liegt, und den wir jetzt mal
ganz vorsichtig ein Loch nennen, ist also frei beweglich. |
|
 |
In anderen Worten: Wird einem Elektron im Valenzband genügend
Energie zugeführt, um die freie Bindung beim B-Atom abzusättigen, haben wir jetzt ein Loch
im Valenzband, das dort (per Elektron-hüpf-kette) frei beweglich ist. |
|
 |
Denn die Elektronen in den Bindungen sind natürlich nichts anderes als unsere Valenzelektronen. Man kann das sehen, indem man entweder die Entwicklung
des Valenzbandes aus den bindenden Zuständen der sp3 Hybridorbitale anschaut (das Leitungsband
ensteht aus den antibindenden Zuständen),
oder schlicht konstantiert: "Wo sonst sollen diese Elektronen sitzen?" |
|
 |
Zurück bleibt ein negativ geladenes ortsfestes B–-Ion. Ladungsneutralität ist wiederum nur noch für den Gesamtkristall gewahrt; nicht mehr
lokal. |
 |
Das wollen wir jetzt im Banddiagramm darstellen. Wenn man von der kleinen lokalen
Störung der Kristallparameter einmal absieht, haben wir durch dotieren lediglich
für ein paar zusätzliche Zustände für Elektronen gesorgt; Zustände,
die es vorher nicht gab. |
|
 |
Bezeichnen wir die Konzentration an Dotieratomen mit ND für
die Gruppe V Elemente, und mit NA für die Gruppe III Elemente, haben wir jetzt
ND zusätzliche Plätze irgendwo unterhalb der Leitungsbandkante
, und NA zusätzliche Plätze oberhalb der Valenzbandkante. |
|
 |
Das "irgendwo" wird dabei durch die jeweilige noch vorhandene Bindungsenergie gegeben.
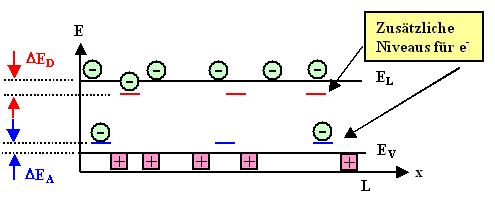
Im Banddiagramm erhalten wir folgende Darstellung |
|
|
|
 |
Wo immer auch ein Dotieratom sitzt, gibt es einen zusätzlichen Platz in der
Bandlücke, jeweils um ein dotieratomspezifisches DE unterhalb der Leitungsbandkante
oder oberhalb der Valenzbandkante. |
|
 |
DED ist dabei genau die Energie, die man
aufwenden muß, um dem Fremdatom ein Elektron wegzunehmen; DEA
ist die Energie die man gewinnt, falls ein zusätzliches Elektron am Fremdatom gebunden wird. |
|
 |
Das ist sehr ähnlich zu den guten alten Ionisationsenergien
bzw. Elektronenaffinitäten
der Atome. |
|
 |
Das bringt uns natürlich auf einen Gedanken. So wie jedes
Atom eine Ionsiationsenergie hat (nicht aber unbedingt eine positive Elektronenaffinität), müßte man eigentlich
auch jedem Fremdatom, oder wenn man weiter denkt sogar jedem Defekt,
ein Elektron entreissen können, wenn man nur genügend Energie DED
hineinsteckt. |
|
 |
Dem ist auch so - leider. Denn man kann eben nicht nur
mit Dotieratomen dotieren, sondern mit allen möglichen Defekten den Kristall versauen - siehe oben. |
| | |
|
Donatoren und Akzeptoren
|
| |
|
 |
Wir haben also grundsätzlich zwei Möglichkeiten,
um mit atomaren Fehlstellen, die wir bei Halbleitern Störstellen nennen, die Ladungsträgerkonzentration
im Leitungs und /oder Valenzband zu beeinflussen: |
|
 |
Wir können Donatoren einbauen, die in der Lage sind, eine
Elektron in das Leitungsband abzugeben. Dabei ist es zunächst unerheblich, wo genau sich das Donatorniveau
befindet, d.h. wie groß DED ist. |
|
 |
Wir können Akzeptoren einbauen, die in der Lage sind, eine
Elektron vom Valenzband zu "akzeptieren", d.h. aufzunehmen. Dabei ist es zunächst unerheblich, wo genau sich
das Akzeptorniveau befindet, d.h. wie groß DEA
ist. |
 |
Um gezielt zu dotieren, sind natürlich
Donatoren und Akzeptoren von Vorteil, deren DE Werte so klein sind, daß die
thermische Energie bei Raumtemperatur schon deutliche Effekte zeigt. |
|
 |
Das ist für die bereits genannten technisch wichtigen Dotierelemente
auch gegeben; die folgende Tabelle gibt Zahlenwerte für Si (Elemente in Klammern werden technisch nicht benutzt). |
| |
| DE [eV] |
| Donatoren | Akzeptoren |
| | P | 0.045 |
B | 0.045 |
"Flache" Störstellen
"Shallow levels"
|
| As | 0.049 | (Al) |
0.057 | | Sb | 0,039 |
(Ga) | 0,065 | | (Li) |
0,033 | (In) | 0,16 |
| | | (Mn) |
0,53 | (Cu) | 0,49 |
"Tiefe" Störstellen
"Deep levels"
|
| Zum Vergleich: kTRT
» 0.025 eV |
|
|
 |
Für technisches Dotieren sind nur die flachen Störstellen
interessant. Die tiefen Störstellen, von denen nur zwei Beispiele gezeigt sind,
können zwar dotieren (wenn auch bei Raumtemperatur nur mit Mühe), sie haben aber andere Effekte und müssen
unbedingt vermieden werden, d.h. ihre Konzentration sollten allenfalls im ppqt
(???) Bereich liegen. |
|
 |
Im übrigen muß die Störstelle nicht immer unbedingt substitutionell eingebaut
werden, interstitielle Störstellen produzieren auch Energieniveaus in der Bandlücke, tendenziell aber eher "tiefe"
Niveaus. |
 |
In einem Illustrationsmodul
findet sich eine Zusammenstellung der Energieniveaus vieler Störstellen in einigen Halbleitern |
 |
Wir haben jetzt einen Teil des eingangs beschriebenen
Programms abgehandelt: Wir wissen, daß atomare Fehlstellen zusätzliche Plätze für Elektronen in
der Bandlücke bereitstellen, wir "wissen", wo diese Plätze energetisch liegen und ob sie Elektronen
abgeben (d.h. Donatoren sind) oder aufnehmen (d.h. Akzeptoren sind).
|
|
 |
Fein. Aber was bedeutet das für die Leitfähigkeit? |
|
 |
Oder präziser gefragt: Für die Elektronendichte
nL im Leitungsband, die Löcherdichte nV im Valenzband und die jeweiligen
Beweglichkeiten µL bzw. µV ? |
|
 |
Wer halbwegs aufgepaßt hat, sollte die prinzipielle Antwort bezüglich der Konzentrationen
jetzt wissen. Also: Kurz nachdenken, dann zum nächsten Unterkapitel weiterklicken. |
| |
|
© H. Föll (MaWi 2 Skript)