|
Dichte der Elektronen im Leitungsband: |
|
| nL(T) = |
¥
ó
õ
EL |
D(E) · f(E, T) · dE |
= | 4.8 · 1015 · T
3/2 · exp – | EL – EF
kT | cm– 3 |
|
|
|
 |
Erster Teil der Formel gilt immer |
|
|
 |
Zweiter Teil der Formel enthält div. Näherungen |
|
 |
Dichte der Löcher im Valenzband |
| |
|
 |
Löcher verhalten sich wie positiv geladene Elektronen |
|
| nhV(T) = |
¥
ó
õ
EL |
D(E) · [1 – f(E, T) ] · dE |
= | 4.8 · 1015 · T
3/2 · exp – | EF – EV
kT | cm– 3 |
|
|
|
 |
Löcher haben eine positive Elementarladung, tragen Strom, haben eine Masse und eine Beweglichkeit. |
|
| |
| |
| |
 |
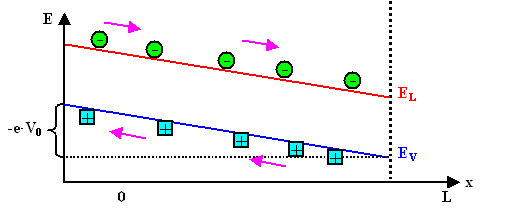
Ein elektrisches Feld "verbiegt" die Bänder um die jeweilige elektrostatische
Energie, d.h. um e · V, V = elektrostatisches Potential. |
|
|
|
 |
Die lokale Bandverbiegung zeigt die Richtung des induzierten Teilchenflusses: Elektronen "abwärts",
Löcher "aufwärts". | |
|
 |
Bei Stromfluß herrscht Nichtgleichgewicht; damit gibt es streng genommen keine Fermienergie
mehr. | |
| |
| |
|
© H. Föll (MaWi 2 Skript)