|
Phasendiagramme sind ein unerschöpfliches Thema; hier wollen wir nur noch
einige fundamentale Fälle für binäre
Phasendiagramme kennenlernen. |
|
 |
Zunächst erinnern wir uns: Jedes (binäre) Phasendiagramm ist eine Art Landkarte im Zusammensetzungs - Temperatur Raum für zwei Komponenten A und
B. Ein Phasendiagramm zeigt uns zwei Dinge: |
 |
1.
Was in einem bestimmten Gebiet vorliegt, d.h. welche Phase oder Phasen wir bei einer
gegebenen Komposition und Temperatur im Gleichgewicht finden werden. |
|
 |
Ein Gebiet sind die einheitlich gekennzeichneten Flächen
im Phasendiagramm. Grundsätzlich kann in einem Gebiet eine reine Phase vorliegen,
oder ein Gemisch von zwei Phasen. |
|
 |
Drei Phasen können nicht in einem Gebiet existieren, denn das verbietet die Phasenregel.
Bei zwei Komponenten C, und drei Phasen P,
wird die Zahl der Freiheitsgrade F
= C – P + 1 = 0. In Worten: Drei Phasen können nur an einem Punkt
im Phasendiagramm vorliegen, nicht in einem Gebiet.. |
|
 |
Beim Gleichgewicht von drei Phasen an einem
Punkt finden wir deshalb immer eine horizontale Linie; eine isotherme, auf der die drei Kompositionspunkte der drei Phasen
liegen; wir haben das bei eutektischen Umwandlungen gesehen. |
|
 |
Bei zwei Phasen existiert nur noch ein Freiheitsgrad, bei variabler Temperatur ist das die Zusammensetzung oder
Komposition der zwei Phasen |
|
2. Was sich in was umwandelt - bei
Temperatur- oder Kompositionsänderung. Das ist durch die Grenzlinien zwischen 2 Flächen gekennzeichnet. |
|
 |
Interessant sind die Umwandlungen als Folge von Temperaturänderungen; denn
das ist für ein gegebenes Material leicht zu machen. Umwandlungen durch Änderungen der Zusammensetzung sind für
ein gegebenes Material normalerweise gar nicht, oder nur sehr eingeschränkt möglich. |
 |
Es gibt zwei grundsätzliche Umwandlungsarten
falls man durch eine kleine Änderung der Temperatur eine Phasentrennlinie überquert |
 |
1. Eine Phase wandelt sich in eine zweite Phase um; wir haben eine "Reaktion"
zwischen zwei Phasen. Das ist einfach, aber auch sehr eingeschränkt, denn alle
Teilchenzahlen (der Atommix) müssen erhalten bleiben. Die Reaktionsgleichung für diesen einfachen Fall ist
|
| |
|
|
 |
Ein Beispiel ist die Umwandlung von fcc Fe in bcc Fe - für
reines Eisen. Aber schon mit minimalem Zusatz von Kohlenstoff (C) klappt das nicht mehr, da die Löslichkeit
von C in bcc Fe sehr viel kleiner ist als in fcc Fe. Die Phase "fcc Fe + 0,4% C" kann
sich nicht in die Phase bcc Fe + 0,4% C umwandeln, da es diese Phase schlicht nicht gibt. Bei der Umwandlung würde
sich bcc Fe + 0,05% C und Fe3C bilden müssen - und damit sind mehr als zwei Phasen beteiligt. |
 |
2. An der Umwandlungsreaktion sind drei
Phasen beteiligt. Die eutektische Reaktion ist ein Beispiel; die allgemeine Reaktionsgleichung lautet |
| |
|
|
 |
Für die uns schon bekannte eutektische
Reaktion war a die Flüßigphase L. In diesem Unterkapitel wollen
wir die restlichen prinzipiell möglichen Reaktionen zwischen drei Phasen kennenlernen. |
|
 |
Noch ein (eigentlich überflüssiges) Wort zur Klarheit:
Eine Phase, z.B die Flüßigphase L oder Mischkristalle, kann ohne weiteres
aus beiden Komponenten zusammengesetzt sein; und eine Mischphase kann nur eine
Komponente enthalten (z.B. eine Mischung zweier Kristallsorten). Man sollte Phasen und Komponenten nie verwechseln! |
|
 |
Im Gegensatz zu der "harten"
Definition von Phasen bezeichnen wir als "Phase" jetzt das, was in einem flächigen Gebiet des Phasendiagramms
existiert. Eine Mischphase a + b ist in diesem
Sinne nur eine Phase! Etwas verwirrend, zugegeben, aber praktisch. Im Grunde braucht
man nur die Bedingung "im Prinzip mechanisch abtrennbar" der harten Definition
etwas zu entspannen zu "mit einfachen Mitteln mechanisch abtrennbar", und
alles ist klar. Denn aus Mischphasen, in denen z.B. mikrometergroße Körner oder Lamellen aus a
im b "hocken", kann man zwar das a
prinzipiell abtrennen, aber nicht auf einfache Art
und Weise! |
 |
Das Schlüsselwort jetzt ist Umwandlung.
|
|
 |
Phasendiagramme, in denen außer einem Übergang flüssig - fest
keine weiteren Phasenumwandlungen vorkommen, die also nur aus den minimal erforderlichen zwei Phasen Liquidus und Solidus
bestehen, sind einfach und langweilig. |
|
| |
 |
|
Eine bisher nur indirekt besprochene Umwandlung, die Bildung einer stöchiometrischen
Verbindung, also eine Umwandlung der Sorte xA + yB ®
AxBy ist ebenfalls einfach und langweilig. |
|
|
|
 |
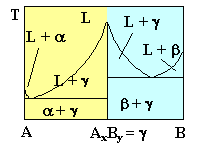
Damit wird ein Phasendiagramm nur in zwei Unterdiagramme aufgespalten, wie nebenstehend gezeigt:
A bis AxBy, und AxBy bis B. |
|
 |
Ganz so einfach ist es aber meistens dann doch nicht, wie wir noch sehen werden,
da die Verbindung AxBy möglicherweise erhebliche Mengen andere Phasen lösen kann,
und dann von einem vertikalem Strich im Phasendiagramm zu einem mehr oder weniger dicken Bereich mutiert. |
|
| | |
| |
 |
Spannender sind all die Beziehungen und Umwandlungsreaktionen, an denen drei Partner beteiligt sind; das ist wie im richtigen Leben. |
|
 |
Eine davon haben wir bereits kennengelernt: Die eutektische Reaktion, bei der zwei Phasen a
und b aus einer dritten Phase, nämlich dem Liquidus L entstehen. |
|
 |
Nochmal, die eigentlich überflüssige Wiederholung:
Die Phase a besteht aus der Komponente A plus gelöster
Komponente B; wir bezeichnen sie als Mischkristall; die Phase
b besteht aus der Komponente B plus gelöster
Komponente A. Wieviel B oder A jeweils gelöst werden kann sagt uns das Phasendiagramm. Die Phase
L besteht aus A und B in der jeweiligen Mixtur. Den denkbaren (und vorkommenden) Fall, dass A
und B als Flüßigkeiten nicht, oder nicht vollständig mischbar sind, betrachten wir hier nicht. |
|
 |
Wie all die nachfolgenden Phasendiagramme aus relativ simplen Betrachtungen des
Verhaltens der freien Enthalpie beim Mischen zweier Substanzen zustandekommen, ist in einem "Advanced"
Modul noch etwas näher ausgeführt. |
 |
Die eutektische Reaktion ist nur eine von
vier Möglichkeiten, zwischen drei Phasen eine Umwandlungsbeziehung zu haben. Wir
betrachten zunächst alle 4 Fälle in einer Tabelle |
| |
Invariante
Reaktion | Reaktionsgleichung |
Typisches Phasendiagramm
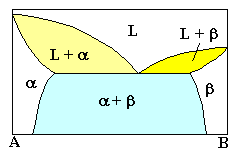
(Ausschnitt) | | Eutektisch |
L ® a + b
1 Phase ® 2 Phasen |
 |
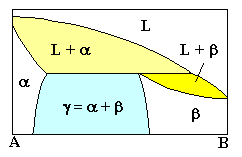
| Peritektisch |
L + b ® g
2 Phasen ® 1 Phase |
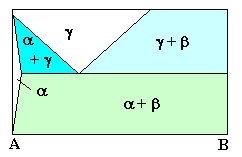
 | | Eutektoid | g
® a + b
1 Phase ® 2 Phasen |
 |
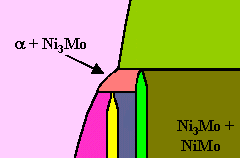
| Peritektoid |
a + g ® b
2 Phasen ® 1 Phase |
 |
|
|
 |
Das war's. Mehr Möglichkeiten gibt es nicht für Umwandlungen, die beim
Abkühlen erfolgen |
 |
In allen vier Fällen stehen bei einer bestimmten Temperatur drei
Phasen miteinander im Gleichgewicht. (Bei der peritektoiden Reaktion darf jeder mal selbst versuchen, ob er sie findet;
dabei kann man auch das komplette Phasendiagramm zu Hilfe nehmen). |
|
|
|
 |
Das sind nicht, wie man
immer wieder versucht ist zu denken, die "Phasen", die in den Flächen um den "Punkt" herum stehen;
z.B L + a, L + b, a + b
in der eutektischen Reaktion ganz oben. Denn das alles sind keine reinen Phasen, sondern
Mischphasen; bestehend aus zwei reinen Phasen. |
|
|
|
 |
Was in der eutektischen Reaktion bei der eutektischen Temperatur im Gleichgewicht steht sind
die Phasen links und rechts vom horizontalen Strich und die "echte" Phase am "Punkt": L, a
und b. | |
|
 |
Deswegen haben alle diese invarianten
Reaktionen im Phasendiagramm einen horizontalen Strich - die beteiligten Phasen müssen bei einer
Temperatur durch eine Linie verbunden sein, d.h. in Beziehung zueinander stehen.
Das ist nebenstehend für die eutektische und peritektische Reaktion hervorgehoben. |
|
|
| |
| |
|
Peritektische Umwandlung
|
| |
|
 |
Was geschieht in den vier Fällen beim Abkühlen? Das schauen wir uns
für einige Fälle etwas ausführlicher an. |
 |
Im uns schon bekannten Fall des Eutektikums
haben wir einen Liquidus, d.h. eine Schmelze, die genau die "richtige" Zusammensetzung hat und bei (im Prinzip
minimalster) Unterschreitung der eutektischen Temperatur komplett in eine Mischphase aus
a + b erstarrt. |
|
 |
Und nochmals: Dabei sind die reinen Phasen a
oder b aber bitte nicht mit den Ausgangsstoffen A
oder B zu verwechseln; sie sind viel mehr die möglichen Mischkristalle oder
"solid solutions", die bei der betrachten Temperatur existieren (und die wir nicht mit "Mischphasen"
verwechseln wollen!). |
|
 |
Wieviel a und b dannn
vorliegt, sagt uns das Hebelgesetz. |
|
 |
In anderen Worten: Die a - Phase ist die Zutat A
(also eine bestimmte Atom- oder Molekülsorte), die eine bestimmte Menge an B gelöst hat. Das können
nur einige ppm oder etliche Prozent sein - wieviel genau sagt das Phasendiagramm, wenn man im reinen a
Gebiet nachschaut. Für die b Phase gilt entsprechend dasselbe. |
 |
Im uns neuen Fall des Peritektikums (das ist
wie immer griechisch, und heißt "das darum herum gebaute" ???) ist die Sache ein wenig komplizierter: |
|
 |
In Worten haben wir jetzt: "Flüßig" + "Fest 1" ® "Fest 2" (statt: "Flüßig" ®
"Fest 1" + "Fest 2"). |
|
 |
Die schlichte Änderung der eutektische Reaktionsgleichung
L ® a + b
in die Form
L + a ® b,
kann aber etwas irreführend sein (und eigentlich müßte es ja auch L –
a ® b heißen). |
|
 |
Um das zu sehen, muß man sich nur mal den Fall betrachten, dass die Mischkristallphasen
a und b fast reines A oder B sind, d.h.
die Löslichkeit von A in B und andersherum ist praktisch = 0. |
|
 |
Eine Reaktionsgleichung der Art L + a ® b wäre dann gleichbedeutend mit L + A ® B - und das geht nicht! |
|
 |
L enthält sowohl A als auch B; und man kann durch Zugabe von mehr
A zu L schlicht und ergreifend nicht reines B erzeugen. |
 |
Deswegen schreiben wir L + a ® g und lassen zunächst mal offen was
genau g sein soll. |
|
 |
Denn für g ist vieles möglich. Aus L
+ a kann b entstehen - falls genügend A
in b löslich ist. |
|
 |
g kann aber auch eine Verbindung des Typs AxBy
(mit noch gelöstem A und/oder B sein), und schlußendlich kann g
auch noch (etwas unpräzise) für eine Mischphase a + b
stehen. |
 |
Was geschieht beim Abkühlen eines Peritektikums? Bei der peritektischen Temperatur
haben wir die die Phasen a, g und L ins Gleichgewicht zu setzen.
|
| |
|
 |
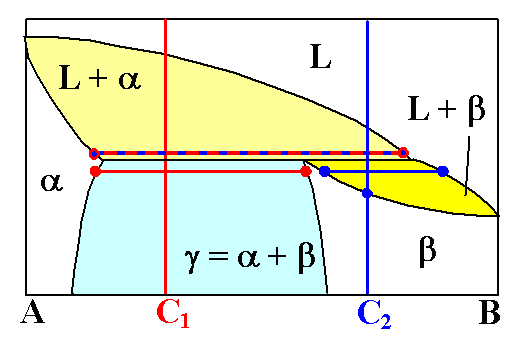
Betrachten wir zunächst die Zusammensetzung C1, d.h wir
kühlen ab entlang der roten Linie. |
|
 |
Kurz oberhalb der peritektischen Temperatur enthält die L + a
Mischphase feste a Bröckchen mit einem relative hohen A-Anteil (linker blau-roter
Punkt), die in einer L-Phase schwimmen, die einen hohen B Anteil besitzt (rechter blau-roter Punkt). Wie groß
das Verhältnis zwischen a und L
genau ist, sagt uns das Hebelgesetz. |
|
 |
Kurz unterhalb der peritektischen Temperatur finden wir jetzt eine a
+ b Mischphase; unser g aus der peritektischen Reaktionsgleichung. |
|
 |
Diese Mischphase bildet sich, indem die a Bröckchen
wachsen oder schrumpfen, bis der a - Anteil stimmt
für das was g braucht; der Rest erstarrt zu b.
Beim weiteren Abkühlen verschieben sich die relativen Anteile noch etwas, das ist aber nicht anders als zuvor. |
|
 |
Falls wir beim Erstarren zu viel a haben, wird eine Änderung
nur über Diffusionsprozesse möglich sein - und das sind l a n g s a
m e Prozesse. |
 |
Spannender ist die Zusammensetzung C2; hier geschieht die eigentliche
peritektische Umwandlung. |
|
 |
Kurz oberhalb der peritektischen Temperatur haben wir die gleiche Zusammensetzung der L
+ a Mischphase wie zuvor, nur die relativen Anteile sind anders - wir haben weniger a. |
|
 |
Kurz unterhalb der peritektischen Temperatur finden wir jetzt aber eine neue
Mischphase - bestehend aus L + b, in der eine feste Phase b
schwimmt. Die a Phase ist verschwunden! |
 |
Wie soll das geschehen? Es gibt nur eine Möglichkeit: |
|
 |
Die a-Phase kann nur verschwinden, indem sie sich in b umwandelt: Dazu muß A heraus- und B hineindiffundieren. |
|
 |
Um die sich umwandelnden a- Bröckchen wird sich gleichzeitig
reines b bilden - und durch diese Schicht muß A und B dann hindurchdiffundieren. |
|
 |
Irgendwann erstarrt dann die restliche Schmelze mehr oder weniger dicht bei der richtigen
b - Zusammensetzung. |
 |
Wie auch immer das im Einzelnen abläuft, die Rate
der Umwandlung hängt an der Diffusion im festen Zustand - und das ist ein langsamer Prozess wie wir im nächsten
Kapitel lernen werden. Nur falls wir sehr lange knapp unterhalb der peritektischen Temperatur warten, und dann sehr langsam
abkühlen, werden wir überhaupt den im Phasendiagramm ausgewiesenen Gleichgewichtszustand erreichen. |
|
 |
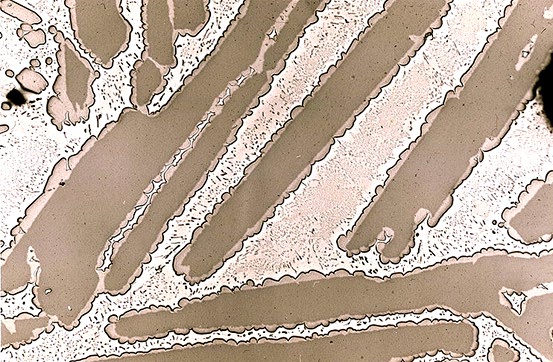
Unter normalen Umständen erwarten wir, dass noch Reste der a
- Teilchen zu finden sind, die von einer Hülle aus b überzogen sein werden.
|
|
 |
Ein solches Gefüge ist dann der "Fingerabdruck" einer peritektischen Reaktion.
Real sieht das beispielsweise im Cu - Sn System so aus . |
| |
|
|
|
|
Eutektoide und Peritektoide Umwandlung |
| | |
 |
Der Rest ist verhältnismäßig einfach |
|
 |
Ist einer der drei Partner keine Flüßigkeit, sondern eine feste Phase,
reden wir von eutektoider und peritektoider Umwandlung,
wie in der Übersicht dargestellt. |
|
 |
Der Haupunterschied ist im wesentlichen, dass alle notwendigen
Änderungen nur noch über Diffusion im festen Zustand ablaufen können
- Atome müssen durch die vorhandenen Kristalle wandern oder diffundieren, um die
notwendigen Änderungen der lokalen Konzentration zu bewerkstelligen. |
 |
Das sind grundsätzlich l a n g s a m e Prozesse, die mit abnehmender
Temperatur exponentiell noch langsamer werden. |
|
 |
Damit können wir grundsätzlich erwarten, dass die Abkühlgeschwindigkeit
eine große Rolle spielt; und daß beim "Anlassen", d.h. wieder erhitzen, noch so manches passieren kann.
|
|
 |
Denn das Phasendiagramm gibt grundsätzlich immer nur die Gleichgewichtstruktur an, und
Gleichgewicht erreicht man bei langsamen Prozessen nur, indem mam sehr lange wartet. Beim Wiedererwärmen laufen dann
die durch zu schnelles Abkühlen vorzeitig "eingefrorenen" Diffusionsprozesse
weiter, und das Gefüge ändert sich. |
 |
Eutektoide und peritektoide Reaktionen sind keine Kuriosität am Rande, sondern
in der Praxis sehr wichtig. |
|
 |
Stahl - d.h. Fe mit 0.1
% - ca. 1,5 % C "lebt" von einer eutektoiden Reaktion. Sie ist
zentral für die gesamte Stahltechnologie. Nur deshalb kann man soviele verschiedene Stahlsorten durch alle Arten von
Abkühl- und Anlaßprozesse erzeugen. |
 |
Wir sehen: Peritektische, peritektoide und eutektoide Reaktionen nur für
Gleichgewicht zu diskutieren ist nicht sehr sinnvoll. Ihre Existenz ist viel mehr der
Schlüssel zu einem Großteil der "Gefügemanipulationstechnologie", d.h. zu einem essentiellen Teil
der Materialwissenschaft und -technik |
|
 |
Wir werden uns also erst der Kinetik, der Lehre vom Weg ins Gleichgewicht zu widmen
haben, bevor wir Phasendiagramme richtig nutzen können. |
© H. Föll (MaWi 1 Skript)