5.4. Phasengleichgewichte und Phasendiagramme

5.4.1 Einfache Phasendiagramme

	Ein Phasendiagramm eines binären Systems (aus zwei Teilchensorten bestehend) ist ein Temperatur - Zusammensetzungs Diagramm, bei dem die Konzentration beider Atomsorten (cA und c B, dargestellt in Atom % oder Gewichts % ( aufpassen!)) von 0 % bis 100 % läuft.
		Für jeden Punkt mit den Koordinaten (c A,T) oder (100 – cB,T) ist die Zusammensetzung, d.h. die Phase (oder die Phasen) angegeben.
		Ein Phasendiagramm ist also eine Art Landkarte im Kompositions -Temperatur Raum.
		Dabei muß man sich aber stets vergegenwärtigen, daß Phasendiagramme ausschließlich Gleichgewichtszustände für das System AB darstellen! Wir fragen also nicht mehr "Für wieviel B in A ist A im GG mit etwas B, sondern nach der kleinstmöglichen freien Enthalpie eines System (= GG) für das die Zusammensetzung fest vorgeben ist.
	Die schlechte Nachricht ist: Es gibt keine einfachen Phasendiagramme! Selbst der einfachste Fall zweier chemisch ähnlicher Substanzen, die gut mischbar sind (d.h. HL(FA) ist klein) - z.B. im Cu und Ni oder Si und Ge System - führt zu einer Reihe von neuen Eigenschaften, die wir in diesem Kapitel kennenlernen werden.
		Es gibt aber auch keine einfachen Landkarten interessanter Landschaften. Man muß außerhalb einer brettflachen Wüste schon etwas Mühe investieren um die zugehörige Landkarte zu machen, obwohl im Prinzip klar ist was man tut.
		Die gute Nachricht ist nun: Eine Landkarte zu lesen, zu verstehen was sie beschreibt, ist viel einfacher als sie zu machen - man muß allerdings die Regeln kennen.
	Genauso ist es mit Phasendiagrammen. Um einen Satz aus dem vorhergehenden Kapitel sinngemäß zu wiederholen:
		Es ist aber klar, wie ein Phasendiagramm zustande kommt: Für jeden denkbaren Fall wird die freie Enthalpie G berechnet; die Konfiguration mit dem kleinsten G bei der betrachteten Temperatur gewinnt.
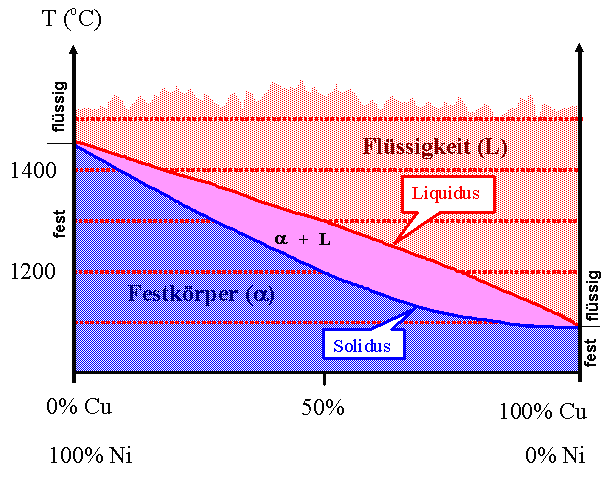
	Werfen wir zunächst einen Blick auf ein vergleichsweise sehr einfaches Phasendiagramm, das Cu - Ni Phasendiagramm, um einige Eigenschaften und Konventionen kennen zu lernen:

	Schauen wir zuerst auf die reine Ni oder Cu Seite.
		Das "Phasendiagramm" (im Grunde nur ein senkrechter Strich) zeigt zwei Phasen: das flüssige und das feste Metall (in einem fcc Gitter). Die Phasenumwandlung findet am Schmelzpunkt statt ( Ni: 1453 oC, Cu: 1083 oC).
		Hätten wir die Temperaturachse in Richtung höhere Temperaturen weitergeführt, käme als dritte Phase der jeweilige Dampf dazu.
		Das muß aber nicht immer so einfach sein. Hätten wir Fe oder Co genommen, hätten wir innerhalb der festen Phase weitere Phasenübergänge gefunden und eingetragen: Die Temperaturen, bei denen eine Umwandlung in einen anderen Gittertyp stattfindet.
	Schauen wir nun auf das komplette Phasendiagramm:
		Zunächst finden wir keine Linien, die in Anlehnung an das vorhergehende Kapitel die Löslichkeit des atomaren Defekts Cu in Ni, oder umgekehrt, angibt. Dies bedeutet, daß beide Atome unbegrenzt im jeweils anderen Kristall lösbar sind, sie formen einen Mischkristall , (um genau zu sein, einen substitutionellen Austauschmischkristall ). Das muß so sein, wenn wir ein einfaches Phasendiagramm haben möchten!
		Wir finden nur zwei Linien , die verschiedene Phasen voneinander trennen: Die "Liquiduslinie ", kurz Liquidus, oberhalb der nur eine flüssige Phase existiert, und die " Soliduslinie", kurz Solidus , unterhalb der nur eine feste Phase existiert.
		Eine der oben angesprochenen Regeln ist nun: Die flüssige Phase wird dabei immer mit einem "L", die feste(n) Phase(n) immer mit einem griechischen Buchstaben ( a, b, g,...) gekennzeichnet.
	Was für eine Phase befindet sich zwischen Liquidus und Solidus? Sie ist mit a + L gekennzeichnet, muß also eine Mischung aus zwei Phasen, aus fest und flüssig sein.
		Das ist in der Tat so: Für Wertepaare von Konzentrationen c und Temperatur T, die innerhalb der vom Solidus und Liquidus geformten "Linse" liegen, wird ein flüssig - fest Gemisch vorliegen - allerdings nicht mit der beim Mischen von Cu und Ni eingestellten Konzentration c!!! .
		Sehr merkwürdig!!!
		Wir können das dem Phasendiagramm aber nicht ganz direkt ansehen, sondern brauchen dazu eine der Regeln, die man zur Interpretation; zum "Lesen" von Phasendiagrammen benötigt.
		Die Regel ist: Gebiete, in denen eine Mischphase ausgewiesen ist, setzen sich aus den beiden Phasen zusammen, die man bei der betrachteten Temperatur auf der linken und rechten Grenze zu einem Einphasengebiet findet.
	Wir werden sofort sehen, daß alle Zustandspunkte innerhalb der a + L "Linse" instabil sind, das System wird sich in zwei Teilsysteme zerlegen wie oben beschrieben. In unserem Beispiel haben wir:
		Eine flüssige Phase mit einer Konzentration die sich aus dem Schnittpunkt der Liquiduslinie mit der gewählten Isotherme (=Linie konstanter Temperatur, auch Verbindungslinie genannt (engl. "tie line")) ergibt.
		Eine feste Phase mit einer Konzentration, die sich aus dem Schnittpunkt der Isotherme mit der Soliduslinie ergibt.
	Um das besser zu verstehen bemühen wir eine Graphik:

	Der gelbe Kreis zeigt einen Ausschnitt aus einem Phasendiagramm mit einer Liquidus- und Soliduslinie. Die Zusammensetzung unseres Substanzgemisches sei durch c0 gegeben, die Temperatur durch die gezeigte Isotherme. Wir sind mit diesen Parametern im a + L Bereich des Phasendiagramms.
		Vorliegen wird eine Mischung aus einer festen Phase mit der Zusammensetzung cS und einer flüssigen Phase mit der Zusammensetzung cL.
	Wie sieht das nun aus? Darüber sagt das Phasendiagramm direkt gar nichts - aber wir können ja mal nachdenken.
		Wir nehmen einen Behälter, einen "Tiegel", in dem wir eine Mischung aus Cu und Ni aufschmelzen. Für hohe Temperaturen ist alles flüssig; für tiefe Temperaturen ist alles fest - wie das "aussieht" ist hinreichend klar. Spannend ist nur der L + a Bereich. Was können wir erwarten?
		? Eher nicht ? Eher nicht Das wird's sein!
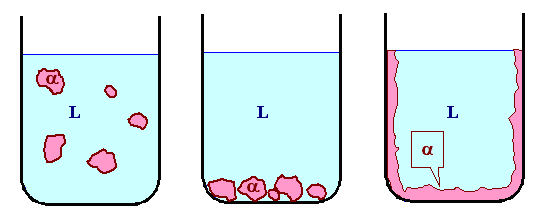
		Werden kleine a-Bröckchen in der Flüssigkeit herumschwimmen wie links gezeigt? Wohl kaum, denn das spezifische Gewicht der festen Phase ist in der Regel höher als das der flüssigen Phase (außer bei Wasser, Si und einigen wenigen anderen Exoten).
		Wir erwarten dann zumindest, daß die a-Bröckchen am Boden liegen, wie in der Mitte gezeigt (oder wie die Eiswürfel im Wasser oben schwimmen).
		Aber auch das ist nicht sehr realistisch, denn die feste Phase wird sich zuerst dort bilden, wo es beim Abkühlen am kältesten ist. Und das ist immer an der Wand des Tiegel - wo sonst? Schließlich kann die Abkühlung nur "von außen" kommen. Wir erwarten also, daß das ganze so aussieht wie rechts außen gezeigt.
		Wie groß der jeweilige Anteil der festen und flüssigen Phase ist, und wie das Ganze weitergeht wenn man nun ein bißchen weiter abkühlt, wird im nächsten Unterkapitel weiter ausgeführt. Hier wollen wir uns erstmal um den Grund für dieses Verhalten kümmern.
	Damit haben wir das Phasendiagramm und erste Auswirkungen beschrieben - mit einer Menge von unbewiesenen Behauptungen. Aber jetzt wollen wir zumindest qualitativ verstehen wie ein solches "einfaches" Phasendiagramm zustandekommt. Die herausragende Eigenschaft ist offensichtlich, daß in bestimmten Temperatur - Zusammensetzungsbereichen (innerhalb der "Linse"), zwei Phasen im Gleichgewicht koexistieren .
		Im Umkehrschluß bedeutet dies, daß eine einfache Phase , egal ob fest oder flüssig, in diesem Bereich nicht stabil ist. Die Behauptung ist dann, daß das Minimum der freien Enthalpie mit nur einer Phase nicht erreichbar ist. Falls wir das beweisen können, haben wir dieses einfache Phasendiagramm "verstanden".
		Wir schauen uns dazu die freien Enthalpien der jeweiligen Phasen als Funktion der Zusammensetzung und Temperatur an. Dies ist im nächsten Diagramm schematisch dargestellt

	Betrachen wir die drei rein schematischen Kurven. Es kommt überhaupt nicht darauf an, wie sie wirklich aussehen, die generellen Trends und die Schlußfolgerungen, die wir daraus ziehen, sind immer richtig.
		Die Enthalpie (oder, wer das lieber hat, die innere Energie U) wird von irgendeinem Wert beim Ni zu irgendeinem Wert beim Cu verlaufen. Da die Atome in dem Cu - Ni Mischkristall austauschbar sind, wird das ein relativ monotoner Verlauf sein.
		Die Entropie wird auf jeden Fall mit zunehmender Konzentration von Ni in Cu und umgekehrt kräftig zunehmen, denn wir bewegen uns von relativ perfekter Ordnung in Richtung große Unordnung. Bei ca. 50 % wird die Entropie ein Maximum haben. Im Diagramm ist – TS dargestellt; diese Funktion hat dann ein Minimum. Man nennt diesen Beitrag zur Entropie einer Phase die Mischungsentropie.
		Die freie Enthalpie ergibt sich aus der Addition beider Kurven; sie hat ein Minimum, aber nicht mehr notwendigerweise in der Gegend von 50 %.
	Diese Betrachtung gilt immer, sowohl für die flüssige Phase als auch für die feste Phase. Das Minimum in der freien Enthalpie wird aber bei kleineren Temperaturen nicht so ausgeprägt sein und vor allem kann der genaue Verlauf der freien Enthalpie in der flüssigen Phase anders sein als in der festen.
		Im nächsten Schritt vergleichen wir nun die freien Enthalpien der festen und flüssigen Phase, wobei wir Verläufe unterstellen, die obiger Kurve ähneln. Wiederum ist der genaue Verlauf aller Kurven nicht wichtig für die qualitativen Aussagen.
		Mehr ist nicht zu tun, dann wir "wissen" bereits, daß die einzigen Phasen, die vorkommen, die flüssige und die Mischkristallphase sind. Wenn wir von "first principles" starten würden, müßten wir auch andere prinzipiell mögliche Phasen betrachten.

	Wir erhalten folgendes Bild, mit aus Gründen der Klarheit stark verschiedenen G(c) - Kurven
			Bei hohen Temperaturen ist die freie Enthalpie des Festkörpers für jede Zusammensetzung höher als die der Flüßigkeit. Damit wird nur die flüssige Phase vorliegen.
			Bei etwas tieferen Temperaturen ist für einige Konzentrationen die Flüßigkeit, für alle anderen der Festkörper die Phase mit der kleinsten freien Enthalpie.
			Ein absolutes Minimum des gesamten Systems wird erhalten, wenn sich das System in zwei Phasen aufspaltet, mit Konzentrationen die aus der Tangentenregel (siehe Graphik) resultieren
			Bei weiter fallenden Temperaturen verschieben sich die Konzentrationen in den beiden Gleichgewichtsphasen wie gezeigt.
			Bei tieferen Temperaturen ist jetzt bei jeder Temperatur die feste Phase begünstigt; es wird nur eine feste Phase vorliegen.
			Im Zwei-Phasengebiet definieren die jeweiligen Gleichgewichtskonzentrationen die Liquidus- und Soliduskurve; wir erhalten das "einfache" Phasendiagramm von Cu und Ni.

	Die Tangentenregel , oben graphisch dargestellt, können wir mir Hilfe der chemischen Potentiale sofort verstehen. Da wir nur Änderungen der Teilchenzahl betrachten gilt bei festen weiteren Parametern (z.B. die Temperatur) für das Gleichgewicht
		dGSystem =  ¶G ¶nflüssig · dnflüssig  +  ¶G ¶nfest · d nfest  =  0  und d nflüssig  =  – dn fest
		Die letzte Gleichung hält nur fest, dass die Teilchen (hier immer die Summe von Ni und Cu oder, allgemeiner, A und B) entweder in der flüssigen oder festen Phase - die Gesamtzahl ist schlicht konstant.
	In unserem einfachen Fall müssen also die chemischen Potentiale gleichgroß sein, d.h.
		mflüssig  =  mfest   oder ¶ G ¶nflüssig  =  ¶ G ¶ nfest
		Beide Steigungen bei der jeweiligen Gleichgewichtskonzentration müssen gleich sein - das ist aber nichts als die Tangentenregel.

	Gibbsche Phasenregel
	Wir haben im Prinzip verstanden, daß das Ni - Cu Phasendiagramm einphasige und zweiphasige Gebiete enthalten muß, die durch Linien getrennt werden. Da wir unter der Bedingung konstanten Drucks arbeiten (wir haben Enthalpien benutzt!), können wir im Prinzip die Temperatur und die Zusammensetzung noch frei wählen (z.B. als Konzentration von Ni in Cu).
		Das funktioniert aber nur innerhalb eines einphasigen Gebiets in einem Phasendiagramm - in unserem Beispiel unterhalb der Soliduslinie. Dort ist für jede Temperatur und Konzentration eine Phase definiert, man sagt, das System hat zwei Freiheitsgrade.
		In der Mischphase dagegen, zwischen der Solidus- und Liquiduskurve, kann zwar die Temperatur noch verschiedene Werte annehmen, aber nach erfolgter Wahl einer geeigneten Temperatur sind die Konzentrationen der flüssigen und festen Phase festgelegt und damit ist alles festgelegt. Das System (beschrieben durch die Komposition c0) hat nur noch einen Freiheitsgrad.
		Verallgemeinert ist unser System gekennzeichnet durch 2 Komponenten C (hier Cu und Ni), die Zahl der Phasen P die vorliegen und die Zahl F der Freiheitsgrade, die noch möglich sind.
	Der große amerikanische Physiker Gibbs hat eine außerordentlich wichtige Beziehung zwischen diesen Größen abgeleitet, die Gibbsche Phasenregel. Sie lautet (für konstanten Druck)
		F = C  –  P  +  1

	Damit verstehen wir, warum im System Ni - Cu eine flüssige und eine feste Phase bei verschiedenen Temperaturen koexistieren kann, während in dem uns wohlvertrauten System Wasser - Eis nur bei einer bestimmten Temperatur - 0 oC - die Flüßigkeit und der Festkörper im Gleichgewicht koexistieren können. Vergleichen wir mal:
		Wasser Cu - Ni C=1 es gibt nur die Komponente H2 O C=2 wir haben Cuund Ni P =2 Flüssig und fest P=2 Flüssig und fest F=1 – 2 + 1=0 F=2 – 2 + 1=1 Es gibt keinen Freiheitsgrad mehr; alle Werte sind festgelegt; Koexistenz nur bei Tm=0oC Es gibt einen Freiheitgrad. bei fester Konzentration ist T variabel; und umgekehrt.
		Damit gilt für jedes zweiphasige Gebiet in einem Phasendiagramm, daß immer eine Aufspaltung in die zwei Phasen stattfindet , die durch die Schnittpunkte einer Isotherme mit den Trennungslinien links und rechts von dem Zweiphasengebiet definiert sind.
		Die Phasenregel und ihre Anwendung auf Phasendiagramme wird im Rückgrat 2 weiter verfolgt, wir wollen uns jetzt damit beschäftigen was passiert, wenn wir eine Schmelze mit einem Phasendiagramm wie das Cu - Ni - System bei gegebener Zusammensetzung abkühlen.
	Fragebogen ??? No. No more "muötiple choice" from here on

© H. Föll (MaWi 1 Skript)