5.4.2 Vorgänge beim Erstarren

Erstarren im Gleichgewicht

	Es ist ziemlich schwierig und zeitraubend eine Landkarte zusammenzustellen, aber es ist recht einfach, sie zu benutzen - nachdem man einige Regeln und Konventionen gelernt hat.
	Bei Phasendiagrammen ist es sehr ähnlich. Es ist sehr schwer, Phasendiagramme zu berechnen, und sehr aufwendig und zeitraubend, sie zu messen.
		Aber wenn man sie erst mal hat, können Phasendiagramme wie Landkarten benutzt werden. Aber auch dazu muß man einige Regeln und Konventionen beachten bzw. beherrschen.
		Wir werden hier aber nur die rudimentärsten Dinge behandeln! Denn: In Phasendiagrammen steckt sehr viel stark aggregierte Information. Um sie vollständig auswerten zu können, müßte man viele Wochen Zeit und Arbeit investieren. Etwas weiterführende Information findet sich im Rückgrat 2

	Schauen wir uns an, was geschieht, wenn man in einem vollständig mischbarem System, wie z.B. dem Ni - Cu System, eine gegebene Zusammensetzung von A und B aufschmilzt, und dann erstarren läßt.
		In anderen Worten: Wir gießen eine Legierung in eine Gußform. Jedesmal, wenn ein Motorblock, eine Turbinenschaufel oder eine Zahnplombe gegossen wird, laufen solche Erstarrungsvorgänge ab. Allerdings ist nicht gesagt, daß wir zu jedem Zeitpunkt im Gleichgewicht sind. Um mit Sicherheit immer Gleichgewicht zu erreichen, müßten wir nämlich extrem langsam abkühlen.
	Oder wir ziehen einen Kristall aus der Schmelze, z.B. einen Si - Ge Kristall.
		In einem Tiegel, der die flüssige Phase in der Zusammensetzung co (z.B. x % Ge und (100 - x) % Si enthält, wird ein kleiner "Impfkristall" getaucht und dann vorsichtig abgekühlt; gleichzeitig wird der Impfkristall langsam herausgezogen. Wenn man alles richtig macht, kristallisiert Si -Ge am Impfkristall und man erhält einen langsam wachsenden Kristall. Das ist das Czochralski Kristallziehverfahren; es wurde durch einen Zufall "entdeckt".
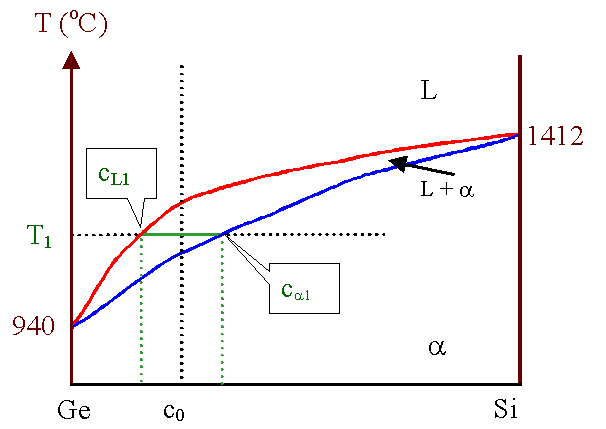
	Werfen wir zum Verständnis der Vorgänge beim  l a n g s a m e n  Abkühlen einen Blick auf das (halbwegs realistisch gezeichnete) Si - Ge - Phasendiagramm

	Betrachten wir die Zusammensetzung c0 und beginnen von einer (hohen) Temperatur T ausgehend, die Mischung abzukühlen.
		Solange T ³ TL(c0) ist, d.h. gößer als die Liquidustemperatur bei der Zusammensetzung c0, wird die Mischung komplett flüssig sein.
		Betrachten wir nun die eingezeichnete Temperatur T1. Das Phasendiagramm weist aus, daß bei T1 eine Mischung aus einer flüssigen Phase mit der Zusammensetzung cL1 und einer festen Phase mit der Zusammensetzung ca1 vorliegt.
		Die feste Phase (a - Phase) ist dabei Si - reicher als die Ausgangszusammensetzung c0, die flüssige Phase ist Ge - reicher. Es ist aber nur ein Teil des Systems kristallisiert. Wenn wir komplette Kristallisation haben wollen, müssen wir die Temperatur weiter erniedrigen.
		Tun wir das, können wir zunächst erwarten, daß der Anteil der festen Phase größer wird, der Anteil der flüssigen Phase kleiner. Gleichzeitig wird die feste und die flüssige Phase jetzt Ge - reicher.
		Dies bedeutet, daß bei einer Temperaturerniedrigung relativ zu T1 jetzt zwar etwas mehr Legierung erstarrt, aber sich die Zusammensetzung des schon vorhandenen kristallisierten Teils ändern muß: Die Ge Konzentration muß steigen. In einem Festkörper wird das nicht so einfach sein; wir brauchen dazu die Diffusion von Ge Atomen und zwangsläufig viel Zeit.
		Dieser Prozeß dauert an, bis bei T £ TSol(c0) die Mischung komplett erstarrt ist mit der globalen Zusammensetzung c0.
	Es ist aber klar, daß im realen Experiment unmöglich immer Gleichgewicht vorliegen kann. Kurz bevor wir TSol(c0) erreichen, ist das bißchen noch vorhandene Schmelze noch stark mit Ge angereichert; beim Erstarren müßte sich das überschüssige Ge im ganzen, bereits erstarrten Kristall gleichmäßig verteilen.
		Wir müssen uns also klar machen, was passiert wenn wir nicht ¥ langsam abkühlen, sondern in endlichen Zeiträumen.
		Bevor wir das aber tun, wollen wir kurz eine einfache Formel ableiten, die uns erlaubt den jeweiligen Anteil der festen und flüssigen Phase zu berechnen.

	Das Hebelgesetz
	Wie groß sind bei einer gegebenen Temperatur die jeweiligen Anteile der festen und flüssigen Phase? Auch diese Zahlen erhält man aus dem Phasendiagramm
		Kennen wir für eine gegebene Temperatur die Gleichgewichtskonzentrationen der flüssigen und festen Phase, können wir ihre relativen Anteile fL und fa leicht bestimmen
		Da die Gesamtkonzentration der festen und flüssigen Phase immer co sein muß, gilt
		co  =  fL · cL  +  fa · ca
		Da das gesamte Material in einer der beiden Anteile enthalten sein muß, gilt weiterhin .
		fL  +  fa  =  1
	Damit erhalten wir da sogenannte "Hebelgesetz"
		fa = c0 – cL ca – cL         fL = ca – c0 ca – cL

	Warum die Bezeichnung "Hebelgesetz"? Weil obige Formeln eine einfache graphische Repräsentation in Phasendiagramm haben, die an das Hebelgesetz der einfachen Mechanik erinnert.
		Um das zu sehen bilden wir den Quotienten  fa/fL, d.h. das direkte Verhältnis der beiden Konzentrationen:
		fa fL  =  c0 – cL ca – c0  =   cL – c0 c0 – ca
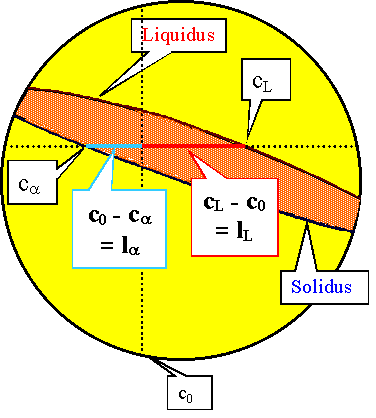
		c0 – cL (oder cL – c0, je nach "Neigung" der "Linse") ist aber genau die Strecke entlang der Isotherme von c0 bis cL, und ca – c0 (oder c0 – ca) ist die entsprechende Strecke bis ca - siehe folgende Graphik - wir können diese Strecken als "Hebel" einer Länge l interpretieren.
	Damit gilt
		Das "Gewicht" der flüssigen Phase mal dem "Hebelarm" der flüssigen Phase muß gleich Gewicht mal Hebelarm der festen Phase sein.
		fa · la  =  fL · lL
	Dazu müssen wir einige Übungen machen!
		Übung 5-4 Hebelgesetz

	Erstarren im Nichtgleichgewicht
	Was für eine Zusammensetzung hat unser Gußstück oder unser Kristall, wenn wir nicht ¥ langsam abkühlen bzw. den Kristall aus der Schmelze ziehen?
		Nachdem die flüssige Phase restlos verfestigt ist, ist die Zusammensetzung natürlich (im Mittel oder global) diesselbe wie in der flüssigen Phase. Aber ist das Gußstück oder der Kristall homogen? Ist die Zusammensetzung überall dieselbe?
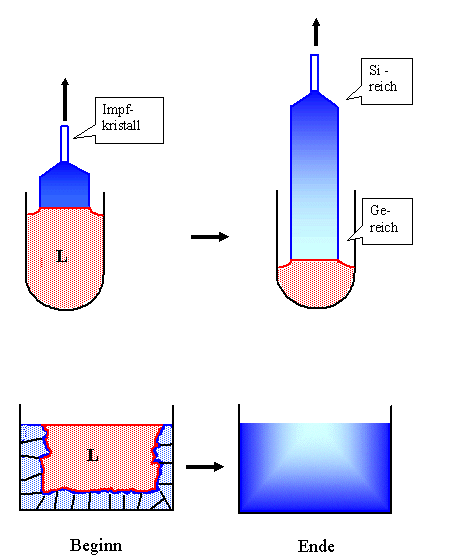
	Wenn wir nicht genügend Zeit geben, um den zuerst erstarrten Bereichen zu erlauben, ihre Zusammsetzung durch Diffusion in den neuen Gleichgewichtszustand zu bringen, werden wir einen Kristall (oder einen Gußkörper) bekommen, bei dem die zuerst erstarrten Teile (der obere Teil des Kristalls oder die Außenseite des Gußkörpers) Si-reich sind, der untere Teil des Kristalls oder das Innere des Gußkörpers) sind dafür Ge-reich. Fast nirgends hat der Festkörper die Zusammensetzung c0.
		Denn jedesmal wenn wir jetzt die Temperatur etwas erniedrigen, starten wir mit einer anderen Zusammensetzung der Schmelze, als es dem Gleichgewichtsfall entspräche; wir bleiben nicht auf einer Isoplethe im Phasendiagramm.
	Das bedeutet, daß wir gar nicht mehr die Zusammensetzung c0 in der flüssigen Phase haben.
		Im nächsten Schritt müssen wir also untersuchen was passiert, wenn bei einer weiteren kleinen Temperaturerniedrigung von T1 nach T2 jetzt eine Schmelze zur Zusammensetzung cL1 kristallisiert.
		Das Ergebnis ist klar: Beide Konzentrationen verschieben sich in Richtung Ge-reich. Unser Endprodukt sieht schematisch so aus wie in der folgenden Graphik gezeigt.

	Die Konsequenzen dieses Verhaltens beim Erstarren sind weitreichend:
		Auf der negativen Seite vermerken wir, daß es offensichtlich schwierig sein kann, eine homogene Legierung mit einer festen und überall konstanten Zusammensetzung zu gießen oder einen homogenen Kristall zu ziehen. Die Gußtechnik, nach wie vor das Arbeitspferd der gesamten Metallindustrie, ist nicht so simpel wie man glauben könnte!
		Auf der positiven Seite ist zu konstatieren, daß man durch diesen Effekt Materialien auch reinigen kann. Gerade bei Si und Ge wird eine leicht verunreinigte Schmelze oft so erstarren, daß zunächst nur eine Si- bzw. Ge - reiche a - Phase entsteht, d.h. ein saubereres Material. Die Verunreinigungsatome bleiben zunächst in der Schmelze.
		Diese Technik ist unter dem Namen "Zonenreinigen" oder "Zonenschmelzen" bekannt und hat in den frühen Jahren der Halbleiterindustrie eine wichtige Rolle gespielt.
	Damit ist aber nur eine Komplikation zum Thema "Gießen" angesprochen. Ein weiteres Beispiel dazu, wie kompliziert das simple "Gießen" sein kann findet sich in diesem (relativen) Link (mit Dank an Bob Rapp und "Materials Today" für die Genehmigung der Verwendung an dieser Stelle; hier der absolute Link zum Original).
	Als nächstes wollen wir nun im folgenden Unterkapitel ein etwas komplizierteres Phasendiagramm betrachten.

© H. Föll (MaWi 1 Skript)