|
Betrachten wir zunächst das einfachste der "komplizierten" Phasendiagramme:
Zwei Substanzen A und B mit einer Mischungslücke
, die auch nicht miteinander reagieren, d.h. keine Verbindungen der Form Ax By formen.
Ein gutes Beispiel ist Lötzinn , das System Sn - Pb. |
|
 |
Mischungslücke
heißt, dass in einem bestimmten Bereich der Zusammensetzung sich A und B nicht mischen, d.h.
keinen Mischkristall bilden. Wir haben dann eine Mischphase vorliegen, ein Gemenge aus den
Phasen a + b |
|
 |
Wir nennen die Phasen absichtlich a und b,
und nicht etwa A und B . Denn
a und b sind eben nicht z.B. Körner aus
reinem
A bzw. B, sondern Körner aus hauptsächlich A, die aber noch bis zur Löslichkeitsgrenze
B enthalten bzw. B mit gelöstem A, eben a + b
. |
|
 |
Grundsätzlich kann man das Phasendiagramm für diesen Fall genauso aus freien Enthalpiebetrachtungen
ableiten wie bereits geschehen; dies wird in einem "Advanced"
Modul noch etwas näher erläutert. |
 |
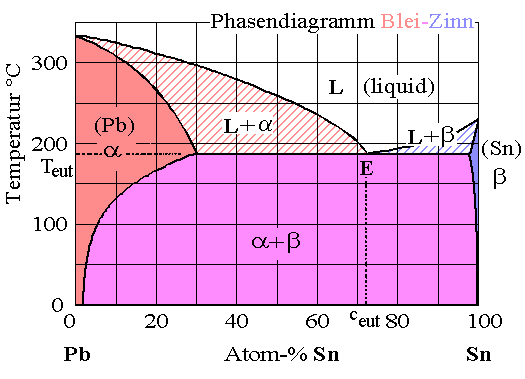
Das Phasendiagramm ist im folgenden Bild gezeigt |
| |
|
 |
Zunächst erkennnen wir die Phasen a = [Pb
mit einer relativ großen Menge an gelöstem Sn], maximal 19 Gewichts % oder 30 Vol.
%, und b = [Sn mit einer kleinen Menge am gelöstem Pb], maximal 2,5
Gewichts %. |
|
 |
Die beiden Kurven, die diese Phasen bis zum Maximalwert von der anderen festen
Phase a + b trennen, sind nichts anderes als die Löslichkeitskurven
der atomaren Fehlstellen ( Sn in Pb bzw. Pb in Sn) in der Phasendiagrammdarstellung. |
|
 |
Daß die Löslichkeit der jeweiligen atomaren Fehlstelle oberhalb der charakteristischen
Temperatur Teut wieder abzunehmen scheint, hat einen anderen Grund: Die Phase schmilzt, bevor die
maximale Löslichkeit erreicht ist. |
 |
Auch der Bereich a + b
ist klar. Wir haben ein
instabiles Zweiphasengebiet. In diesem Bereich wird jede Mischung in die nebeneinander
und gleichzeitig vorliegenden Phasen
a und b "zerfallen". Es gilt das Hebelgesetz für die relativen Anteile der beiden Phasen.
Dass jetzt beide Phasen fest sind, ist dabei unerheblich. |
|
 |
Wenn wir das Gefüge
des Festkörpers anschauen, finden wir a und
b Bereiche, d.h. fast reines Sn und relativ reines Pb, in irgendeiner Anordnung
vermischt. |
 |
Die beiden "Hörner" sind uns
auch schon bekannt: Hier liegt eine Mischung
fest - flüssig vor, genau wie im Beispiel des Si
- Ge Systems des vorhergehenden Unterkapitels. Hier können wir auch verstehen, was ein fest - flüssig Gemisch
in der Realität bedeutet. |
|
 |
Jeder, der schon mal gelötet hat, weiß, daß bei zu tiefen Temperaturen "
kalte" Lötstellen auftreten. Das Lötzinn scheint nicht richtig flüssig
zu sein, sondern hat eine breiige Konsistenz. Das ist genau die L + a
Phase des Phasendiagramms. |
|
 |
In einer Sn - reichen Flüßigkeit schwimmen Pb - reiche feste Kristalle,
oder, mehr wahrscheinlich, die kältere Außenseite ist fest und Pb - reich, die Innenseite ist flüssig
und Sn - reich. |
 |
Um zu sehen, was in diesem Phasendiagramm möglich ist, betrachten wir, was
geschieht, wenn wir von einer gegebenen Zusammensetzung (z. B. einer Pb reichen
Schmelze) ausgehen und abkühlen. |
|
 |
Solange wir oberhalb der durch die eutektischen
Temperatur Teut definierten Linie bleiben, wird sich das System in eine
feste
, Pb - reiche, und eine flüssige, Sn - reiche Phase aufspalten. |
|
 |
Starten wir von der Sn - reichen Seite aus, ist die Lage entsprechend. |
 |
Bei einer bestimmten Zusammensetzung, gegeben durch eutektische
Konzentration ceut
(die Konzentration am Punkt E), findet jedoch keine
Aufspaltung statt. Hier erfolgt ein direkter Übergang vom flüssigen in
den festen Zustand, es erfolgt die die eutektische Reaktion |
| |
|
| | |
|  |
Nochmals: Bei ceut haben wir einen
direkten Übergang vom Liquidus zu zwei festen
Phasen. Das hat, sofort erkennbar, erhebliche technische Bedeutung! |
|
 |
Allein schon die Bedingung der Nichtmischbarkeit erfordert
eine solche Reaktion, denn bei irgendeiner Konzentration der Flüßigphase müssen sich die beiden fest - flüssig
Phasengebiete L + a und L + b ja mal
treffen. |
| | |
|
 |
Am dadurch definierten und ziemlich häufig erscheinenden
eutektischen Punkt sind notwendigerweise 3 Phasen miteinander im Gleichgewicht:
L, a und b. |
|
|
 |
Die Phasenregel erlaubt damit
keinen Freiheitsgrad mehr;
Temperatur und Zusammensetzung
aller Phasen sind festgelegt; siehe die Graphik |
|  |
Die zwei festen Phasen a und b
in ihrer jeweiligen Zusammensetzung müssen also notwendigerweise durch eine
Linie mit konst. Temperatur verbunden sein, damit ist die allg. Struktur des Phasendiagramms
klar. |
|
 |
Daß der eutektische " Punkt"
im Phasendiagramm als "Linie " erscheint, ist zwar etwas verwirrend, aber
in Bezug auf die Temperatur ist es trotzdem ein Punkt. Und nur darauf kommt es an |
|
| |
| |
 |
Was bedeutet das hübsche Wort " Eutektikum"?
Es ist griechisch und heißt " gut schmelzend" oder auch "schön
gefügt; wohl aufgebaut". Denn die eutektische Zusammensetzung einer Zweistoffmischung oder Legierung hat zwei
bemerkenswerte Eigenschaften: |
| |
|
 |
1. Die eutektische Zusammensetzung schmilzt komplett bei der
tiefstmöglichen Temperatur. | |
|
|
 |
2. Die Schmelze erstarrt direkt
, ohne sich vorher in zwei Phasen zu zerlegen, wieder in die eutektische Zusammensetzung. Wir müssen also ein Eutektikum zweier Stoffe nicht g
a n z l a n g s a m abkühlen, um die Zusammensetzung halbwegs homogen zu halten, sondern können
so schnell abkühlen wie wir wollen. Wie so was aussehen kann ist rechts gezeigt. Wir haben ziemlich ordentliche "schön
gefügte" Lamellen aus abwechselnd Pb und Sn . | |
|  |
Sicherlich wird das Gefüge von der Abkühltemperatur abhängen, aber die zuletzt erstarrten
Gebiete haben dieselbe generelle Zusammensetzung wie die zuerst erstarrten. | |
| | | |
|
 |
Die eutektische Reaktion L ®
a + b ist eine der sogenannten
invarianten Reaktionen
die in Zweistoffsystemen ablaufen können. Dabei entsteht aus zwei Phasen
eine dritte Phase bzw., in der Rückwärtsreaktion wie oben notiert, entstehen
zwei Phasen aus einer Phase. |
|
 |
Invariant, heißen diese Reaktionen deshalb, weil nach der Phasenregel keine Freiheitsgrade
mehr existieren, d.h. Temperatur und Zusammensetzung sind unveränderlich
festgelegt, sie sind invariant, eben nicht mehr variant = variabel |
|
 |
Dabei sind dann auch noch weitere Phasen, z.B Verbindungen der Form AxB
y zugelassen. |
 |
Wir wollen hier aber nicht mehr weiter in die Systematik der Phasendiagramme eindringen, sondern
zum Abschluß und zur Illustration des bisher Gelernten, noch ein wirklich kompliziertes Phasendiagramm diskutieren.
Damit kommen wir zum letzten Unterkapitel des Generalthemas "Gleichgewichte". |
© H. Föll (MaWi 1 Skript)