|
Ein Teilchen, oder auch ein ganzes System von Teilchen, befindet sich im Gleichgewicht, falls sich "nichts" mehr ändert. |
|
|
|
 |
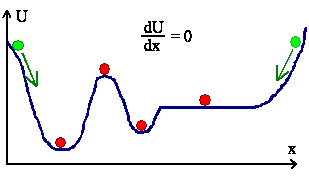
Bei einem klassischen "System" aus nur einem Teilchen ("Massenpunkt")
herrscht Gleichgewicht, falls sich das Teilchen im Minimum der potentiellen Energie befindet und jede Bewegung durch Reibung
beendet ist. | |
|
 |
"Treibende Kraft" in Richtung Gleichgewicht
ist dabei die Minimierung der Energie. | |
| | |
| |
 |
Systeme vieler miteinander wechselwirkender
mikroskopischer Teilchen müssen durch geeignete makroskopische (meßbare) Größen oder Zustandsvariablen
beschrieben werden, die das System hinreichend charakterisieren. | |
Zustandsvariable sind beispielsweise:
- Temperatur
- Druck
- Teilchenzahl
|
|
|
 |
Im umfassenden thermodynamischen Gleichgewicht ändern
sich diese Zustandsvariablen nicht mehr. |
|
|
 |
Treibende Kraft in Richtung Gleichgewicht ist nicht nur die Minimierung der Energie, sondern
auch die Maximierung von "Unordnung". | |
| | |
| |
 |
Thermisches Gleichgewicht bedingt dieselbe
Temperatur T, mechanisches Gleichgewicht denselben Druck p
überall im System. | |
Mechanisches und
thermisches und
chemisches Gleichgewicht
= thermodynamisches Gleichgewicht
|
|
 |
Chemisches Gleichgewicht bedeutet, dass sich
die Teilchenzahlen ni nicht mehr ändern. |
|
|
 |
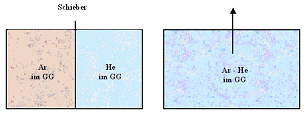
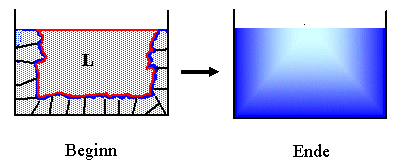
Beispiele:
- Zwei Gase mischen sich bis die (mittlere) Teilchenzahl überall dieselbe ist.
- Salz löst sich in Wasser - bis "Sättigung", d.h. chemisches Gleichgewicht erreicht ist. Die Zahl
der gelösten Ionen ändert sich nicht mehr.
|
|
|
 |
Ein "Teilchen" kann dabei vielerlei sein, z.B. ein Atom, Ion oder Molekül;
aber auch ein Elektron, Photonen, Phonon, Defektelektron (= "Loch"), usw. |
|
 |
Der Begriff chemisches Gleichgewicht ist deshalb
etwas mißdeutig; besser wäre "Teilchenzahlgleichgewicht". |
| |
| | |
| |
 |
Was wir brauchen ist ein thermodynamisches Potential
F = F(Zustandsvariablen) in Analogie zum rein mechanischen Potential. |
|
Gleichgewichtsbedingung für thermodynamisches Gleichgewicht:
| DF | = |
¶F
¶n1 |
· Dn1 + |
¶F
¶n2 |
· Dn2 + |
¶F
¶n2 |
· Dn3 + ..... |
= 0 |
|
|
|
 |
Thermodynamisches Gleichgewicht liegt dann vor, falls F ein Minimum hat |
|
|
| |
| |
 |
Das Gleichgewicht in einem Systeme vieler Teilchen ist ein dynamisches
Gleichgewicht. | |
|
|
 |
Nur makroskopisch ändert sich nichts, mikroskopisch
kann es trotzdem große Änderungen geben, die sich aber (im Mittel) exakt kompensieren. |
|
|
 |
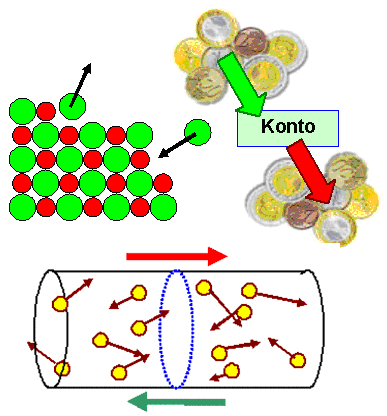
Beispiele: - Salzauflösung: Zahl der Na+
Ionen die in Lösung gehen = Zahl der Na+ Ionen, die sich am Kristall binden.
- Girokonto: Abhebungen = Einzahlungen.
- Strom: Elektronenfluß nach rechts = Elektronenfluß nach links.
|
|
 |
Der 1. Hauptsatz der Thermodynamik ist der Energieerhaltungssatz
inklusive der Wärme Q als Energieform. | |
|
|
 |
In differentieller Form besagt er, dass die Änderung der inneren Energie
U des betrachteten Systems gleich ist der (differentiellen) zugeführten Wärme Q abzüglich
der nach außen geleisteten (differentiellen) Arbeit W. |
|
|
| |
| |
 |
Atomistisch betrachtet bestehen alle Systeme aus Teilchen; thermodynamische Parameter
oder Zustandsvariable wie Druck und Temperatur
entstehen aus statistischen Betrachtungen von Teilcheneigenschaften. |
|
|
|
 |
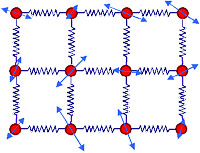
Die innere Energie ist nichts weiter als die in den energetischen Freiheitsgraden
f residierende kinetische und potentielle Energie. |
|
|
 |
Freiheitsgrade für kinetische Energie sind z.B. die Translation, Vibrationen, Rotationen. |
|
|
| |
| |
 |
Die Fundamentalformel, die die Temperatur T auf ein Maß für
die innere Energie U zurückführt lautet: | |
|
| |
| |
|
 |
Führt man bei konstantem Druck nur Wärme
dQ zu, wird trotzdem Arbeit durch die Volumenausdehnung dV geleistet. |
|
|
| |
| |
 |
Da bei Festkörpern i.d.R. die Bedingung konstanter Druck vorliegt, und die
Effekte der Wärmeausdehnug meist nicht interessieren, führt man als Maß für die innere Energie eine
neue Größe ein, die Enthalpie H. |
|
|
|
 |
Damit gilt sehr einfach dH = dQ. |
|
| |
| |
|
 |
Eine erste sehr weitreichende Konsequenz ergibt sich für die spezifischen
Wärmen c aller Materialien. | |
| cKrist, mol |
= cp, mol = |
½ · 6 · R = 3R |
|
|
|
 |
Insbesondere für Festkörper / Kristalle muß gelten, dass sie alle dieselbe konstante molare spezifische Wärme R (=Gaskonstante) haben müssen. | |
|
 |
Experimentell ist das nur für "hohe" Temperaturen erfüllt. Dieses, in
der klassischen Physik unlösbare Dilemma, wird erst durch die Quantentheorie beseitigt. |
|
| |
| |
|
 |
Der 1. Hauptsatz verlangt nur die Erhaltung der Energie, d.h. verbietet
ein Perpetuum mobile 1. Art. | |
|
|
 |
Er verbietet aber z.B. nicht, dass Arbeit nach außen geleistet wird, indem sich das
System abkühlt (–dQ); d.h. erlaubt ein Perpetuum mobile 2. Art. |
| |
|
 |
Das ist nicht in Einklang mit dem Experiment - wir brauchen einen 2. Haupsatz, der
ein Perpetuum mobile 2. Art ausschließt. |
| |
| | |
| |
 |
Naturgesetz: Von allen nach dem 1. Hauptsatz erlaubten Makrozuständen sind im thermodynamischen Gleichgewicht
immer nur die "unordentlichsten" realisiert. |
|
F = U – T · S
G = H – T · S |
|
|
 |
Als quantitatives Maß für die Unordnung in einem System wird die Entropie S definiert. |
|
|
 |
Naturgesetz: Mit zunehmender Temperatur nimmt die Unordnung und damit S
zu. | |
 |
Die beiden "Naturgesetze" lasssen sich durch die Definition von thermodynamischen Potentialen zusammenfassen und quantifizieren. Gleichgewicht liegt vor, falls
das passende Potential ein Minimum hat. | |
|
 |
Die freie Energie F beschreibt den Fall konstanten Volumens. |
| |
|
 |
Die freie Enthapie G beschreibt den Fall konstanten Drucks und ist dshalb für
Festkörper wichtig. | |
|
 |
Für spontan (= in Richtung Gleichgewicht vorwärts
in der Zeit) ablaufende Vorgänge gilt: | |
| dG(ni, T, ..) = |
| |
S
i |
¶G
¶ni |
· dni + |
¶G
¶T |
· dT + .... < 0 |
|
|
|
 |
Im Gleichgewicht ist dG = 0. |
|
|
 |
Dies ist die einzige Grundgleichung der Physik, die eine Richtung
der Zeit enthält! | |
| | |
| |
|
 |
Fast immer gelten gleichzeitig Nebenbedingungen, die berücksichtigt werden
müssen. | |
| NaCl | Û |
Na+ + Cl– |
| | | | dnNaCl |
= |
– dnNa = – dnCl |
|
|
|
 |
Beispiel: Die Auflösung von Salz in Wasser hat als
Nebenbedingung eine Verknüpfung der Zahl an Na+, Cl– und NaCl Teilchen. |
|
| |
| |
|
 |
Die partielle Ableitung ¶G/ ¶ni
eines thermodyamischen Potentials nach einer Teilchenzahl heißt das chemische Potential
µi des betreffenden Teilchens Nr. i. |
|
¶G
¶ni |
= µi = chem. Potential |
|
|
|
 |
Die Gleichgewichtsbedingung mit Hilfe eines thermodynamischen Potentials erlaubt sofort ein
tiefes Verständnis von temperaturgetriebenen Vorgängen (z,.B. Gefrieren / Schmelzen); auch schon ohne quantitative
Defintion der Entropie. | |
| |
| |
 |
Die Entropie eines Makrozustandes kann dann als Wahrscheinlichkeit des Vorliegens
dieses Makrozustands angesehen bzw. sogar definiert werden. | |
 |
 |
Makrozustand
"geordneter Kristall"
p = 1 | Makrozustand
"ungeordneter Kristall"
p = sehr groß |
|
|
 |
Zur Berechnung der Entropie S müssen wir "nur" die Zahl der der
möglichen Mikrozustände
pi wissen, mit denen sich der Makrozustand Nr. i realisieren läßt. |
|
|
 |
Beispiel: n Leerstellen in Kristall mit N Atomen definiert Makrozustand. Zahl Anordnungsmöglichkeiten = Zahl Mikrozustände. |
|
|
| |
| |
 |
Die Entropie ist dann durch die nebenstehende "Boltzmannformel" definiert. |
|
|
|
 |
Man kann statt pi auch dieWahrscheinlichkeit
wi = pi / Spi
eines Zustandes nehmen, das verschiebt jedoch nur den unbestimmten Nullpunkt der Skala. |
|
|
| |
| |
 |
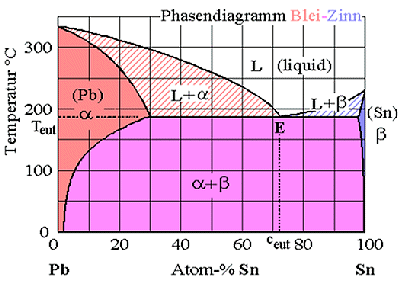
Ein Phasendiagramm gibt für jeden Punkt im Temperatur - Zusammensetzungsdiagramm
an, welche Phase oder Phasen im Gleichgewicht vorliegen |
|
|
|
 |
Zwischen der Zahl der Komponenten C (hier Pb und Sn),
die Zahl der Phasen P die vorliegen, und der Zahl F der Freiheitsgrade (hier Temperatur und
Komposition) die möglich sind besteht eine fundamentale Beziehung, die Gibbsche Phasenregel |
|
|
| |
|
|
|
| |
|
| |
|
|
 |
Für ein binäres Phasendiagramm (d.h. C
= 2) und zwei Freiheitsgrade f = 2 gibt es dann nur eine
mögliche Phase. | |
| | |
| |
|
 |
Zwei-Phasen Gebiete oder Mischphasen
im Phasendiagramm bestehen deshalb immer aus Phasen fester Komposition: a + b,
L + a, oder L + b). |
|
|
|
 |
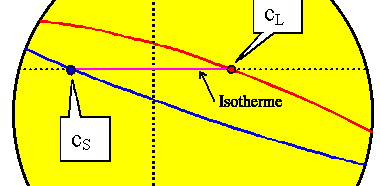
Die beiden Kompositionen ergeben sich aus den Schnittpunkten der Isotherme
mit den das Mischphasengebiet begrenzenden Linien. | |
|
 |
Der jeweilige Anteil fa und fb der beiden Phasen ergibt sich aus dem Hebelgesetz |
|
|
| |
|
|
|
| |
|
| |
| |
 |
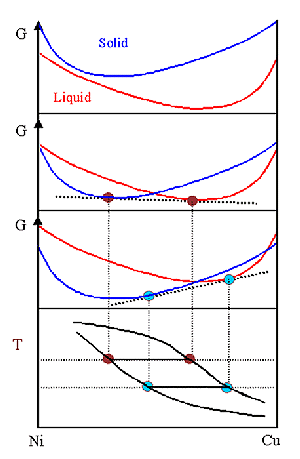
Phasendiagramme erhält man durch Vergleich der freien Enthalpien möglicher
konkurrierende Phasen. | |
|
|
 |
Qualitativ relativ einfach, quantitativ aber schwer. |
|
|
 |
Unmittelbare Konsequenz: Es gibt keine einfachen Phasendiagramme - Mischphasen sind häufig. |
|
 |
Bei Eutektika gibt es einen Punkt (T,
C, d.h. f = 0), in dem drei Phasen (L = flüssig + feste a
und b) im Gleichgewicht stehen |
|
|
 |
Im obersten Bild gibt der Punkt "E" die eutektische Komposition, die waagrechte
Linie die eutektische Temperatur. | |
|
 |
Die zugehörige invariante Reaktion (invariant = keineFreiheitsgrade)
lautet | |
|
| |
|
|
|
| |
|
| |
|
|
 |
Weiter invariante Reaktionen führen zu peritektischen, eutektoiden und peritektoiden
Typen von Phasendiagrammen. | |
| | |
| |
 |
Bei gegebener Komposition und Phasendiagramm lassen sich weitreichende Schlüsse
auf das zu erwartende Gefüge ziehen. |
|
|
|
 |
Insbesondere wird unmittelbar klar, daß eine homogene einphasige Schmelze nach dem Erstarren
i.a. keine homogene Zusammensetzung mehr haben wird. | |
|
 |
Ausnahme: Invariante Reaktion, d.h. eutektische Komposition. |
|
 |
Bei vermeintlich einfachen Techniken wie Gießen, Schweißen oder Kristallziehen,
laufen in Wahrheit komplexe Vorgänge ab. | |
|
 |
Die unmittlbare Anwendungen dieser Verfahren ist oft nicht möglich oder bedarf erheblicher
"Tricks". | |
| | |
| |
|
| |
|
|
| | |
| |
|
© H. Föll (MaWi 1 Skript)