8.3.1 Forming your Battle Line: Solid Solution and Precipitation Hardening.

8.3 Hardening Steel - the First

8.3.1 Forming your Battle Line: Solid Solution and Precipitation Hardening.

The Cost Issue

We are there. Finally! From now on we will only deal with steel because you now have amost of the major tools in your possession that we shall need for hardening steel.
Thank God, I don't have to tell you anymore that hardening means to increase the hardness, and that this is the same as raising the yield stress. You also know how the yield stress is defined, how it is measured in a tensile test, and that it is just a measure for how easy or difficult it is to move dislocations. You know what a dislocation is, and how its movement induces plastic deformation.
That's why from now on I won't make links anymore whenever terms like those are coming up.

We start with solid solution and precipitation hardening of iron and steel. We have more or less covered that topic already; look up some old figures. This link beautifully illustrates what we are discussing in the context of battling dislocation movement.

What we have seen in the aluminum - copper case is that single atoms of copper in aluminum are more effective at obstructing dislocation movement than very small precipitates of copper atoms.
Large precipitates are inefficient too, because you can only have a few of those. So there is some optimal combination of size and number; the Al-Cu system nicely illustrated that.

The aluminium - copper system also demonstrated that the strategy derived from "theory" works well. Should we now use the same strategy with steel? Find the best element to alloy iron with and then get going?

No, we shouldn't. There are several problems. One is particular virulent for modern smiths (or engineers, as we call them now). It's called: money. About the others we shall see shortly.

The money problem is simple and obvious. In our fast-living, sometimes enlightened, but always cheap age, you, the modern engineer, just do not have all the time and the money in the world to make your steel and work with it. Costs matter. Very much so.

Cars would not be affordable for the likes of me and possibly you, if car bodies still would have to be made like a old-fashioned sword or a suit of armor. Those were expensive items in their ages that only people could afford who were quite rich. Richness then mostly came from robbing your serfs and underlings - at sword point, if necessary. Let's be happy that in our enlightened times the ~~politicians bankers~~ robbers usually don't have swords.
If costs matter we must compromise. Quite a lot actually, if we want to produce large amounts of cheap steel. We now run into the eternal conflict between the great things one could do in principle, and the things that eventually will make money. Let's call that the great cost issue .

By the way, we are going through that stage right now with solar cells. We know exactly how to make superior solar cells if money and time doesn't matter. If it does, and for solar energy it most certainly does, we must and will compromise. There are a lot of parallels between the development of mass -produced cheap but still good steel after about 1850, and what's going on right now about mass-producing cheap but good silicon for solar cell production.
I wrote that around 2012. I'm happy to report that solar cells are now (beginning of 2015) cheap enough to make it on their own, without subsidies, on a highly competitive energy market. And they will et cheaper and better in years to come - just like steel about 150 years ago.

Advanced
Module

Solar Cells

But back to steel. We could make superior steel by starting with very pure iron and alloy it with the whatever is best for making extremely hard but still very tough steel. We actually do to some extent!
We alloy our top steels with several elemtnts in just the righ amounts and use optimized temperature profiles to produce the best possible combination of precipitate type, size and concentration. The principles are the same as the Al - Cu example but the reality is far more complex.

What you might get is, for example, "maraging" steel. As suspected before, it actually does not use carbon as the key element for hardening, but you don't have to worry about that - most of us couldn't afford maraging steel for car bodies or other bulk uses. I will come back to maraging steel later and then also explain the meaning of the term "maraging".

Taking the great cost issue into account we must try to live with rather dirty iron, and with carbon as the major alloying element.
That's more or less what you, the ancient smith, had to content with anyway, even so you didn't know about that. The "more or less" refers to a facet of steel lore that I have not yet mentioned but saved for now:

A lot of ancient steel contained phosphorous (P) and not carbon (C)
as the major alloying element.

I'll get to this in due time. For now let's concentrate on the dirty iron - carbon system. Whenever possible we even ignore the dirt. If it is not possible, I will tell you.

Solid Solution Hardening in Iron

First let's look at solid solution hardening, or hardening with atomically dissolved impurity atoms. In order to get clean data, we need to do this in a lab-type experiment, paying no attention to the cost issue.

What exactly are the effects we can get with carbon or other elements that are being kept in solid solution inside an iron crystal with respect to hardness and so on? Here are some data for iron and for comparison for really soft copper (Cu):


Solid solution hardening in ferrite. High concentrations of dissolved C, N and P are not possible. All curves would converge around 25 MPa for zero concentration, showing that pure iron is very soft.

Solid solution hardening in copper. Note the difference in scales! R_P, you remember, is the critical yield strength and more or less the same as hardness

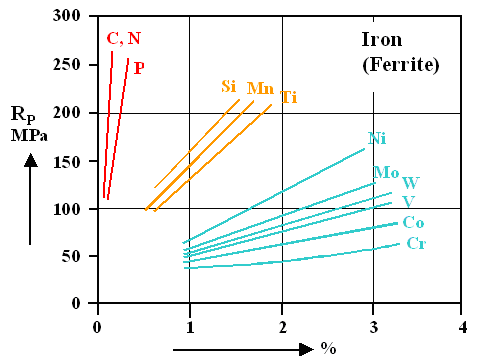
	The curves always refer to the best we can do with pure iron or pure ferrite, as we now always call the room temperature bcc crystal. Now you see the other problems besides the cost issue alluded to above. There is a definite hardening effect for all the impurity elements shown. But what we get in all cases is still rather soft ferrite. Look at the Al-Cu system again for comparison. There we got a maxuimum yield stress (R_P) of about 350 MPa (Mega Pascal; last time I remind you about that!) for Cu-precipitate hardened Al. Even the softest version of our Al-Cu system with about 150 MPa is about as hard as most iron-impurity systems in the picture above. When we talk about hard steel, we talk about at least 500 MPa. The "best " elements for solid solution hardening are the interstitials: carbon (C) and nitrogen (N) plus substitutional phosphorous (P). So why don't we increase their concentrations, extending the curves to larger yield stress R_P or hardness values? Because the phase diagrams tells you that you cannot keep larger concentrations in solid solution at room temperature. We already know that for carbon (this link gets you there); more than about 0,1 % at high temperature can't be done. For the date in the figure above thus a few tricks had to be used to keep the atoms in solid solution. That's also true for nitrogen and phosphorous; look it up yourself. The substitutional atoms like Silicon, (Si), nickel (Ni) and so on don't help much either. For a yield stress of 500 MPa you would need rather high concentrations and it is not so likely that you can keep high concentrations in solid solution. Just check the phase diagrams. If we use dirty iron as we must, e.g. iron with some carbon and some of the other elements, all kinds of other things can happen. We cannot simply add the effects of different atoms. In other words: putting in, for example, 1 % silicon (Si) and 1 % molybdenum (Mo) will not necessarily give you a yield strength of about 300 MPa. It might be even worse than it is for just one of these elements.
		By the way, the curves above are based on 11 different phase diagrams, as you must have noticed. It makes no sense to ask our graduate students to make a sample of iron with x % of some impurity in solid solution, if the phase diagram tells you that it can't be done. I do hope that you appreciate that those simple looking curves above are based on a hell of a lot of work. What you learn is that carbon is indeed the most efficient single mercenary that you can field in the fight against moving dislocations, but that it will not do you much good. The first law of applied science asserts itself once more.
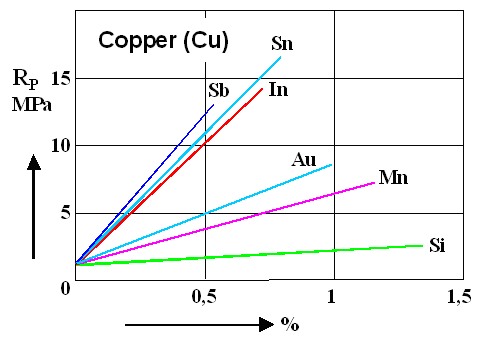
		The figure on the bottom, just for the hell of it, shows exactly the same thing for copper (Cu). I spare you the rest of the metals but rest assured that there is a lot of data. What you learn is that pure copper is rather soft, indeed, in comparison to pure iron (look at the numbers on the scale!) and that you can harden it quite a bit with half a percent or so of antimony (Sb), tin (Sn) or indium (In). Nevertheless, it is still rather soft. Tinkering in your garage with the goal of making a copper (alloy) sword with a yield stress of 500 MPa or so, thus will be foolish. There is nothing more practical than a good theory! Note that Silicon (Si), doing not too badly in iron, has almost no effect in copper.

Precipitation Hardening in Iron

How about a lot of carbon in iron. Far more than the solubility limit in ferrite or a-phase at room temperature? Than the system will produce cementite precipitates and we can go for precipitation hardening.

Yes—but! We know that as long as we cool down slowly enough, what we will find is:

ferrite + pearlite for hypoeutectoid compositions;
pearlite + cementite for hypereutectoid compositions.

No more links to what should be elementary stuff by now as I have promised or threatened, whatever it is to you. In case of doubt look it up via the index.

So, yes, the carbon beyond the solubility limit does precipitate and form cementite. However, it will not form a bunch of small and more or less spherical cementite particles as we would like it, but far more complex structures, especially for carbon concentrations > 0,7 %, i.e. hypereutectoid carbon steel.

In order to keep things simple, let's first look at hypoeutectoid steel with rather low carbon concentrations. That will span the range from wrought iron to mild steel.

Mild steel produced by cooling down no too fast must have a structure consisting of pure ferrite grains plus some pearlite grains, just as shown here. The ferrite grains will have dissolved as much carbon as possible (about 0,02 %) and thus have a yield stress around 200 MPa, as we can deduce from the picture above.
The pearlite grains are much harder since they contain cementite. Cementite is brittle at room temperature and thus impenetrable to dislocations. Dislocations may still move in the ferrite between the cementite lamellae but pearlite grains are a formidable obstacle to dislocation movement. They thus introduce a less ductile and more brittle component.
We can make an educated guess that an increasing carbon concentration (but still well below the eutectoid composition) will produce the following effects with increasing carbon concentration:

The yield strength will increase from a starting value of about 150 MPa to values far larger.
Ductility or the maximum elongation will go down.
The fracture energy will go down as well.
Closer to the eutectoid composition new things start to happen and these trends may change.

Now let's look at hypereutectoid steel.

That's simple. For carbon concentrations well above the eutectoid compositions and "normal" coolin we must expect that we have pearlite grains completely encased in primary cementite, just look at that fantastic picture again. In this case we expect a hard and completely brittle material.
If we are just a little bit above the eutectoid composition, some ductility might still be there.

What we get experimentally for plain carbon steel is shown below:

	$Carbon and the fracture properties of iron$
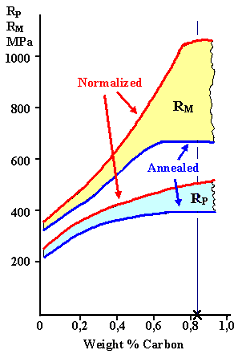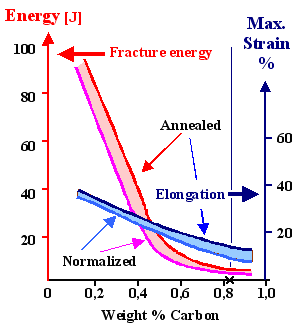Effect of carbon on steel properties. The vertical line at the cross marks the eutectoid composition
"Normalized" and "Annealed" refer to the starting structure. Yield stress R_P (and ultimate tensile strength R_M), fracture energy and ductility (maximum strain or elongation) behave pretty much as expected.

It is more or less what we expected. With increasing carbon concentration the yield strength goes up, the fracture energy down. No surprise here.

This trend, however, already weakens around 0,5 %, long before the eutectoid composition is reached. That is, perhaps, a bit surprising?
Well - no! Plastic deformation needs dislocations to run through the whole sample. This means that there must be a contiguous region of material from one end to the other through which dislocations can run. It is like electrical current. If you don't have a conducting path between two electrical terminals, no current will flow - no matter how much conducting materials, mixed up with isolating material is in between.

Let's visualize what is going to happen if we have two kinds of grains in some variable kind of proportion inside some material. One kind of grain is a "conductor" for electrical current or dislocations, the other one is an "isolator" - electrical charge or dislocations cannot move inside these grains. Highly stylized and for only 2 dimensions we get something like this:


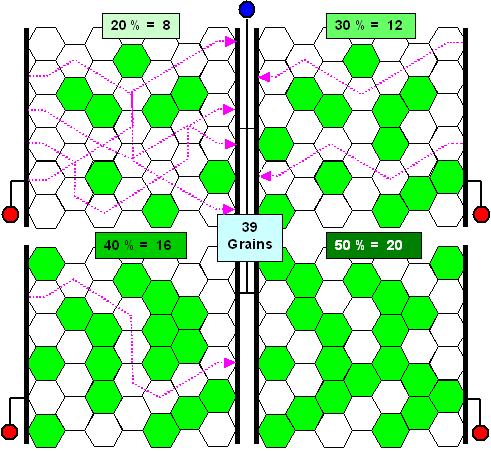Percolation of electrical current or dislocations through a mix of 39 grains. White ones are conducting and green ones are not

The hexagons symbolize grains. White ones can conduct electrical current or can be deformed plastically, i.e. dislocations in these grains are mobile. Ferrite, for example, can do both. Green grains are insulators and do not support dislocation movement. This would be the case for pure cementite. Pearlite, however, is still a good electrical conductor (because of the ferrite in there) but almost an insulator with respect to dislocation movement.
An electrical connection between left and right is shown symbolically, and the dotted purple arrows illustrate some of the possible pathways for electrons or dislocations that lead from left to right. The percentage of statistically distributed green grains increases from about 20 % to 50 % and it is immediately apparent, that at some critical percentage, no more flow or percolation of electrons or dislocations from left to right is possible.

The word percolation refers to the twisted step-by-step flow of whatever; you know that from the percolator that makes your coffee. Percolation science is more demanding than coffee making, however.

For example, if you extend the problem posed above to three dimension and ask at what percentage of statistically distributed insulating grains the mix switches from a conductor (at least one current path can still be found) to an insulator (no current paths' anymore), the answer is not easily calculated. It' happens when about 3/4 of your spheres are insulators.
If we take that as a rough guess for dislocation movement too, we expect that around 75 % of the eutectoid composition it is also all over for dislocation movement. In other words, around 0.75 · 0.8 % C=0.6 % C we expect that yield strength and fracture energy "bottom out", i.e. don't change much any more. That is rather what the curves above show you.

What we will get depends of course not only on the carbon concentration but also on the structure of the specimen before the tensile test was done. We have already learned that one and the same steel can have completely different properties depending on its history.

They only way to get comparable results is thus to first "anneal" or "normalize" the specimen. For today's steels you get precise instructions of how to do this. In essence you have to keep the steel at high temperatures for a time that is sufficient to achieve a state close to nirvana (done by annealing; takes a long times) or at least not too far off (normalizing; shorter time).

Now you know about solid solution and precipitation hardening of plain carbon steel. A bit disappointing, isn't it? We can get a yield stress of 500 MPa but for a high price: the material is also rather brittle.

For good swords we should be able to do better. So next we need to look at the remaining straight options for hardening steel.