3.1.4 A Bit More About Tensile Testing

We now give general or typical stress - strain curves of metals a closer look and define some terms. For that we look at the figure below. Let's go through major properties not yet discussed.


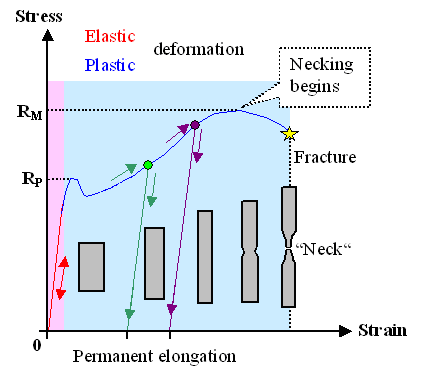Typical stress-strain curve for a metal and shape of the specimen. With this drawing I define the most important parameters.

All metals deform purely elastically for small enough stress. That's not surprising. It is exactly what you hope that your metal object—your sword, your car part, your fork, your elevator cable —will do when used. You don't want it to change its shape permanently.
You sure enough put stress on those parts when you use them, and you certainly assume that the engineers in charge of designing those objects knew how to make them in a way that they will only deform elastically under the various stresses you are going to challenge them with.
As far as sword forging goes, that is the key. As long as your sword only deforms elastically when you hit something with it, all is well. It will then neither come close to fracture, nor will it remain bend and out of shape. That is your the best option for sword behavior.

Alas! If you hit another good sword edge on edge, you get a lot of force on a small area, or a very high stress . You will quite definitely exceed any limits for elastic deformation locally. The only options left are fracture or plastic deformation.
Of course you go for the plastic deformation option: Suffering some plastic deformation locally is bad but far better than fracture. You have a local change of shape—a nick or dent—but still a usable sword.

Come to think of it, local plastic deformation is always a good option if the alternative is fracture. Run your car against a tree and you are much better off with just the front part dented than with everything broken.
I will get back to this later again because it is quite important.

If we go beyond the maximum stress for only elastic deformation, we will reach some special stress that is called the yield stress or the yield strength; often abbreviated R_P for historical reasons (we also have already used up the letter "Y" for Young's modulus).
As soon as the applied stress reaches the yield stress, the material starts to "yield", it starts to deform plastically . Up to this point it behaves purely elastically. This is important:

Plastic deformation begins as soon as
the yield stress
of a material is reached

Once again, because it is so important: Stress your materials but stay below the yield stress. It doesn't matter if you do this by pulling, pushing or any combination. Now release the stress and your material goes back to strain zero, assuming its old dimension.
That is the reason why ductile materials (and just about every material) can be assigned a Young's modulus.

After reaching the yield stress, further pulling (or pushing) will increase (or decrease) the length of ductile materials considerably. If you release the stress now (dashed blue lines in the figure above), the material shortens a little because the elastic part of the strain relaxes but it remains longer. It is now plastically deformed.

By the way:

What is commonly known as "hardness"
is nothing more than the yield stress,
just measured in different units.

There you have it. Expressions like "hard to deform" do make sense after all. Provided you mean "hard to deform plastically ". Here is a link illustrating this point with experimental results.
We will go into this in more detail later. What we note here is that hardening steel first and topmost means to increase its yield stress.

Put simply, you need more force or stress to plastically deform hard steel then you would need for mild or "soft" steel. It is harder to bend a paper clip made from hard steel into some strange shape than one made from soft copper. Note that the word hard appears here with two different meanings. It denotes the well-defined measurable quantity "hardness" and some feeling expressed in colloquial language.

I hope you got it that the sentence in the green box up there is nothing less than an epiphany or enlightenment! You now have a first idea about what hardness is in terms of materials properties. We will delve much deeper into the topic in chapters to come.

After I have written a lot of words about the critical yield stress, or "R_P", or hardness, we now move on to the next interesting feature of the stress - strain diagram. We note again that there is some maximum in the stress - strain curve that gives us the ultimate tensile strength usually abbreviated R_M.

More stress than that the material cannot take. If you apply more stress than R_M, the material would elongate quickly and break.
A well-programmed tensile test machine would never do that because it is keeping the strain rate constant, remember? After the strain going with R_M is reached, the machine needs to decrease the stress to increase the strain. That's why the curve has a downwards slope after R_M.

You might force the machine to apply a stress larger than the ultimate tensile strength, you're the boss, after all. You will then invariably produce a larger and larger strain rate, leading quickly to fracture.

Let's define some terms now.

The total change in length before fracture we call ductility. Ductility thus simply measures the maximum elongation in percent that you can get on top of the purely elastic deformation (always at best 0,1 % - 0,3 %).
Ductility typically will be between a few percent and a few ten percent for metals, but there are exceptions. Some metals—and wootz steel might be one of them—show the phenomena of super plasticity, exhibiting very large ductility up to or even above 100 % - at high temperatures, that is.

For reasons well understood the cylindrical rod we are pulling just gets uniformly longer and thinner while we increase the stress until we reach the ultimate tensile strength. If we keep pulling at the given constant strain rate (and for that the machine must actually release the stress a bit now), "necking" will start.
Necking in this case has nothing to do with what you and your girl friend might have done way back on the back seat of your Volkswagen. Here it simply means that a "neck" develops: the specimen gets locally thinner and thinner until it breaks at the thinnest part.

The stress - strain diagrams for all materials are hiding a last important property. It is the specific fracture energy, the amount of work = energy per cubic cm (J/cm³) you need to invest in you specimen so it finally breaks in a neat tensile test.
Oops! Sorry! The "J/cm³" or "Joules per cubic centimeter" right above just slipped in. Joules; abbreviated J, as I sincerely hope you know or at least knew, is the basic unit for energy. If electrical energy is involved, we also use the unit "Watt second " (Ws), and 1 Ws = 1 J. In case of doubt, look it up.
The fracture energy is simply given by ~~integrating the stress as a function of strain~~ - excuse me; I almost slipped into an equation involving the really dirty "i" word.
Let's try again: The specific fracture energy is simply given by the area under a stress-strain curve. This is illustrated below.


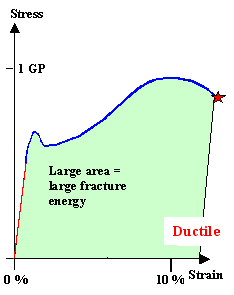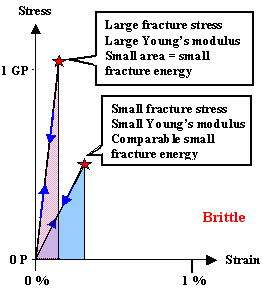
Fracture energy = area under the stress strain curve.
Brittle materials with large Young's modulus (steep slope) and large fracture stress do not necessarily have a higher fracture energy (area under the curve) compared to less stiff materials fracturing more easily	The fracture energy of ductile materials is always much larger than that of brittle materials. Note difference in scale

By the way, if you ever wondered what all that incomprehensible calculus, that sadistic math teachers forced on you in high school, is good for: stress-strain diagrams provide a good example.

The fracture energy is just the integral of the stress-strain curve taken from zero strain to the fracture strain.
Young's modulus results from taking the derivative of the curve at the elastic part for small stress.
The ultimate tensile strength is determined by setting the derivative of the curve to zero.
The tensile test machine knows how to do this. How about you?

Why are we interested in the fracture energy?

Because it is one of the reasons why you
may want to put "soft" steel
inside a hard steel sword blade

Whenever your sword hits something or gets hit, it has to absorb a certain amount of energy, possibly in a rather small area of impact and thus small volume.

If the energy deposited locally exceeds the specific fracture energy your sword breaks. It is (almost) as simple as that.

Nevertheless, I will not emphasize the specific fracture energy as derived from stress-strain curves too much. Why? Because it's a great number for characterizing nice uniform specimen in a nice careful test, but it doesn't do so well for messy real materials under violent ill-defined conditions.

When you hit another sword with your sword, or when King Richard (Lion Heart) cleaved the iron handle of a maze to demonstrate the quality of his sword to Sultan Saladin (here is where that particular myth comes from), the conditions are quite different from a neat tensile test with low strain rates. I will therefore give fracture a sub-chapter of its own.

But before I do this, we need to consider a few last points on tensile testing.

First, let's look at the strain rate a bit more closely. What you get in terms of the stress-strain curves depends on how fast you strain. Above a certain (rather low) strain rate, faster deformation always means that the material appears to be "harder".

If you hit your opponent's sword with your sword, the deformation on the swords, if there is any, will happen rather fast. That seems to be positive because the material appears harder, but there is always a price to pay. It's a good guess that during a short impact time you can't absorb as much energy as when you pull or press on your material slowly. So instead of having some deformation (which is bad) you might have fracture (which is far worse). So we must take strain rates into account when we look at sword blade properties.

Now a word to the opposite of the tensile test: compressive stress testing. Instead of pulling we push. We have compressive stress instead of tensile stress and now we compress the specimen until it fractures or, better word, bursts.

Compressive testing is a bit messy for large stresses because your specimen then will tend to bow. Press on your sword with the point fixed on the floor, and it will bow out elastically (we hope).
Apart from that, compressing the specimen means doing just the opposite of tensile testing. A ductile specimen under compressive load first deforms elastically with a stiffness given by the same Young's modulus you find on tensile loading.
After reaching the same yield strength as in tensile testing, it will begin to deform plastically. The stress strain-curve for not too large stress looks the same, just inverted, as in tensile testing. Well, no—only if you take a little care to adjust for the changed geometry.

Science
Link

Compressive test

For example the specimen gets thicker and not thinner and that needs corrections that involve logarithms and other hated math subjects, so I will not get into that. Look up the science module if you can bear the (simple) math.
If you do that and you know what happens for simple straight pulling, you also know what will happen for simple straight pushing .

Now comes a big theorem.

If you know what happens for
simple straight pulling, you can
calculate what will happen for
any mechanical loading

Pulling in one direction and pushing in another one, for example, bending, shearing or banging with a hammer, whatever. Concerning your job as smith for making swords, that is what you need. You never just "pull" at your sword; you rather bend it or suffer complex stress distributions in all directions if you hit something hard with the edge of the blade.

Note that I haven't said that those calculations are easy. They are not. Things like tensor calculus are involved, the same kind of math you need for Einstein's theory of general relativity, which isn't known for being particularly easy.

It's always good to have powerful theorems. It's even better to test them experimentally.
Given that real materials are never uniform, simple and well-behaved like "theoretical" materials, we don't just do tricky calculations and believe them unconditionally. We always measure major properties experimentally, and compare the measured values with the (needless to say, computer run) numerical calculations. "We", needless to say, means scientists and not, for example, economists or theologians, for comparison. They just believe, and that's why the economy (or moral rectitude) crashes far more often then structural designs like building, bridges, and so on.

When you, the ancient smith forges a sword blade, you apply stress in a complex way and consequently you deform the material in a complex way. You do not just elongate a cylindrical piece of iron like in a tensile test. When you work with your hammer, you rather are closer to pushing instead of pulling.

No matter. From the viewpoint of some tiny piece of iron inside the whole big piece you are about to crash you hammer down upon, it just feels some compressive stress; it is violently pushed down. It's neighbors are also pushed down to some extent, and all want to bulge out a bit to the sides. All those little connected pieces might feel different forces from the hammer, react to it, and pass on some stress to their neighbors.
The total effect is some total or global deformation resulting from the various local deformations of the connected pieces of iron. And all of that can be calculated if we know the data from the tensile test. The link tells more.

Science
Link

Deformation

The so-called "metal-bending industry", about the biggest industry we have, depends completely on the ability of some materials to be able to undergo plastic deformation.

Isn't it strange that until about 1934 nobody had the faintest notion of what exactly is going on inside a material when it deforms plastically ? Isn't it even stranger that hardly anybody knows the unsung heroes of science who unraveled the big mystery in 1934 and beyond?
The very persons whose ground-breaking work not only led the metal-bending industry to unprecedented progress but also opened the door for the electronic revolution?
Not to mention that based on their insights, we can now start to understand why the ancient smiths did what they did?

You get to meet some of those great people in the next chapters.