Heroes of Dislocation Science

	Heroes of Dislocation Science
	Here are some notes about some of the (early) "Heroes" of Dislocation Science. It is a purely subjective collection and does not pretend to do justice to the history of the field or the people involved. I will not even remotely try to establish a "ranking", and that's why names appear in alphabetical order.
	To put things in perspective, let's start with a short history of the invention of the dislocation, followed by their actual discovery.
		Dislocations were invented long before they were discovered. They came into being in 1934 by hard thinking and not by observation. As ever so often, three people came up with the concept independently and pretty much at the same time. The three inventors were Egon Orowan, Michael Polanyi and Geoffrey Taylor. What they invented was the edge dislocation; the general concept of dislocations had to wait a little longer. Of course, they all knew a few things that gave them the right idea. They knew about atoms and crystals since X-ray diffraction was already in place since 1912. They also knew that plastic deformation occurred by slip on special lattice planes if some shear stress was large enough, and they knew that the stress needed for slip was far lower than what one would need if complete planes would be slipping on top of each other.
		They were also aware of the work of others. Guys with big names then and still today, like T. v. Kármán, Jakow Iljitsch Frenkel, or Ludwig Prandtl, had put considerable effort into theories dealing, in modern parlor, with the collective movements of atoms in crystals. Markus Heyerhoff, in his PhD thesis from 1997 (University of Greifswald / Germany) has a lot to say about that and the rather fearsome equations that those guys dealt with. I must mention Ulrich Dehlinger in this context. Not only was he one of my Professors when I studied physics in Stuttgart / Germany, he almost "invented" the dislocation in 1929.
		This is a know phenomena in science. For every big breakthrough linked to one name (e.g. Albert Einstein) there are always some precursors that almost did it. For Einstein's special relativity theory, for example, we have Poincaré and Lorentz, rather well-known scientists then and now. Another known phenomena is that the acknowledged heroes usually didn't get it quite right or did not address important parts. For Einstein's special relativity theory once more, it was Minkowski who introduced the extremely innovative and elegant four-dimensional "space-time" concept that makes Einstein's stuff so much more powerful. We have the same thing here. While all the dislocation inventors supplied a drawing that shows a recognizable edge-dislocation (see below), some of their stuff is questionable or incomplete.
		Another known phenomena in science is that some mathematician or theoretician, for some obscure reason of his own, had already produced some framework for the big discovery yet to be made. In the case of dislocations it was Vito Volterra, who in 1905 provided just about everything needed to invent the dislocation.
		The last known phenomena in science is that some others, always including a least one major celebrity, bitterly oppose the new "invention" or insight. In the case of the dislocation, it was, for example, famous Frenkel. A more recent example can be found in this link.
	Nevertheless, the break-through made in 1934 was recognized by others, and the floodgates opened up for a deluge of research into dislocation science. New and important discoveries were made by many in a short time. I will only mention some of that, mostly because I don't know the details, and also because it would get too special and technical.
		Playing merrily with the new toy was spoiled on two points, however: The Nazis and the war made life difficult for many researchers in Germany and elsewhere. A lot were forced to emigrate, including Polanyi and Orowan. The rest couldn't do whatever they liked either. On the other hand, war-time necessities included improved metal techniques, and this lead to some special research that furthered the cause, e.g. in the context of the Liberty Ships. Nobody has ever seen a dislocation until 1955 / 56. To be sure, there was more and more experimental evidence, mostly from defect etching or similar techniques, that left no doubt that the concept was sound - but only seeing is believing!
		The first direct observation of a dislocation in a transmission electron microscope was thus of great importance. It also opened up the road to present-day micro- and nanotechnologies with an ever increasing arsenal of sophisticated analytical techniques.
	Some more details will be given in the short portraits that follow.

Johannes (Jan) Martinus Burgers

Everybody who knows the least thing about dislocations knows about the "Burgers vector" of dislocations. The Dutch scientist J.M. Burgers came up with this simple and powerful way to describe the "strength" and type of a dislocation.


Johannes (Jan) Martinus Burgers * January 13, 1895, Arnhem, Netherlands † June 7, 1981, Washington D.C.
Source: Wikipedia

He also is the "inventor" of the screw dislocation concept. Moreover, he was the first one to describe low-angle grain boundaries in terms of dislocation arrays.
His seminal contributions were published in 1939 in the "Proceedings of the Royal Soc. of Sciences" (Amsterdam).
In 1940 he published an influential summary of the state of the "dislocation" art in the Proceedings of the Physical Soc. in London.

It may thus come as a surprise (it certainly surprised me) that Jan Burgers was actually an authority on fluid dynamics for most of his life. He was dragged into the emerging dislocations science by his younger brother Wilhelm Gerard Burgers, a well-known metallurgist in his time, especially for his work about recrystallization.

It seems that the curls or eddies in fluids, entities well-known to Jan Burgers, inspired him to come up with the dislocation stuff that made him immortal for a long time to come. He was also the more mathematically inclined and more experienced of the two brothers at this time. After he made his contributions, he went back to fluid dynamics and never looked back.

And now you also know why dislocations have a Burgers vector and not a Burger's vector.

References:
Burgers, J, M., Proc. K. Akad. Wet. Amst., 42 (1939), p. 293 and 378 (2 contributions)
Burgers, J. M., "Geometrical considerations concerning the the structural irregularities to be assumed in a crystal", Proc. Phys. Soc. (London) 52 (1940) 23-33
Burgers, J. M., "How my brother and I became interested in dislocations", Proc. Phys. Soc. (London) A 371 (1980) 125-130
Parts of the content here comes from the excellent book of E.J. Mittemeijer.

Ulrich Dehlinger

Prof. Dr. Ulrich Dehlinger was one of my academic teachers in Stuttgart. He was an "original", noted for his many intentional and unintentional quips and wisecracks that invariably came up during his lecture courses. He was also feared by us undergraduates because the examination for his (required) "Technische Mechanik" lecture course was hard to pass.


Ulrich Dehlinger * June 6th, 1901; Ulm, Germany † June 29th, 1981, Stuttgart, Germany

Many years later I realized that his wisecracks, that we thought to be a bit offbeat and funny, were actually full of wisdom. After I became a professor myself, I also realized that with his fearful exams he was simply doing what was needed: weeding out the students not fit for the demanding study course rather early, saving them and himself the pain of having to drag them along to an unsuccessful ending later.
The picture shows him going at full throttle in 1976, his last year of active teaching.

U. Dehlinger studied physics in Tübingen, München and Stuttgart, finishing with the degree of "Dipl.-Ing." in Technical Physics in 1923, and with the then very prestigious Dr.-Ing. in 1925.
In 1929 he applied for a "habilitation", a kind of second Dr. degree, necessary and qualifying for a professorship in Germany. In 1939 he became an "Ordinarius" (full professor) for Theoretical Physics at the "Technische Hochschule Stuttgart"; later University Stuttgart. .

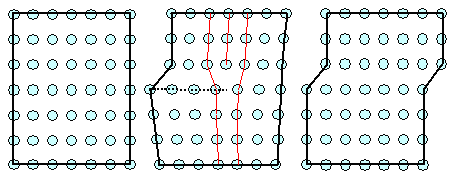
In the scientific work for this advanced degree he introduced the concept of "Verhakungen", a German construct that cannot be properly translated. It means something like "hooked together things" or "hookings". Dehlinger was a theoretician, albeit a practical one. It is important to realize that his "Verhakungen" were not a qualitative concept, just sketching possible crystal structures that might work in explaining something, but results of rather complex math applied to the problem of how whole collections of atoms could move in periodic structures like crystals. He enlarged on a concept earlier proposed by Prandtl , who considered what happens to the atoms in between two perfect crystalline regions with somewhat different orientations (a (small angle) grain boundary in modern terms). They would experience a periodic potential and, as Prandtl showed more or less qualitatively, could explain permanent deformations at low stress. Prandtl came close to the concept of imperfections or defects in crystals but did not get quite there. Here is the key picture oft Prandtl's model (redrawn and color added by me):


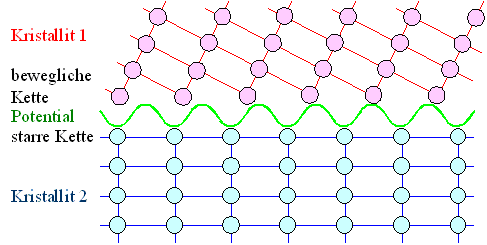Prandtl's Model (Bewegliche Kette = Movable chain, starre Kette = fixed chain)
Sources

Dehlinger, however, developed his model independently. He only became aware of Prandtl's work (which he acknowledged) after he had worked out his own ideas.

In contrast to Prandtl he considered the two crystallites being of the same orientation and worked out the details in complex and rigorous math. Here is his key picture of a "Verhakung" (redrawn and color added by me):


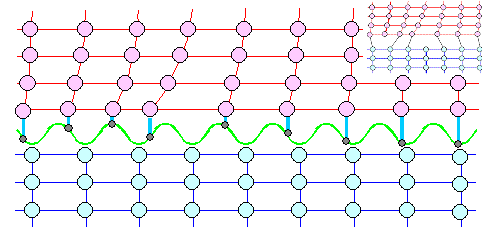Dehlinger' Verhakung

The green line shows the periodic potential used, and the blue lines indicate the energy of the atoms in the "Verhakung".
Not yet an edge dislocation but getting there. One could interpret this contraption as an edge dislocation dipole as shown in the inset but that wouldn't do justice to Dehlinger's intentions.

References:
Ulrich Dehlinger: Zur Theorie der Rekristallisation reiner Metalle. Habilitationsarbeit. Annalen der Physik (5) 2 (1929) 749-793.

Sir Peter Hirsch

When I worked the electron microscopes around 1975 in in A. Seeger's big Max-Planck Institute in Stuttgart, I knew Sir Peter the same way I knew the Pope. Well, Sir Peter, never seen in person by us little people, was the Pope as far as electron microscopy was concerned. Our own Boss, in this kind of idolatry, then was Martin Luther, challenging the Pope to the best of his ability but not really getting him down.


Sir Peter Hirsch * 16 January 1925

Hirsch's book about electron microscopy was (and to some extent still is) the Bible.

In 1946 Hirsch (not yet Sir Peter) worked under famous Lawrence Bragg for his PhD in the Crystallography Department of the Cavendish. In the mid-fifities he pioneered the application of transmission electron microscopy (TEM) and developed in detail the theory needed to interpret such images.
In 1966 he moved to Oxford to take up the Isaac Wolfson Chair in Metallurgy, succeeding William Hume-Rothery. He held this post until his retirement in 1992, building up the Department of Metallurgy (now the Department of Materials) into a world-renowned centre.

It was his group that saw a dislocation for the first time and knew what they saw. In Dec. 12th, 2002, he was interviewed at length about the development of Materials Science in the UK and elsewhere. Here are a few interesting quotes (my highlights and additions):

"By the time we found that cold worked aluminium breaks into subgrains, Heidenreich at the Bell Laboratories published the first pictures of metals by Transmission Electron Microscopy (TEM). He observed directly the little subgrains in heavily beaten aluminium foil. That depressed us very much because we needed exposures of many hours for our x-ray diffraction photographs, while he had a ten second exposure with his electron microscope. So we went into this field of TEM and finally we saw individual dislocations for the first time.
This had a big impact because there were many metallurgists who did not believe in dislocations, who considered them as figments of the imagination of solid state physicists working out theories in tremendous detail without much supporting experimental evidence. With our technique you could see dislocations directly and see them move. And we made movies. I remember showing a movie at MIT to Bert Warren who was a well-known X Ray crystallographer. His comment was symptomatic of many metallurgists. Seeing is believing. We converted people.

Finally would you consider yourself today more as a physicist or as a material scientist? "I think I am a physicist who «saw the light». True physicists would no longer consider me as a physicist. I consider myself as a materials scientist because my interest is in the effect of microstructure on the properties of materials. I am interested in quite complex materials, with potential applications e.g. high temperature intermetallics, and in modelling their complex mechanical properties. I ended up as a materials scientist. But there are materials scientists who would consider me to be a rather theoretical materials scientist. In the later years of my conversion I supported and promoted materials processing in the department although it took me rather a long time to get to this view, to appreciate the importance of this field, and to realize the need and potential for modelling."

You can read the story of the first dislocation picture in Sir Peter's own words in this link. To augment this, you can also read about the story from Michales Whelan, Hirsch's colleague and at least as involved in this as Hirsch.
Here is one of those first diffraction contrast pictures showing dislocations taken in a transmission electron microscope (TEM), a Siemens instrument at those heroic times:

$First diffraction contrast picture of dislocations$
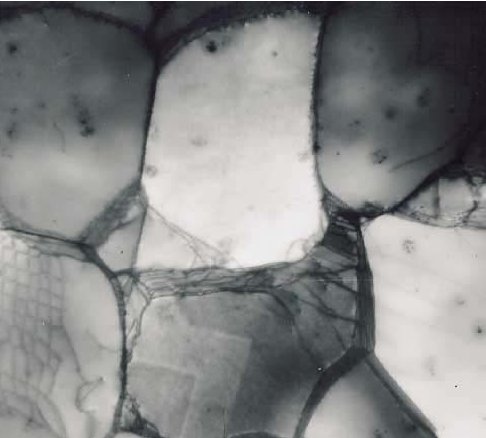First diffraction contrast TEM picture of dislocations
Prominent are the grains. The fainter lines, in particular the network on the lower left, are dislocations.
Source: Whelan interview

References:
P. Hirsch, A. Howie, R.B. Nicholson, D.W. Pashley and M.J. Whelan "Electron Microscopy of Thin Crystals", written in 1965
P. Hirsch; "50 Years of Transmission Electron Microscopy of Dislocations: Past, Present, and Future"; Herald of the Russian Academy of Sciences, 2006, Vol. 76, No. 5, pp. 430–436.
Address of interviews: http://authors.library.caltech.edu/5456/1/hrst.mit.edu/hrs/materials/public/Hirsch/Hirsch_interview.htm
http://authors.library.caltech.edu/5456/1/hrst.mit.edu/hrs/materials/public/Whelan/Whelan_interview.htm

Egon Orowan

Egon Orován was one of those many Hungarian scientists and artists¹⁾ who made the world a different place in the early 20th century.


Egon Orowan * Aug. 2nd, 1902 † Aug. 3rd, 1989
Source: Uni Cambridge. Museum

Orowan was born around Budapest. He started studying mechanical and electrical engineering at the Technical University of Berlin in 1928, but soon transferred to physics, completing his doctorate on the fracture of mica in 1932.

1937 Orowan moved to the University of Birmingham, UK where he worked on the theory of fatigue collaborating with Rudolf Peierls ; in 1939, he moved to the University of Cambridge where he worked with William Lawrence Bragg

During World War II, he worked on problems of munitions production, particularly that of plastic flow during rolling. In 1944, he was central to the reappraisal of the causes of the tragic loss of many Liberty ships, identifying the critical issues of the notch sensitivity of poor quality welds and the aggravating effects of the extreme low temperatures of the North Atlantic.

n 1950, Orowan moved to the Massachusetts Institute of Technology in Boston / USA. He made many more important contributions to dislocation science, applied fracture theory to geological and glaciological topics, and finally succumbed to that disease plaguing many elderly scientist (me included) and dabbled in philosophy, economy, and generally explaining the world at large.

He used, for example, the writings of some 14th century Tunisian historian Ibn Khaldun to forecast an eventual failure of markets. His ideas found little acceptance among the majority of economists, which might have been a mistake, considering that their ideas do no have much punch either (consider the various economic crises following each other in rapid succession right now).

Anyway, here is the front page of his paper:


Orowan's paper

Here are his decisive pictures (redrawn and color added by me):


Orowan's dislocation
Nowadays we would interpret it as a cut through a dislocation loop in a plane where the dislocation is purely edge type.

This picture is shown a lot in text books. The next picture, however, I have not seen before I consulted Orowan's original paper. It shows that Orowan did have a dislocation loop in mind, but didn't get it quite right because the screw dislocations hadn't been properly invented yet (even so it was implicitly contained in Volterra's work). Here is the picture (redrawn and color added by me):


Orowan's dislocation loop
The large pinkish circles denote the unchanged part of a crystal below the loop, the blue circles the slipped and undistorted part on top. The red circles show the distorted part in between

Orowan and Polanyi knew about each others work and actually made sure it was published together. Here is Orowan's reference to Polanyi:


Orowan's reference to Polanyi
"The transition zone between the glided and unmoved part of the plane, marked here by the additional stresses, is evidently identical to the dislocation described by P o l a n y i if seen from a lattice geometry viewpoint."

References:
Orowan E. "Zur Kristallplastizität. III. Über den Mechanismus des Gleitvorganges" (To crystal plasticity III. About the mechanism of glide), Z. Physik, 89 (1934) 634

Michael Polanyi

Mihály Polányi was born in Budapest in 1891 and is another member of those many Hungarian scientists and artists¹⁾ who made the world a different place in the early 20th century.


Michael Polanyi * March 11, 1891 † February 22, 1976
Source: Polanyi Society

After obtaining a medical diploma in 1914, he made it to the Technische Hochschule in Karlsruhe, Germany, to study chemistry. Peregrinations during the first World-War (as a medical officer) ended with a doctorate from the University of Budapest in 1919.
After a few more adventurous years he finally became the professorial head of department of the "Institut für Physikalische Chemie und Elektrochemie" in Karlsruhe.
Forced out by the Nazis, he moved to the University of Manchester. Two of his pupils, Eugene Wigner and Melvin Calvin, not to mention his own son, went on to win a Nobel Prize.

Polanyi's scientific interests were extremely diverse, including work in chemical kinetics, x-ray diffraction, and the adsorption of gases at solid surfaces. In 1934 he realized that the plastic deformation of ductile materials could be explained in terms of what we now call a dislocation.

In later life he became a philosopher, like Orowan. In contrast to Orowan he received some recognition for this work to this very day.

Here is his decisive picture (redrawn and color added by me):


Polanyi's dislocation

Here is Polanyi's opening page:


Polanyi's paper

The abstract of his paper (red lines ) simply states:
"If there is a lattice dislocation in a slip plane, with n atoms on the one coast opposed to n + 1 atoms on the other coast, the resistance to shear along the glide plane will be weakened to about 1/n.".
The idea is correct but the statement is not.
The footnote (blue lines) contains his reference to Orowan. It reads:
"The communication "Zur Kristallplastizität" (to crystal plasticity) of E. Orowan contained in this volume induced me to publish these notes made some time ago. The proof of E. Orowan, that glide issues from nuclei spontaneously generated in a crystal, appears to me to be an important step in the elucidation of plasticity, justifying to some extent the following thoughts.

Polanyi also refers to the work of Taylor, Prandtl and Dehlinger:


Polanyi's reference to Taylor, Prandtl and Dehlinger.

References:
M. Polanyi, "Über eine Art Gitterstörung, die einen Kristall plastisch machen könnte" (About a kind of lattice distortion that could render a crystal "plastic" (= ductile) ), Z. Physik, 89 (1934) 660

Geoffrey Ingram Taylor

Geoffrey Ingram Taylor (affectionately known as G. I.) was a very British mathematician and physicist with a focus on hydrodynamics (like Prandtl or Burgers) and made quite a name for himself in that discipline.


* March 7th. 1886 † Jun 27th 1976

During the first World War he was sent to the Royal Aircraft Factory at Farnborough and did theoretical work, e.g. on the stress on propeller shafts. Not so theoretical, he also earned to fly aeroplanes and to parachute.

in 1923 he was appointed to a Royal Society research professorship as a Yarrow Research Professor in Oxford. This enabled him to stop teaching, which he neither liked nor could do very well.
It was in this period that he did his most wide-ranging work on the mechanics of fluids but also, following up his work at Farnboroug, in solids. This lead to his "discovery" of the (edge) dislocation in 1934. In 1934. Taylor also realized that the theory of "dislocations" as developed by Vito Volterra in 1905 was instrumental for this.

He did not succumb to the lure of "philosophy" as his two dislocation co-inventors but had botany as a hobby and sailing as a kind of obsession. Once more he became practical and invented and patented a special kind of anchor. His final research paper was published in 1969, when he was 83. In it he resumed his interest in electrical activity in thunderstorms, as jets of conducting liquid motivated by electrical fields

Here is his decisive picture (redrawn; color and the red lines added by me):


Taylor's (positive) dislocation The second picture of the "negative dislocation is essentially the same picture just standing on its head.
This looks not only very much like a classical edge dislocation, it also shows how plastic deformation comes about by the movement of the dislocation. Here is the text to this picture

The Royal Society expects, of course, that publications in its august journal are always read from the beginning to the end and thus supplies no abstract. Instead of the beginning of the article I therefore show the parts referring to Dehlinger and Volterra:


Taylor's reference to Dehlinger


Taylor's reference to Volterra

Taylor's paper - with a part I and a part II - is 53 pages long and goes deep into theory and math. It certainly would have been sufficient to establish the dislocation once and for all.

References:
G. I. Taylor, "The mechanisms of plastic deformation of crystals. Part I—Theoretical; Part II—Comparison with Observation; Proc. Royal Soc. Series A, Vol CXLV (=145) (1934) p. 362 - 415

Vito Volterra

Vito Volterra was an Italian mathematician and physicist. He was and is far more famous for his contributions to mathematical biology and integral equations than to dislocation science.
Born in Ancona, then part of the Papal States, into a very poor Jewish family, Volterra showed early promise in mathematics before attending the University of Pisa, where he became professor of rational mechanics in 1883. In 1892, he became professor of mechanics at the University of Turin and then, in 1900, professor of mathematical physics at the University of Rome La Sapienza.


Vito Volterra * May 3rd, 1860 † Oct. 11th 1940
Source: The Net at large

In recognition of his scientific achievements, Volterra was made a senator of the kingdom of Italy in 1905. But in 1931 he was one of only 12 out of 1,250 professors who refused to take a mandatory oath of loyalty to the fascist regime. As a result, he was compelled to resign his university post and his membership of scientific academies, and, during the following years, he lived largely abroad, returning to Rome just before his death.

His work, I read in biographies, is summarized in his book "Theory of functionals and of Integral and Integro-Differential Equations (1930)"
Indeed, it is hard to find general references to his work relevant for dislocations.

What he did was to propose a new theory of elastic distortions . On the surface, it is outrageously simple. He took a hollow tube, cut it lengthwise, and considered how you can "glue" it together again (removing or inserting material if necessary), and what kinds of stress and strain fields would result. Note that his material was continuous mathematical "brain" matter. There were no atoms and hence no crystals involved.
The six possibilities he came up with are shown in the figure below:


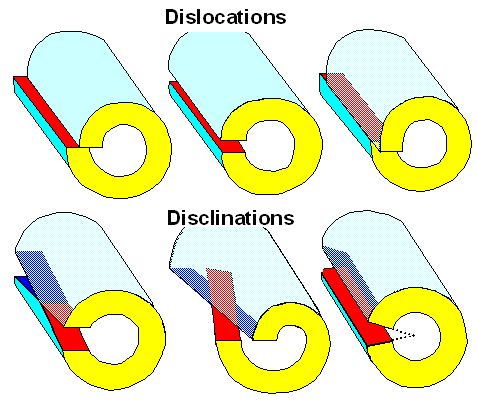Volterra's six essential "cut and glue" constructs.

If it is not directly obvious to you that this is a work of genius, try to prove rigorously that there are no other possibilities of deforming matter that cannot be constructed by applying one or more of the six above. Mathematicians have far more to say about things like that, all of which is incomprehensible to normal people including me.

You realize, of course, that in a crystal lattice the upper row shows two edge dislocations and a screw dislocation.
The lower row is also interesting. Applied to lattices it shows a possible elementary defect called "disclination" that is, however, almost never observed in three-dimensional crystals - but in two dimensional periodic structures.

References:
V. Volterra, “Sulle distorsioni dei corpi elastici simmetrici,” Rend. Accad. Lincei, vol. 14, 1905. V. Volterra, L'equilibre des corps élastique multiplement connexes, Gauthier-Villars, Imprimeur-libraire, Paris, France, 1907.



¹⁾	I'm just back from an operetta gala performed in the Kiel opera with stars from, e.g., the New York City Metropolitan - did I mention already that Germany has far more full-grown operas (84) than any other country? My wife and I were fabulously entertained. Music from two Hungarian composers was played, inspiring me to give you the following short list of Hungarian scientists and artists who made the world a different place in the early 20th century. Of course, many of these names go back to Austro-Hungarian times, and that's why many of these persons wrote their things in German. I only included names that even "normal" people might recognize. This implies that "our" Hungarians from above, plus more than hundred others, are not listed!
	Theodore Herzl (Herzl Tivadar, 1860 - 1904), spiritual founder of Israel . Joseph Pulitzer, 1847 - 1911, newspaper publisher. László Bíró, 1899 -1985, inventor of the ballpoint pen. Andrew Grove (András Gróf, 1936 -), pioneer of the semiconductor industry, CEO of Intel. Rudolf (Rudy) Emil Kálmán, (1930 -), inventor of the Kalman filter know to all (electrical) engineers Eugene Wigner (Wigner Jeno, 1902 -1995), physicist; Nobel prize 1963 Dennis Gabor (Gábor Dénes,1900 - 19 71), inventor of holography, physics Nobel prize 1971. John Charles Polanyi (Polányi János 1929 -), chemist; son of " our" Polanyi here; Noble prize 1986. Elie Wiesel (1928 - 1986). Peace Noble prize 1986 John von Neumann (1903 – 1957). Extremely famous mathematician. Theodore von Kármán (Szolloskislaki Kármán Tódor, 1881 – 1963), very famous physicist. Leó Szilárd (Szilárd Leó, 1898 – 1964). Physicist and inventor who conceived the nuclear chain reaction in 1933, patented the idea of a nuclear reactor with Enrico Fermi, and in late 1939 wrote the letter for Albert Einstein's signature that resulted in the Manhattan Project that built the atomic bomb. He also conceived the electron microscope. Edward Teller (Teller Ede,1908 – 2003). Physicist, known colloquially as "the father of the hydrogen bomb". Paul Abraham (Pál Ábrahám 1892 - 1960). Composer of operettas, e.g. "Viktoria und ihr Husar", "Die Blume von Hawaii". Emmerich (or Imre) Kálmán (1882 – 1953). Composer of operettas, e.g. "Die Csárdásfürstin", "Gräfin Mariza", or "Die Zirkusprinzessin". Sir Georg Solti, (1912 – 1997). Conductor . Incidentially, the list of famous jewish Hungarians is pretty much identical to the list of famous Hungarians.

¹⁾

Ludwig Prandtl: Ein Gedankenmodell zur kinetischen Theorie der festen Körper. Zeitschrift für angewandte Mathematik und Mechanik 8 (1928) 85-106.
Theodor von Kármán: Physikalische Grundlage der Festigkeitslehre. Encyclopädie der mathematischen Wissenschaften. Teubner, Leipzig (1907-1914). Bd.IV, 4, (1913) 695-770. Kármán new about Prandtls' model and discusse in this paper long before Prandtl published it himself.
Markus Heyerhoff, Dissertation, Greifswald 1997
A. K Seeger, Early work on dislocations and forerunners of dislocation theory, Proc. R..Soc. Lond. A371 (1981) 173 - 177

With frame