5.3.3 Real Heterojunctions

Misfit Dislocations and Critical Thickness

So far we considered ideal heterojunctions. What do we mean with ideal? You can look at it in two ways

The junction is structurally ideal, i.e. you just switch from one set of atoms on one side of the junction to another set on the other side. For that you need the same type of crystal lattice and identical, or at least very similar lattice constant, of course.

The junction is electronically ideal, i.e. the interface does not have any interface states in the band gap (in analogy to the case of a free surface treated before) or is otherwise interfering with carrier densities and transport.

But even for these ideal conditions we have an energy discontinuity at the interface with a charged dipole layer if the badgap energies are different. What happens for real interfaces, the only ones we can actually make?

Real interfaces have one thing in common: The lattice constants of the two materials joined at the interface are never precisely identical. And from this fact of life evolve many problems – and many ingenious technologies to avoid those problems.

The basic problem is the same for all heterojunctions. The lattice misfit between the two crystal may cause the incorporation of a network of so-called misfit dislocations into the interface. And this misfit dislocation network is the source of practically all evil in heterojunctions – if you have it, your device will not work at all, will work only badly, or fail after some (too short) time.

Compared to the "high physics" part of the electronic and quantum properties of heterojunctions, this looks like a mundane problem. Well, it is – but it is here where most grandiose ideas for stunning devices go down the drain. If you can not make the junction, you won't get far with your device.

If you are especially interested in this topic, or if you only have a very dim perception of lattice defects in general and dislocations in particular, you should now turn to the hyperscript "Defects in Crystals" either in general, or to the chapters "Dislocations" or "Phase boundaries" in particular; here we only will deal with the very basics of misfit dislocations.

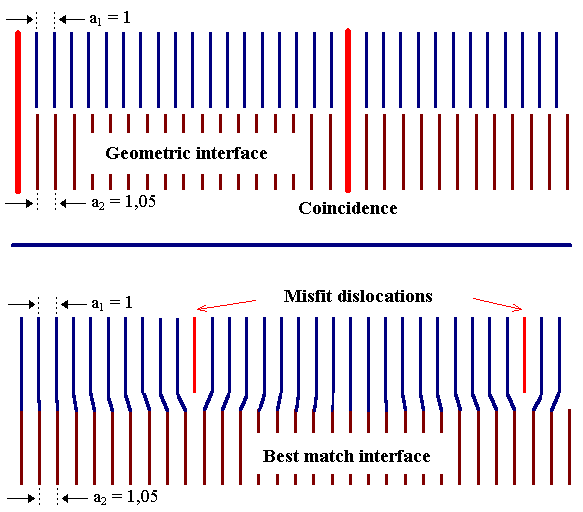
The following figure shows what misfit dislocations are and why they are formed.

If you just geometrically juxtapose two crystals, you will have a situation as shown in the upper part for a misfit of 5%.

Only every 20th lattice point will precisely match between the two lattices (at so-called coincidence sites). In between, the situation does not only look highly instable, but really is unstable. If there is any appreciable interaction between the atoms of lattice 1 and lattice 2, something will happen and that is almost always the case (mother nature, of course, does provide some exotic crystals with "geometric" interfaces as the exception).

Other weird solutions are conceivable, e.g. an amorphous layer between the two crystals, some highly disordered region formed by a mixture of the two lattices – you name it. While all of this does happen on occasion, it is not the rule; certainly not for "normal" semiconductors.

Eschewing "geometric" and "weird" interfaces, there are only two reasonable options left:

1. The lattices are elastically squeezed or expanded until they fit precisely. The amount of energy contained in the necessary elastic distortions is directly proportional to the volume of the deformed material; for the one-dimensional structures we are usually envisioning, the energy scales with the thickness of the layers.

2. Misfit dislocations are introduced as shown above. This means that all the misfit is concentrated in a small volume around the dislocations, while in between we have a perfect fit with only a little elastic distortion. The total energy contained in the distortion around the dislocations is rather large, but does not depend much on the volume (resp. thickness) of the crystals.

As a simple and sad consequence we then have the following basic fact of life:

For layer thicknesses larger than some system-dependent critical thickness d_crit, the introduction of a misfit dislocation network is always energetically favorable.

Deriving a formula for the critical thickness is not without problems and some material specific idiosyncrasies, but in general we have

d_crit =	b 8 · p · f · (1 + n )	· ln	e · d_crit r₀

With b = Burgers vector of the dislocations; usually somewhat smaller than a lattice constant, f = misfit parameter = (a₁ – a₂)/a₁, n = Poisson ration » 0.4,
e = base of natural logarithms = 2.718..., r₀ = inner core radius of the dislocation; again in the order of lattice constant.

Getting precise values of d_crit is such not easy (not to mention that the equation above has no analytical solution); but for a crude approximation that can be used for "normal" cases we simply have

d_crit	=	b 10 · f

More about that can be found in an advanced module.

If, for example, we look at the system GaAs/InAs , we have lattice constants of 0.565 and 0.606 nm, so f = 0.0726 (i.e. the misfit is 7.2 %). The Burgers vectors in these crystals are usually a /(2^1/2) » 0.42nm, which gives us a critical layer thickness of d_crit = 0.58 nm – less than 2 crystal layers. ¹⁾

Shit (really)! This looks not so good – and in fact, nobody uses the GaAs/InAs system for heterojunctions. But we have better couples, especially mother natures gift to optoelectronics, the GaAs/AlAs system and the InAs/GaSb/AlSb system where the misfit parameters are much smaller.

If we go through the numbers for GaAs/AlAs with 0.5653/0.5660, we obtain d _crit = 57 nm – a value sufficient for many applications.

While this is nice, we must of course ask ourselves if there are ways to beat the d_crit equation, i.e., to produce layers with a thickness larger than the critical thickness. This is indeed the case and we will look at some of the methods to produce dislocation free heterojunctions despite the energetic limitations. More about misfit dislocations (and other problems in heterojunctions) can be found in an advanced module.

Extending the Critical Thickness

There are some ways to beat the critical thickness to a smaller or larger extent; we will just give them a cursory glance which will not do justice to the sweat and toil as well as hard thinking that went into this problem.

First , do not believe the theory and give up because it looks bad.

Even the full equation from above does not take all parameters into account. The situation may be better (or worse) than the numbers you obtain.

Try it experimentally, at least as the layer thickness you need is not too far (at least a factor 3 or more) above the theoretical limit. You might be lucky!

However, don't try for really large misfits above, say, 2 %. Not only is the critical thickness small, but you probably will not even be able to obtain a smooth layer – islands will grow!

Second, consider the kinetics of the layer deposition process.

Any formula for d_crit (including much more advanced treatments) is an equilibrium formula, comparing enthalpies in equilibrium.

However, since your layer thickness always is below d_crit at the beginning of the deposition process, there are no misfit dislocations in the beginning of the deposition. After the critical thickness is reached, dislocations must be nucleated and move from the surface to the interface and this is a kinetic process which you may be able to impede.

In other words, for optimized conditions, you may obtain dislocation free interfaces for kinetic reasons. In particular, make the nucleation of dislocations difficult by avoiding all irregularities (including temperature gradients) that may serve as nuclei.

Third, minimize the elastic strain energy by using a buffer layer.

This is maybe the most important trick; especially if you want to produce many junctions for multiple quantum wells.

Lets look, e.g., at a MQW sequence consisting of the substrate material (yellow) and a material with a larger lattice constant (blue) very schematically before the "joining" of the crystals. Keep in mind that the substrate, being very thick, never "gives" – only the layers will be strained!

Even if the first blue layer is below the critical thickness, the stress will build up, and after a few layers you have misfit dislocations for sure (left part of the figure).

The break-through came with the introduction of a buffer layer in which the lattice constant is gradually changed (by gradually changing the composition) to a value halfway in between material 1 and material 2. This is shown in the right part of the figure. The effect is that while the stress in the layers is about the same as before, it does not build up anymore with the number of layers if everything is done just right – multiple quantum wells are possible!

In reality, the buffer layer is much thicker so it cannot be strained very much as shown.

Buffer layers of some mysterious kind, it seems, also finally helped to obtain the holy grail of heteroepitaxy: Growing GaAs on Si without misfit dislocations.

Not an easy task, if you consider that the misfit is about 4.1 %. Still, Motorola appears to have solved the problem, if you can believe newspaper articles. The "appears" relates to what you actually read in one of Germanys finest daily; the article is contained in the link – click on it and try if you can make some sense out of it (provided you understand German). Otherwise try this link.

Fourth, accept the misfit dislocations, but put them in a part of the system where they do no harm.

This approach is known under the heading "compliant substrates". The basic idea is simple (and illustrated in an advanced module): Make a bicrystal (usually of Si) by bonding two wafers together with a defined twist of up to 15° along the axis perpendicular to the wafer. A grain boundary ("small-angle twist boundary") must form, consisting of a dense array of screw dislocations.

Now polish off one of the Si wafers until only a thin layer (1 µm or less) remains. This does not only sound difficult to do, it really is – but nevertheless it can be done in a large scale production. The remaining sandwich, thick Si / grain boundary / thin Si, is your compliant substrate.

If you now deposit a layer of anything on thin Si layer, any misfit (up to very large amounts) between the thin Si layer and the deposited layer of the other material will be accommodated by the dislocations in the grain boundary – there is no need to form new ones.

The important interface thus remains dislocation free and you may now be able to do things not possible so far.

__________________________

¹⁾

Note that in contrast to the elemental diamond lattice, where the smallest possible Burgers vector for a perfect dislocation is b_elem = a/(2 · 2^1/2), we have b_comp = a/(2^1/2 ) because we would otherwise replace A-atoms by B-atoms in the glide plane of the dislocations (look at the Volterra "cut and paste" definition of a dislocation in the "Defects in Crystals" hyperscript).